Содержание
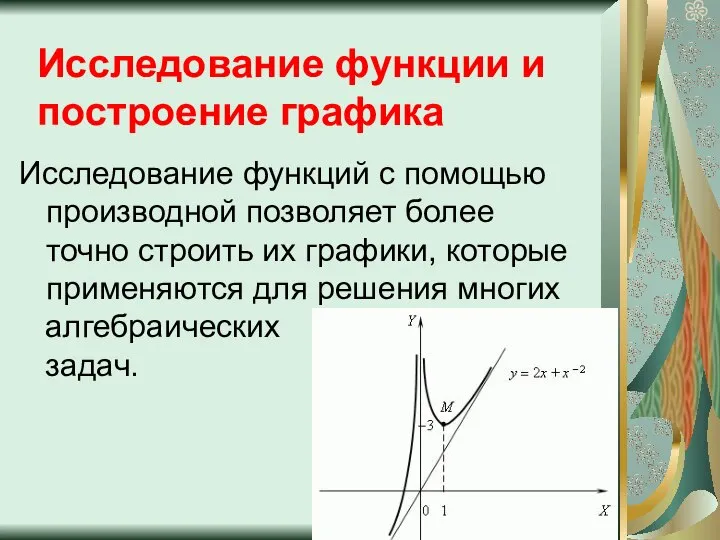
- 2. Исследование функций с помощью производной позволяет более точно строить их графики, которые применяются для решения многих
- 3. Схема исследования функции Область определения Чётность, нечётность Периодичность Точки пересечения графика с осями координат Промежутки знакопостоянства
- 4. Область определения функции Множество всех значений аргумента, при котором функция определена. D(f)
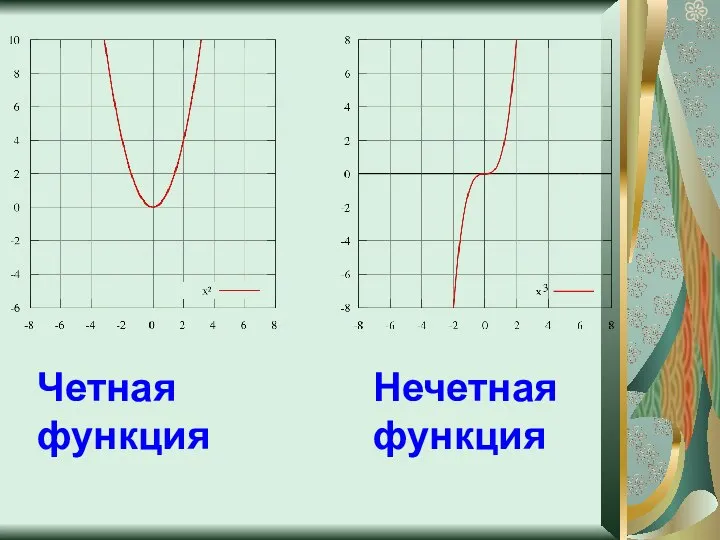
- 5. Чётность, нечётность D(f)-симметрична относительно О(0;0). Если f(-x)=f(x)-функция четная. Если f(-x)=-f(x)-функция нечетная. Если функция ни та, и
- 6. Четная функция Нечетная функция
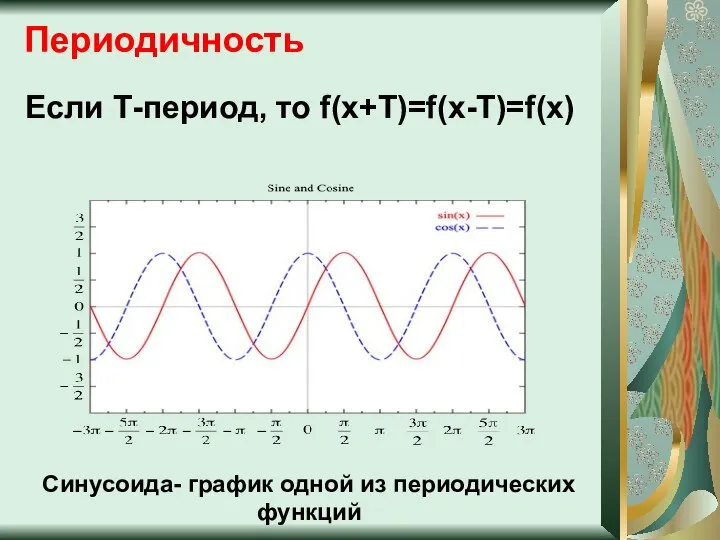
- 7. Периодичность Если Т-период, то f(x+T)=f(x-T)=f(x) Синусоида- график одной из периодических функций
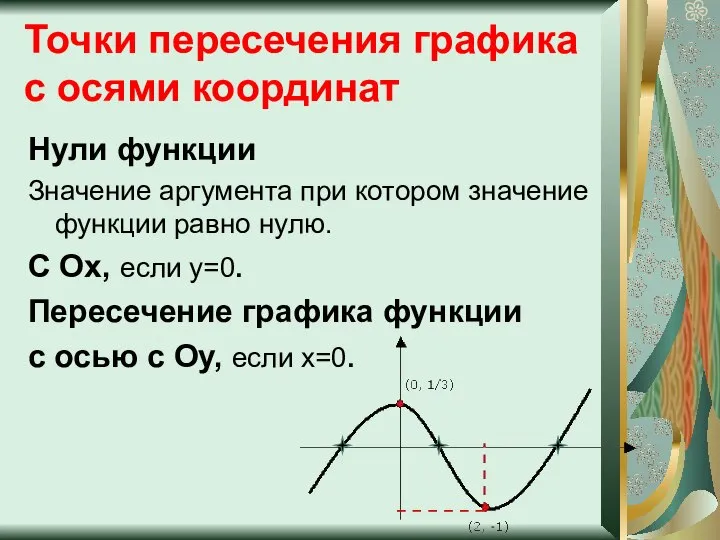
- 8. Точки пересечения графика с осями координат Нули функции Значение аргумента при котором значение функции равно нулю.
- 9. Промежутки знакопостоянства Промежутки знакопостоянства – интервалы, на которых функция положительна или отрицательна, или, иначе, решения неравенств
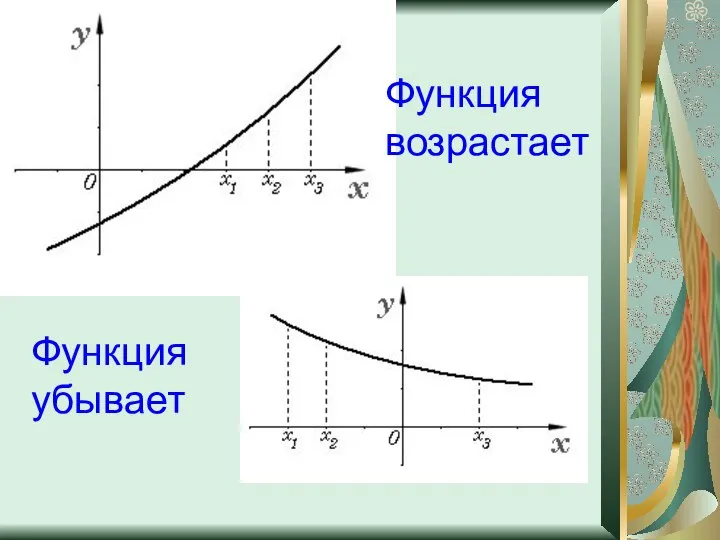
- 10. Монотонность Функция f (x) называется возрастающей на промежутке D, если для любых чисел x1 и x2
- 11. Функция возрастает Функция убывает
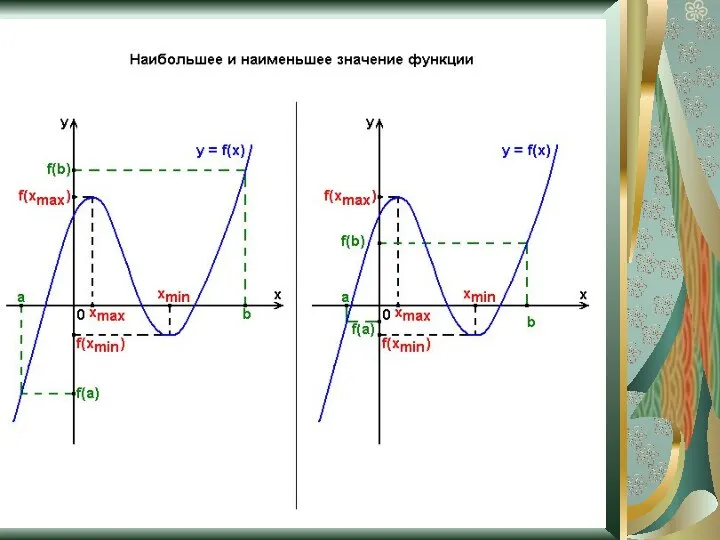
- 12. Экстремумы Точки экстремума – точки, лежащие внутри области определения, в которых функция принимает самое большое (максимум)
- 13. Множество значений функции Наибольшее и наименьшее значение Множество значений функции – множество чисел, состоящее из всех
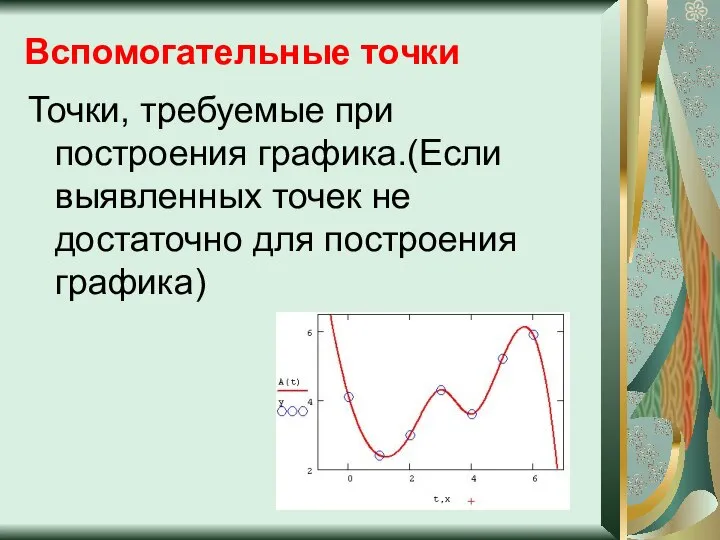
- 15. Вспомогательные точки Точки, требуемые при построения графика.(Если выявленных точек не достаточно для построения графика)
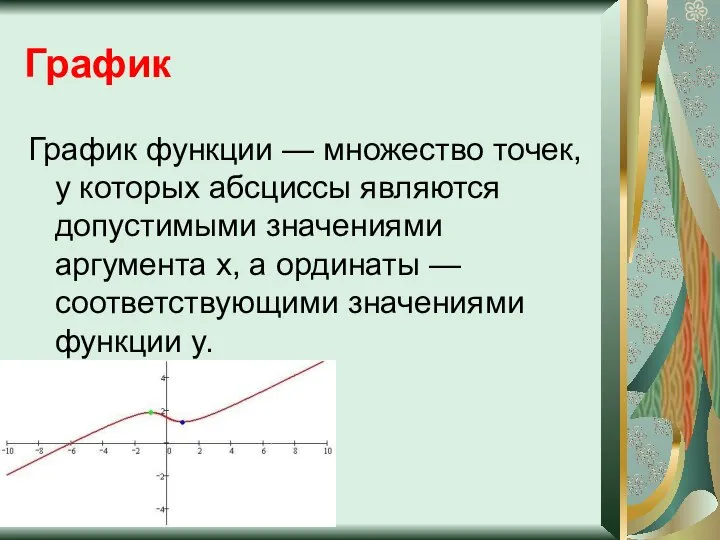
- 16. График График функции — множество точек, у которых абсциссы являются допустимыми значениями аргумента x, а ординаты
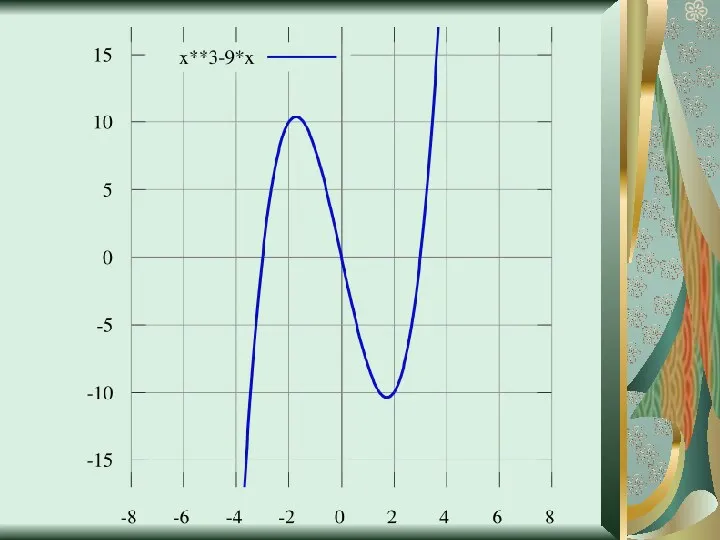
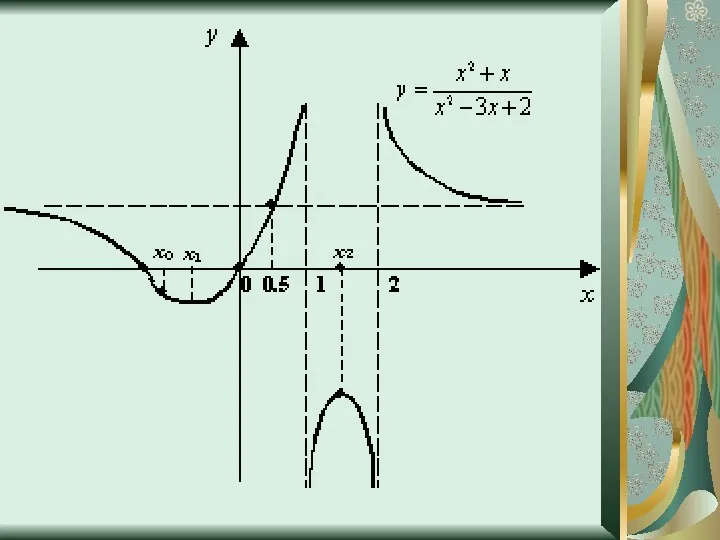
- 18. Исследование функции y=(x2+x)/(x2-3x+2) Упростим выражение y=(x2+x)/(x2-3x+2); y=(x2+x)/((x-1)*(x-2)) D(f)=R\1,2 Функция общего вида, т.к.f(-x)≠f(x) и f(-x)≠ -f(x) Непериодическая
- 19. Промежутки знакопостоянства Находим производную функции y’=(-4x2+4x+2)/((x-1)2*(x-2)2) D(f’)=R\1;2 Находим промежутки возрастания и убывания функции (-4x2+4x+2)/((x-1)2*(x-2)2)=0 -4x2+4x+2=0 x1=
- 20. Экстремумы x= (-1+√3)/-2 -точка минимума; y((-1+√3)/-2)=(2-2√3)/(3+2√3) x= (-1-√3)/-2-точка максимума; y((-1+-√3)/-2)=(2+2√3)/(3-2√3) 9. E(y)=(-∞;(2-2√3)/(3+2√3)U(2+2√3)/(3-2√3);+∞) 10. График
- 23. Скачать презентацию










 Арифметический квадратный корень. Задания для устного счета. 8 класс
Арифметический квадратный корень. Задания для устного счета. 8 класс Преобразование графика тригонометрической функции у = sin x путем сжатия и расширения
Преобразование графика тригонометрической функции у = sin x путем сжатия и расширения Тела гладкие. Тела складчатые
Тела гладкие. Тела складчатые Решение практических задач по теме: «Первый признак равенства треугольников»
Решение практических задач по теме: «Первый признак равенства треугольников» Урок–путешествие в страну «Дроби»
Урок–путешествие в страну «Дроби» Круговая окружность
Круговая окружность Выполнили: обучающиеся 8 класса НОУ СОШ “Вайда” Полякова Елизавета, Третьякова Ольга
Выполнили: обучающиеся 8 класса НОУ СОШ “Вайда” Полякова Елизавета, Третьякова Ольга  Тригонометрические уравнения
Тригонометрические уравнения Удивительные десятичные дроби. 5 класс
Удивительные десятичные дроби. 5 класс Примеры экзаменационных заданий по теме Числа и вычисления
Примеры экзаменационных заданий по теме Числа и вычисления Таблица умножения и деления на 7. Тренажёр
Таблица умножения и деления на 7. Тренажёр Помогают законы. 5 - 7 класс
Помогают законы. 5 - 7 класс Основы теории переключательных функций
Основы теории переключательных функций Теорема Пифагора (теорема нимфы, теорема невесты)
Теорема Пифагора (теорема нимфы, теорема невесты) Производная. Правила вычисления производных
Производная. Правила вычисления производных Функции и их графики. 9 класс
Функции и их графики. 9 класс Длина окружности и площадь круга
Длина окружности и площадь круга Случайные процессы общего вида
Случайные процессы общего вида Сложение и вычитание десятичных дробей. Задачи про олимпийские виды спорта
Сложение и вычитание десятичных дробей. Задачи про олимпийские виды спорта Задачи на готовых чертежах. Четырехугольники
Задачи на готовых чертежах. Четырехугольники Поверхности вращения
Поверхности вращения Презентация по математике "Сравнение чисел. Графы" - скачать бесплатно
Презентация по математике "Сравнение чисел. Графы" - скачать бесплатно 6 класс
6 класс  Проверка статистических гипотез
Проверка статистических гипотез Статистическое изучение взаимосвязей
Статистическое изучение взаимосвязей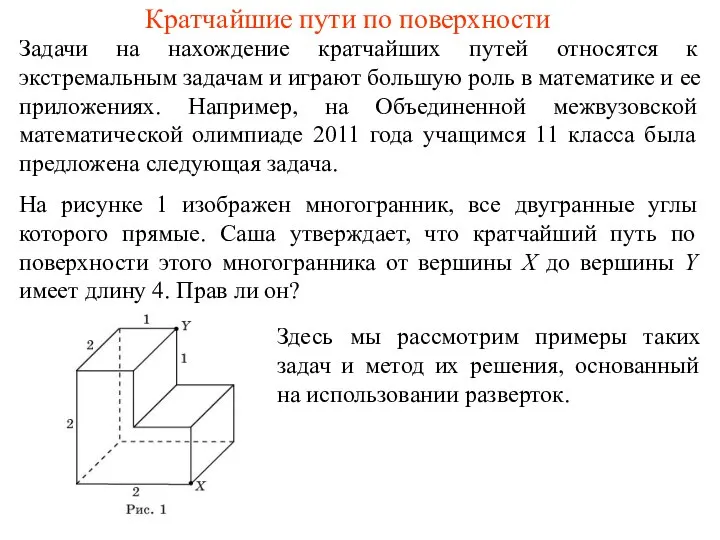 Кратчайшие пути на поверхности
Кратчайшие пути на поверхности Решение задач. Площадь треугольника
Решение задач. Площадь треугольника Статистическое изучение взаимосвязи социальноэкономических явлений
Статистическое изучение взаимосвязи социальноэкономических явлений