Содержание
- 2. Определение числового ряда Сумма ряда Примеры числовых рядов Определение частичной суммы Сходящиеся и расходящиеся ряды Признак
- 3. Еще в древности ученые встречались с понятием бесконечных последовательностей: U1, u2, u3, un, …, и с
- 4. u1, u2 , u3, …, un, … s1, s2 , s3, …, sn, … , где
- 5. Сходящиеся и расходящиеся ряды. Ряд называется сходящимся, если последовательность его частичных сумм имеет конечный предел Этот
- 6. Пример 1. Выражение 1 + (-1) + 1 + (-1) + … + (-1)n+1 + …
- 7. Пример 2. Выражение является рядом. Из членов составляют частичные суммы Примеры числовых рядов.
- 8. Пример 3. Ряд 1 + 2 + 3 + 4 + … + n + …
- 9. Пример 4. Ряд 1 – 1 + 1 – 1+ … +(-1)n+1 + … - расходящийся,
- 10. Поэтому Исследование на сходимость.
- 11. Ряд u1 + u2 + … + un + … может сходится, когда общий член ряда
- 12. Пример 5. Ряд 0,4 + 0,44 + 0,444 + 0,4444 + … - расходится, т.к. общий
- 13. Сумма ряда. Если знаменатель прогрессии удовлетворяет неравенству: |q| то последовательность частичных сумм (Sn) имеет предел: который
- 14. Признак Даламбера Если члены положительного ряда а1+а2+ …+ аn+… таковы, что существует , то при ряд
- 15. Применение признака Даламбера Примеры Исследовать на сходимость следующие ряды: 1. 2. Решение: воспользуемся признаком Даламбера: ряд
- 16. Применение признака Даламбера Решение второго примера: т.к. , то ряд расходится.
- 17. Леонард Эйлер (1707-1783) Швейцарский математик и механик, академик Петербургской Академии наук, автор огромного количества научных открытий
- 18. Краткая историческая справка Жан Лерон Даламбер получил своё имя по названию маленькой церкви на ступени которой
- 19. Краткая историческая справка Однако сенсуализм его не был последовательно материалистическим. По Даламберу, мышление не является свойством
- 20. Использованная литература. И. И. Баврин, В. Л. Матросов «Общий курс высшей математики» Москва, 1995; А. Г.
- 22. Скачать презентацию








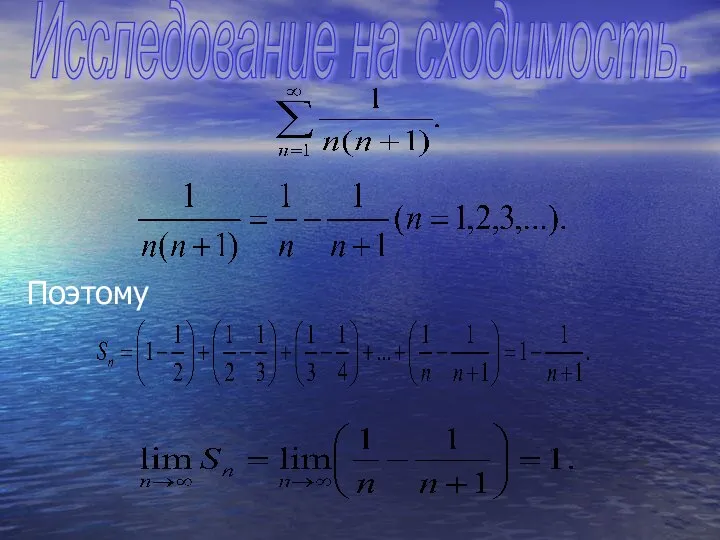










 Степенная функция
Степенная функция Показательные неравенства
Показательные неравенства Обыкновенные дроби и действия с ними
Обыкновенные дроби и действия с ними Тест. Задания В12, ЕГЭ по математике
Тест. Задания В12, ЕГЭ по математике Применение симметрии при решении алгебраических задач Учениц 10И класса: Коротковой Анастасии Журавлёвой Дарьи Руководитель:
Применение симметрии при решении алгебраических задач Учениц 10И класса: Коротковой Анастасии Журавлёвой Дарьи Руководитель:  Сіткове і календарне планування проекту
Сіткове і календарне планування проекту Отрезок
Отрезок Ух, уж эта математика
Ух, уж эта математика Задачи на работу. 9 класс
Задачи на работу. 9 класс Система m линейных уравнений с n неизвестными
Система m линейных уравнений с n неизвестными Теория графов. Его величество граф
Теория графов. Его величество граф Изучение таблицы умножения в разных странах
Изучение таблицы умножения в разных странах Презентация по математике "Приемы устного умножения и деления" - скачать
Презентация по математике "Приемы устного умножения и деления" - скачать  Положительные и отрицательные числа
Положительные и отрицательные числа Иррациональные уравнения и неравенства
Иррациональные уравнения и неравенства Определение арифметической прогрессии
Определение арифметической прогрессии Урок-презентация Урок-презентация «Сложение и вычитание десятичных дробей».
Урок-презентация Урок-презентация «Сложение и вычитание десятичных дробей». Десятичные дроби. Путешествие на математическом поезде
Десятичные дроби. Путешествие на математическом поезде Квадратные неравенства. Решение примеров. 9 класс
Квадратные неравенства. Решение примеров. 9 класс Основное свойство дроби
Основное свойство дроби Внеклассное мероприятие «Что? Где? Когда» в 9 – 11 классах
Внеклассное мероприятие «Что? Где? Когда» в 9 – 11 классах Грегор Мендель Закон единообразия гибридов Закон расщепления признаков
Грегор Мендель Закон единообразия гибридов Закон расщепления признаков Математика учит точности мысли
Математика учит точности мысли Комбинаторика. Комбинаторные задачи
Комбинаторика. Комбинаторные задачи Оформление краткой записи задачи 1-2 классы
Оформление краткой записи задачи 1-2 классы Элементы математической логики. Формулы алгебры логики
Элементы математической логики. Формулы алгебры логики Достроить недостающие проекции отрезка АВ. (задача 13)
Достроить недостающие проекции отрезка АВ. (задача 13) Готовимся к ЕГЭ. Задача С2. Задачи, где присутствует построение сечения
Готовимся к ЕГЭ. Задача С2. Задачи, где присутствует построение сечения