Содержание
- 2. Система m линейных уравнений с n переменными имеет вид
- 3. Любые m переменных системы m линейных уравнений с n переменными (m Тогда остальные n - m
- 4. Базисным решением системы m линейных уравнений с n переменными называется решение, в котором все n-m неосновных
- 5. Геометрический метод решения задач линейного программирования
- 6. Решение неравенств
- 7. Множеством решений неравенства с двумя переменными является одна из полуплоскостей, на которые вся плоскость делится прямой
- 9. Множеством решений совместной системы m линейных неравенств с двумя переменными
- 10. является выпуклый многоугольник (или выпуклая многоугольная область)
- 11. Множество всех допустимых решений совместной системы m линейных уравнений с n переменными (m
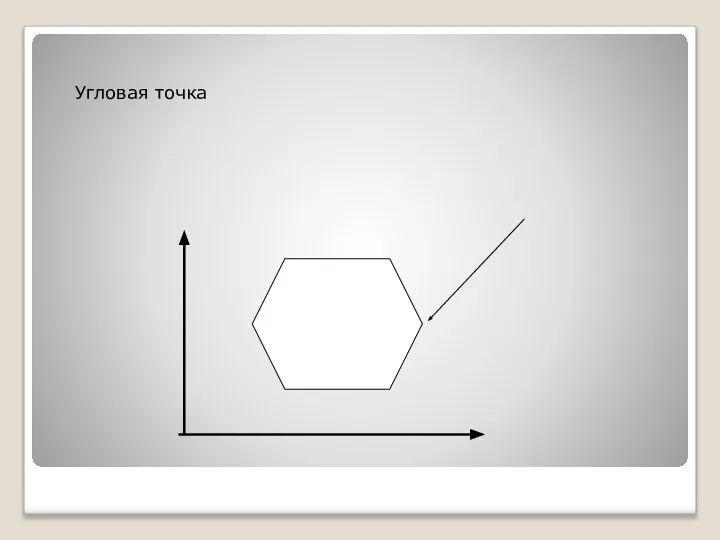
- 12. Угловая точка
- 13. Сформулированные теоремы и понятия позволяют сделать следующие выводы.
- 14. Если основная задача линейного программирования имеет оптимальный план, то максимальное или минимальное значение целевая функция задачи
- 15. Если максимальное значение целевая функция задачи принимает более чем в одной вершине, то она принимает его
- 16. Для определения этой вершины необходимо построить линию уровня c1x1+ c2x2=h (где h – некоторая постоянная), проходящую
- 17. и будем передвигать ее в направлении вектора d= (c1;c2), до тех пор, пока она не пройдет
- 18. Координаты указанной точки и определяют оптимальный план данной задачи.
- 19. Заканчивая рассмотрение геометрической интерпретации задачи , отметим, что при нахождении ее решения могут встретиться случаи, изображенные
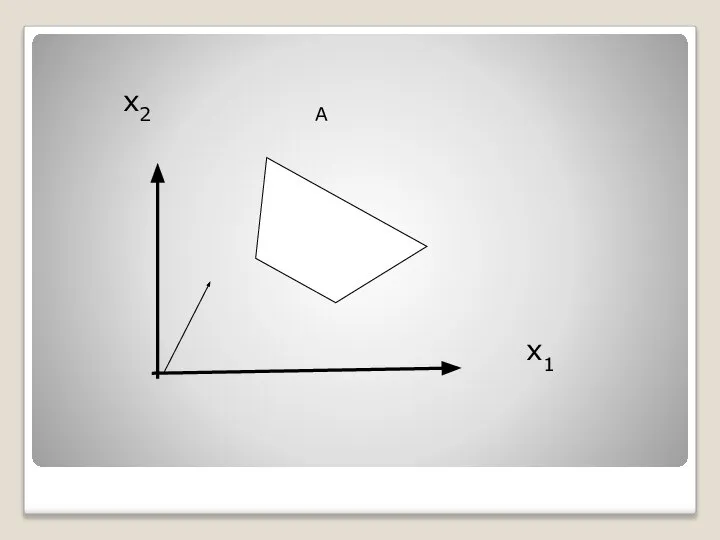
- 20. Рис. 1 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке А.
- 21. х2 А х1
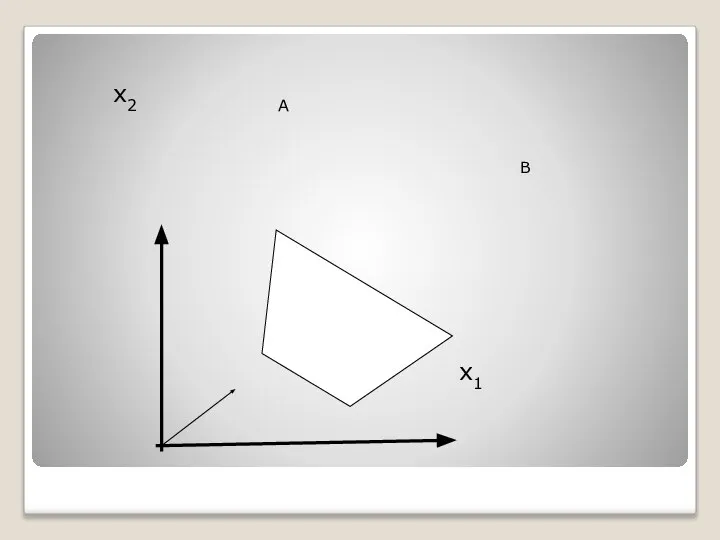
- 22. Из рис. 2 видно, что максимальное значение целевая функция принимает в любой точке отрезка АВ. На
- 23. х2 А В х1
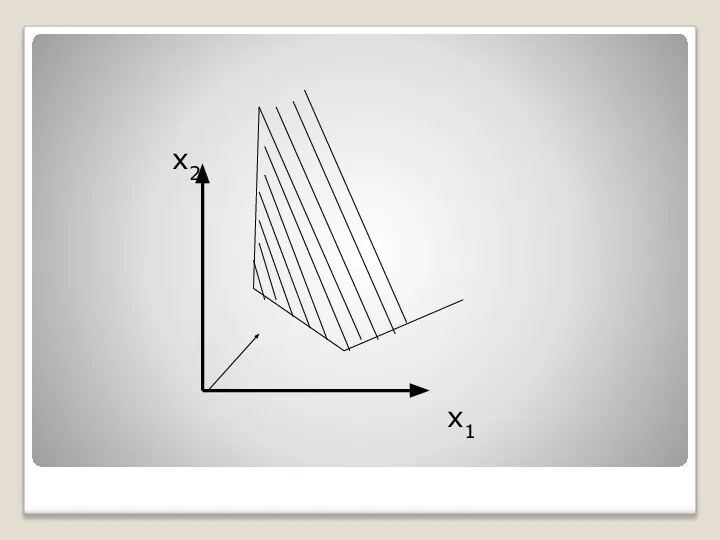
- 24. х2 х1
- 25. х2 х1
- 26. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при
- 27. Итак, нахождение решения задачи линейного программирования на основе ее геометрической интерпретации включает следующие этапы:
- 28. 1. Строят прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных
- 29. 2. Находят полуплоскости, определяемые каждым из ограничений задачи. 3. Находят многоугольник решений.
- 30. 4. Строят вектор целевой функции d(c1;c2),. 5. Строят прямую c1x1+ c2x2=h, проходящую через многоугольник решений.
- 31. 6. Передвигают прямую в направлении вектора , в результате чего - или находят точку (точки), в
- 32. 7. Определяют координаты точки максимума (минимума) функции и вычисляют значение целевой функции в этой точке.
- 33. Для изготовления двух видов продукции Р1 и Р2 используют 4 вида ресурсов S1 , S2 ,
- 35. Прибыль, полученная от единицы продукции Р1 и Р2 , - соответственно 2 и 3 руб. Необходимо
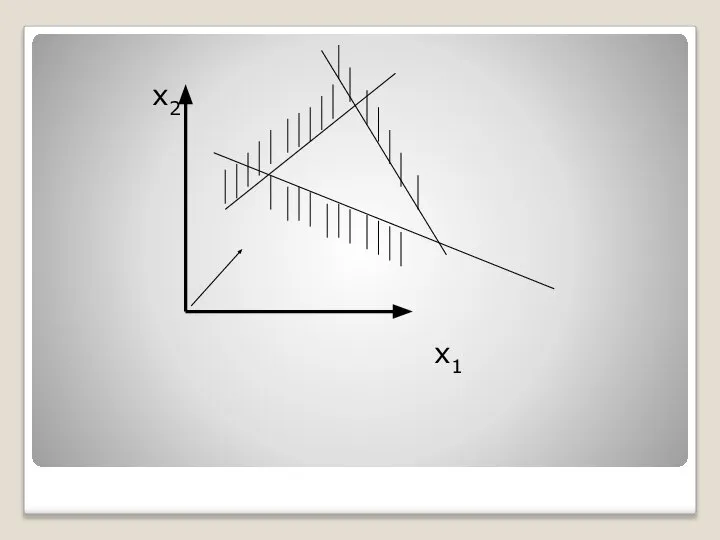
- 38. Найдем решение сформулированной задачи, используя ее геометрическую интерпретацию. Сначала построим многоугольник решений (область допустимых решений)
- 39. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных
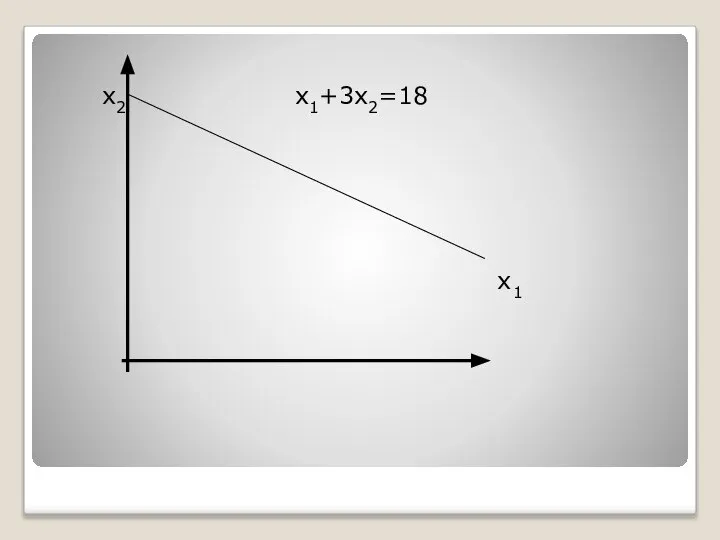
- 41. Х1+3х2=18
- 42. х2 х1+3х2=18 х1
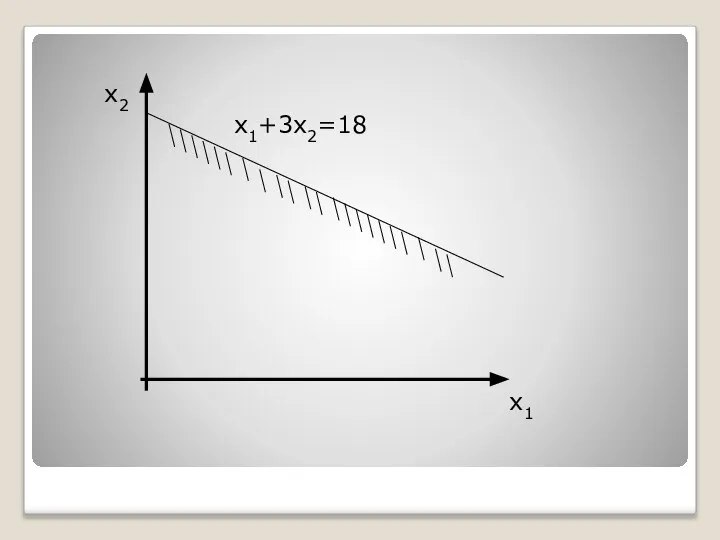
- 43. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли
- 44. х2 х1+3х2=18 х1
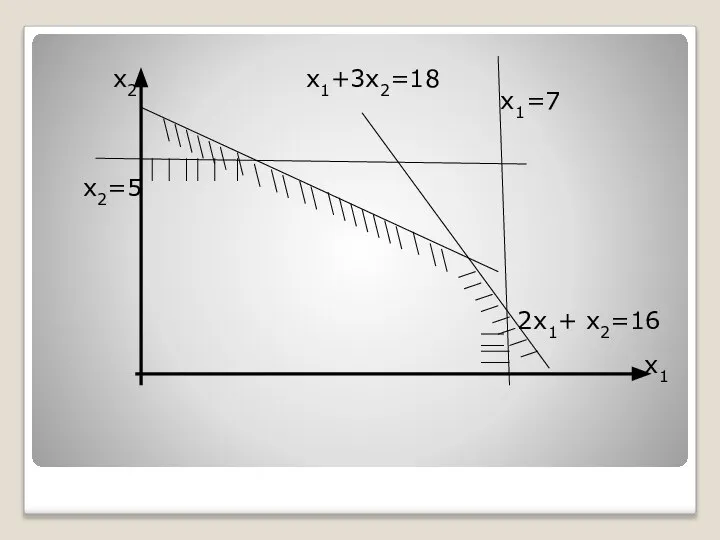
- 45. В результате получим:
- 46. х2 х1+3х2=18 х1=7 х2=5 2х1+ х2=16 х1
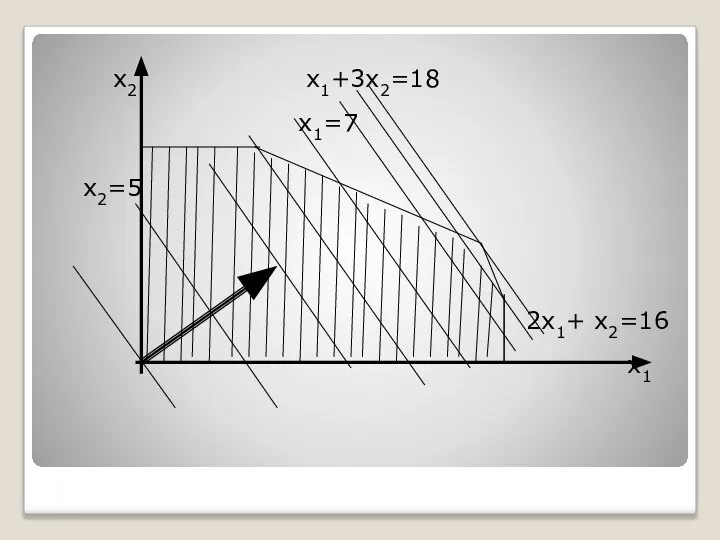
- 47. х2 х1+3х2=18 х1=7 х2=5 2х1+ х2=16 х1
- 48. х1+3х2=18 2х1+х2=16 х1=18-3х2 2(18-3х2)+х2=16 -5х2=-20 х2=4 х1= 6 F=2*6+3*4=24
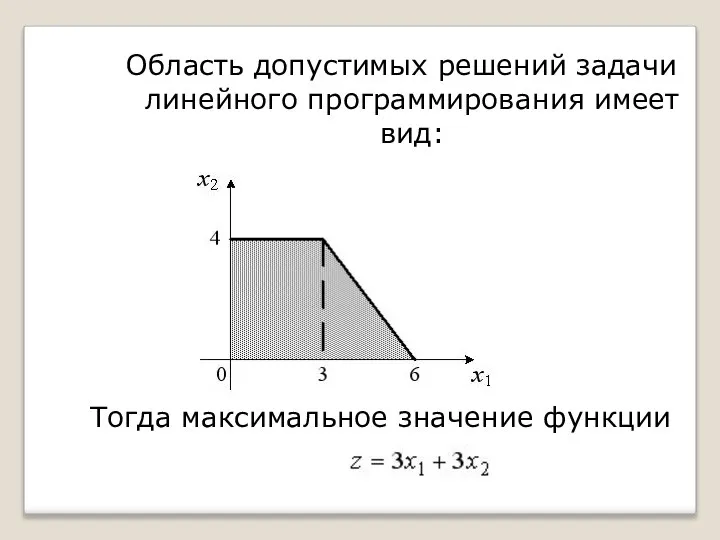
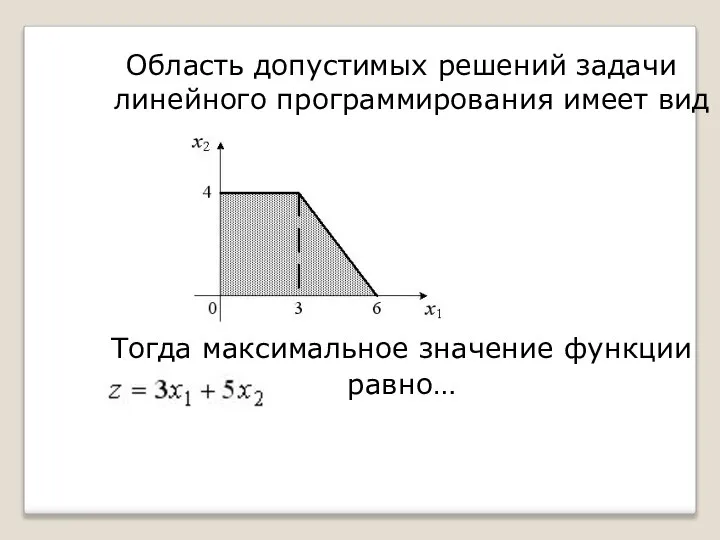
- 49. Область допустимых решений задачи линейного программирования имеет вид: Тогда максимальное значение функции равно…
- 50. Область допустимых решений задачи линейного программирования имеет вид Тогда максимальное значение функции равно…
- 51. Максимальное значение целевой функции при ограничениях равно…
- 52. Максимальное значение целевой функции при ограничениях равно…
- 54. Скачать презентацию





























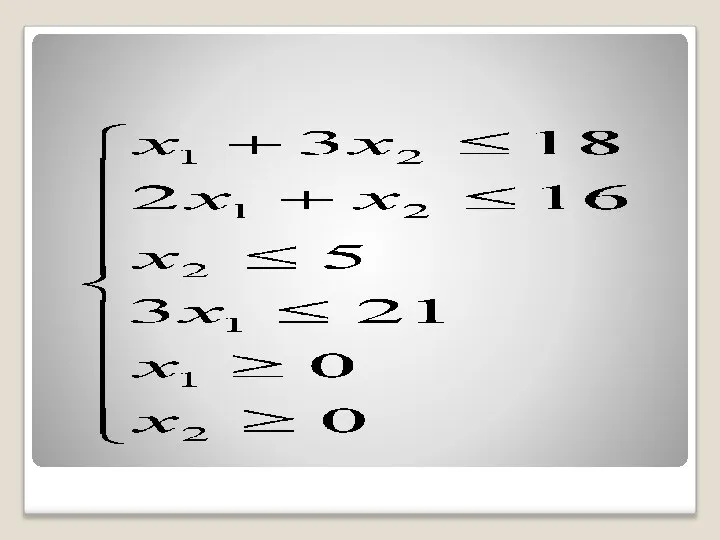
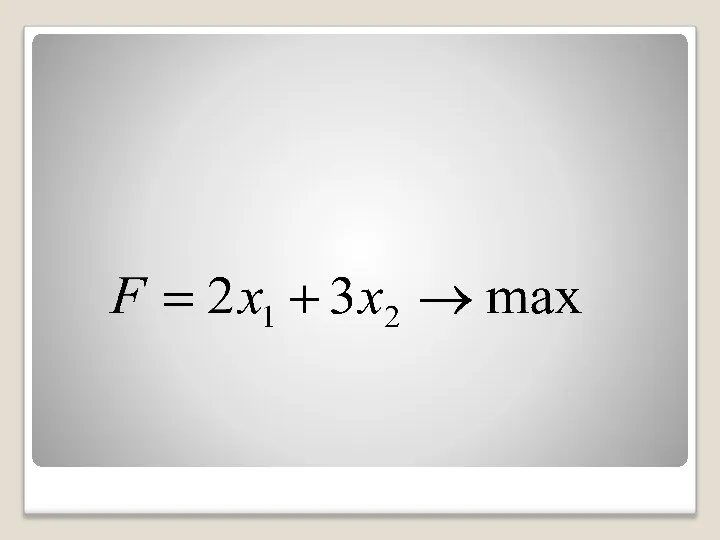


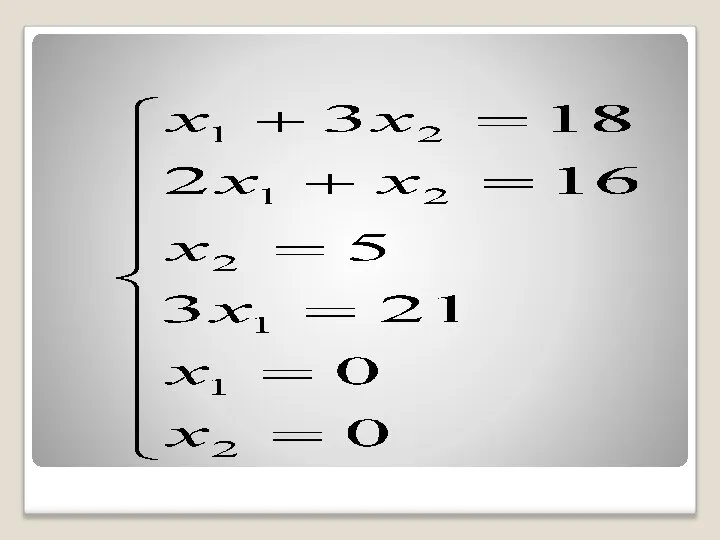



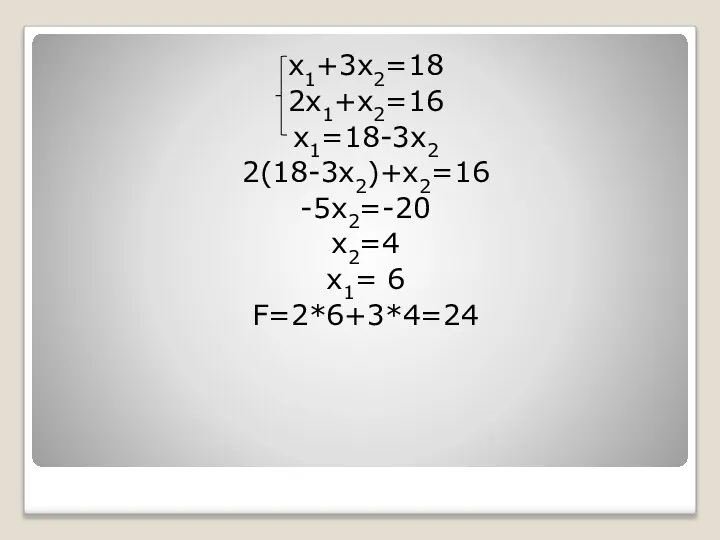


 Дидактический материал по ФЭМП. Занимательная математика
Дидактический материал по ФЭМП. Занимательная математика Первый Трест КП
Первый Трест КП Основы дисперсионного анализа. Однофакторный дисперсионный анализ
Основы дисперсионного анализа. Однофакторный дисперсионный анализ Построение сечения
Построение сечения Второй замечательный предел
Второй замечательный предел Решение задач на построение. Трудность использования настоящего циркуля при изображении окружностей на доске
Решение задач на построение. Трудность использования настоящего циркуля при изображении окружностей на доске Ряд Маклорена. (Тема 14.3)
Ряд Маклорена. (Тема 14.3) Пределы и непрерывность
Пределы и непрерывность Решение систем линейных неравенств с двумя переменными
Решение систем линейных неравенств с двумя переменными Связные графы. Компоненты связности. Понятие связности
Связные графы. Компоненты связности. Понятие связности Урок по математике 2 класс Приемы письменного вычитания вида 50-24 Выполнила: учитель начальных классов Пащенко У. А.
Урок по математике 2 класс Приемы письменного вычитания вида 50-24 Выполнила: учитель начальных классов Пащенко У. А. Основные понятия и аксиомы стереометрии
Основные понятия и аксиомы стереометрии Признаки равенства треугольников
Признаки равенства треугольников Змістовий модуль 2. Математична статистика
Змістовий модуль 2. Математична статистика Окружность. Длина окружности. Круг. Площадь окружности
Окружность. Длина окружности. Круг. Площадь окружности Презентация по математике "Арифметическая прогрессия в древности" -
Презентация по математике "Арифметическая прогрессия в древности" -  Решение нестандартных задач в рамках итогового повторения курса алгебры и начала анализа
Решение нестандартных задач в рамках итогового повторения курса алгебры и начала анализа Sie hat Geburtstag am fünften August. Er kommt am einunddreißigsten Juli
Sie hat Geburtstag am fünften August. Er kommt am einunddreißigsten Juli Кванторы. Квантор общности
Кванторы. Квантор общности Бенефис одной задачи «Пчелиный рой» Галкина Анастасия МОУ «СОШ с.Натальин Яр Перелюбского муниципального района Саратовск
Бенефис одной задачи «Пчелиный рой» Галкина Анастасия МОУ «СОШ с.Натальин Яр Перелюбского муниципального района Саратовск Тригонометрические формулы
Тригонометрические формулы Равенство треугольников
Равенство треугольников Кызыклы математика
Кызыклы математика Открытый банк заданий ЕГЭ по математике
Открытый банк заданий ЕГЭ по математике Осевая симметрия. 6 класс
Осевая симметрия. 6 класс Примеры на сложение от 0 до 9 (шпаргалка для первоклассника)
Примеры на сложение от 0 до 9 (шпаргалка для первоклассника) Первообразная в заданиях ЕГЭ (11 класс)
Первообразная в заданиях ЕГЭ (11 класс) Математика и Естественные Науки
Математика и Естественные Науки