Содержание
- 2. Производные высших порядков Итак: Производной n – ого порядка (или n – ой производной) называется производная
- 3. Производные высших порядков - производная пятого порядка. Начиная от производной 4 порядка , производные обозначаются римскими
- 4. Производные от функций, заданных параметрически Производная первого порядка от этой функции находится по формуле: Пусть функция
- 5. Производные от функций, заданных параметрически Вычислить производную 3 – ого порядка от функции:
- 6. Дифференциал функции Пусть функция y = f(x) имеет в некоторой точке х отличную от нуля производную,
- 7. Дифференциал функции Дифференциалом функции y = f(x) в точке х называется главная часть ее приращения: Дифференциал
- 8. Геометрический смысл дифференциала Проведем к графику функции y = f(x) в точке М(x, y) касательную х
- 9. Приложение дифференциала в приближенных вычислениях Как известно, приращение функции можно представить в виде: Это равенство позволяет
- 11. Скачать презентацию








 Исследование лабиринтов
Исследование лабиринтов Свойство дроби. Сравнение обыкновенных дробей
Свойство дроби. Сравнение обыкновенных дробей Рациональные числа
Рациональные числа Свойства коэффициентов множественной регрессии
Свойства коэффициентов множественной регрессии ЕГЭ профильная математика. Задание № 4
ЕГЭ профильная математика. Задание № 4 Основные темы курса: Теория множеств, теория вероятности, элементы комбинаторики, элементы статистики
Основные темы курса: Теория множеств, теория вероятности, элементы комбинаторики, элементы статистики Сфера и шар
Сфера и шар Определители матриц. Обратная матрица, ранг матрицы
Определители матриц. Обратная матрица, ранг матрицы Цель диагностики математического развития детей
Цель диагностики математического развития детей Презентация по математике "Умножение и деление чисел на 10, 100" - скачать
Презентация по математике "Умножение и деление чисел на 10, 100" - скачать  Презентация по математике "Интегралы" - скачать
Презентация по математике "Интегралы" - скачать  МНР-машины. Программа машины
МНР-машины. Программа машины Сети Петри
Сети Петри Основы оптимизации перевозочного процесса. Маршрутизация перевозок массовых грузов
Основы оптимизации перевозочного процесса. Маршрутизация перевозок массовых грузов Сравнение десятичных дробей
Сравнение десятичных дробей Нахождение значений дробных выражений. 6 класс
Нахождение значений дробных выражений. 6 класс Матрицы и действия над ними
Матрицы и действия над ними Структура курсовой работы по дисциплине «Элементарная математика»
Структура курсовой работы по дисциплине «Элементарная математика» Система MatLab. Методические указания к выполнению лабораторных работ
Система MatLab. Методические указания к выполнению лабораторных работ Краткие сведения об аппроксимации функций
Краткие сведения об аппроксимации функций Точечное оценивание параметров распределений случайных величин
Точечное оценивание параметров распределений случайных величин Способы решения одной задачи. Мастер-класс
Способы решения одной задачи. Мастер-класс Функции y = ax^2 + n и y = a(x – m)^2
Функции y = ax^2 + n и y = a(x – m)^2 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Задача Коши.
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Задача Коши. Линейное программирование
Линейное программирование Понятие системы уравнений с двумя переменными
Понятие системы уравнений с двумя переменными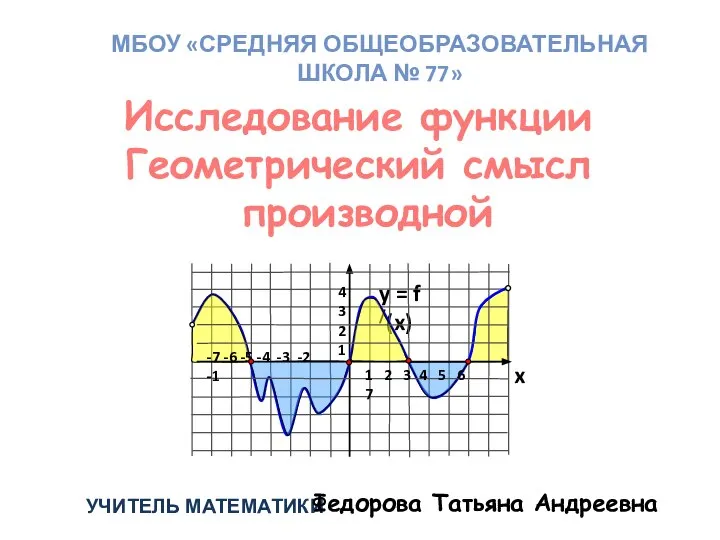 Исследование функции. Геометрический смысл производной
Исследование функции. Геометрический смысл производной Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости. МОУ СОШ №256 г.Фокино. 2007 г.
Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости. МОУ СОШ №256 г.Фокино. 2007 г.