МНР-машины. Программа машины

Август 23, 2022

Главная
Математика
МНР-машины. Программа машины

Содержание

2. Впервые МНР была рассмотрена Шепердсоном и Стерджисом в 1963 году. Машина с неограниченными регистрами (МНР) -
3. 2) Программа машины - это конечная последовательность I1, I2, . . . , Is из следующих
4. Вычисление функций на машинах с неограниченными регистрами. Как и в случае машин Тьюринга, необходимо указать, как
5. Пример. Пусть задана программа Р следующего вида: I1 J(1, 2, 6) I2 S(2) I3 S(3) I4
6. Для данного примера МНР остановится, когда содержимое регистров R1 и R2 будут одинаковы (через 2 цикла)
7. МНР-вычислимые функции Через Р(a1,a2, . . . an) обозначим вычисление по программе Р с начальной конфигурацией
9. 3. f(x) = 1/2x, если x – четно, не определено, если x – нечетно. Если x
10. Разрешимые предикаты. Определение разрешимости предикатов в точности совпадает с ранее данным определением (см. частично рекурсивные функции).
11. Вычислимость на других областях Поскольку МНР работает только с натуральными числами, наше определение вычислимости и разрешимости
12. Пример. Рассмотрим область Z. Явное кодирование можно задать функцией а, где a(n) = 2n, если n≥0,
14. Стандартный вид программы. Сложная программа часто содержит другие программы в качестве строительных блоков - подпрограмм. Для
15. Определение .Стандартизацией программы I1 , I2 , … ,Is называется замена в данной программе всех команд
16. Выделения регистров для подпрограммы. Пусть программа P используется как подпрограмма в основной программе Q. В некоторых
17. Правило выделения регистров Пусть ρ = ρ(P) количество регистров, затрагиваемых программой P, и программа P меняет
18. Вставка подпрограммы. Пусть в программе Q имеется подпрограмма P для вычисления функции f (x1,x2,...,xn). В подпрограмме
19. Для осуществления такой пересылки аргументов выполняется следующее действие. 1) Перед командами из P размещается набор команд
20. Для правильной работы подпрограммы P могут потребоваться следующие действия, которые назовем вставкой подпрограммы. Вставка подпрограммы P
21. В итоге в основной программе получается следующий фрагмент T(i1, 1) . . . T(in, n) Z(n
22. Вычислимость частично рекурсивных функций на МНР. Если функция f вычислима на некоторой машине с неограниченными регистрами,
23. Оператор суперпозиции. Теорема 1. Пусть функция f получена из функций h, g1, g2, … , gm
24. Процесс вычисления функции f(x1, x2, . . . , xn) состоит в следующем. Последовательно вычисляем числа
25. В программе вставлены несколько подпрограмм. Модифицируем правило вставки для случая нескольких подпрограмм. 1) Вычисляем число ρ
26. 2) Командами T(1, ρ + 1), . . . , T (n, ρ + n) пересылаем
27. Оператор примитивной рекурсии. Теорема 2. Пусть функция f получена с помощью операторапримитивной рекурсии из функций g
28. Программа для реализации оператора примитивной рекурсии имеет вид. T(1, ρ + 1) . . . T(n
29. Комментарии к работе программы: 1) Вычисляем число ρ = max (n + 2, ρ(G), ρ(H)). Обозначим
30. Таким образом, перед первым выполнением команды Iq имеем следующее содержание регистров. • В регистре Rt+1 число
31. При этом числа x1, x2, . . . , xn извлекаются из хранилища Rρ+1, . .
32. Оператор минимизации. Алгоритм вычислений. Теорема 3. Пусть функция f получена из функции g с помощью оператора
33. Программа для вычисления функции f(x1, x2, . . . , xn) имеет вид. T(1, ρ +
34. Комментарии к работе программы: Рассмотрим число ρ = max(n+1, ρ(G)), и произведем следующее распределение памяти МНР.
36. Скачать презентацию

Слайд 2

Впервые МНР была рассмотрена Шепердсоном и Стерджисом в 1963

году.
Машина с неограниченными регистрами (МНР) - это абстрактная машина, более сходная с реальным компьютером по сравнению с машиной Тьюринга. Она имеет следующие составные части.
1) Регистры R1,R2,R3, . . ., в которых содержатся соответственно
натуральные числа r1, r2, r3, . . .
R1 R2 R3 . . . Rk Rk+1 . . .
Число регистров бесконечно, но только конечное множество регистров содержит числа, отличные от нуля. Все остальные регистры Rk+1,Rk+2R1,R2, . . . , Rk , . . . заполнены нулями.

Слайд 3

2) Программа машины - это конечная последовательность
I1, I2, . .

. , Is из следующих четырех типов команд:
• Команда обнуления Z(n) делает содержимое регистра Rn равным нулю.
• Команда прибавления единицы S(n) к содержимому регистра Rn
прибавляет число 1.
• Команда переадресации T(m, n) заменяет содержимое регистра
Rn на содержимое регистра Rm.
• Команда условного перехода J(m, n, q) сравнивает содержимое
регистров Rm и Rn. При rm = rn в качестве следующей команды
выполняется команда с номером q. Если rn ≠ rm, то выполняется
следующая по порядку команда программы.
Команды обнуления, прибавления единицы и переадресации называются арифметическими командами.

Слайд 4

Вычисление функций на машинах с неограниченными регистрами.
Как и в

случае машин Тьюринга, необходимо указать, как машина с неограниченными регистрами вычисляет частичную функцию f(x1,x2, ... , xn) от n аргументов.
Рассмотрим набор аргументов (x1,x2, ... , xn) и разместим число x1 в регистре R1 , число x2 – в регистре R2, ..., число xn - в регистре Rn. Все остальные регистры заполнены нулями. Получаем начальную конфигурацию МНР.
После окончания работы в регистре R1 должно быть значение функции f(x1,x2, ... ,xn) . Если значение f(x1,x2, ... , xn) не определено, то МНР должна работать бесконечно.

Слайд 5

Пример. Пусть задана программа Р следующего вида:
I1 J(1, 2, 6)
I2

S(2)
I3 S(3)
I4 J(1, 2, 6)
I5 J(1, 1, 2)
I6 T(3,1)
и начальная конфигурация
R1 R2 R3 . . . Rk Rk+1 . . .
Пусть , в общем случае, программа имеет вид: I1 I2 … Is.
1) МНР всегда начинает работу с команды I1.
2) МНР останавливается тогда и только тогда, когда нет следующей команды, т.е. следующей командой должна выполняться команда Ir, где r > s. Это может произойти в одном из следующих случаев:
- если выполнена к-да Is и Is - арифметическая к-да;
- если выполнена к-да Ik = J(m, n, q), rm= rn и q > s;
- если выполнена к-да Ik = J(m, n, q), rm≠ rn и k = s, т.е. выполнена последняя к-да в программе, за которой д.б. переход на следующую к-ду, которой нет.

Слайд 6

Для данного примера МНР остановится, когда содержимое регистров R1 и

R2 будут одинаковы (через 2 цикла) и к-да I6 перешлет содержимое регистра R3 (который увеличивается на 1 при каждом прохождении циклического участка и станет равным 2 после 2-х циклов) в регистр R1. Программа остановится, т.к. в ней нет к-ды I7.
Отметим, что в нашей программе к-да I5 = J(1, 1, 2) является, по-существу, безусловным переходом на к-ду I2 , т.к. r1= r1 всегда.
Вычисление по нашей программе с заданной начальной конфигурацией останавливается в заключительном состоянии:
При написании программ для МНР часто полезным оказывается предварительное составление диаграммы переходов (блок-схемы), построение программы по которой оказывается лишь кодированием на язык МНР.

Слайд 7

МНР-вычислимые функции
Через Р(a1,a2, . . . an) обозначим вычисление

по программе Р с начальной конфигурацией a1,a2, . . . an. Содержимое остальных регистров равно 0.
Записью Р(a1,a2, . . . an)↓ будем обозначать завершимость выполнения программы, т.е.тот факт что вычисление в конце концов остановится.
Пусть f частичная функция из Nn в N, т.е. f:Nn → N, P – программа, и a1,a2, . . . an , b ∈ N.
Определение. Вычисление Р(a1,a2, . . . an) сходится к b, если Р(a1,a2, . . . an)↓ и в заключительной конфигурации в регистре R1 находится b. Этот факт записывается как Р(a1,a2, . . . an)↓ b.
Определение. Программа Р МНР-вычисляет функцию f, если для всех a1,a2, . . . an , b имеет место Р(a1,a2, . . . an)↓ b тогда и только тогда, когда (a1,a2, . . . an) ∈ Dom(f) и f (a1,a2, . . . an) = b.
Определение. Функция f называется МНР-вычислимой, если существует программа, которая МНР-вычисляет f.

Слайд 8

Слайд 9

3. f(x) = 1/2x, если x – четно,
не определено, если

x – нечетно.
Если x – нечетно, то программа не останавливается.
Алгоритм вычисления: Изменяем содержимое двух регистров, в одном из которых находится число k, а в другом 2k, где k пробегает ряд значений 0,1,2,3,… .Для последовательных значений проверяется, верно ли, что x = 2k. Если да, то ответ k, иначе увеличить k на единицу и повторить предыдущую команду. Если x нечетно, то эта процедура никогда не остановится.
Начальная конфигурция: x,0,0,0,…..
Типичная конфигурция: x,2k,k,0,…..
МНР-программа Р:
I1 J(1, 2, 6)
I2 S(3)
I3 S(2)
I4 S(2)
I5 J(1, 1, 1)
I6 T(3,1)
Таким образом, функция f(x) является МНР-вычислимой.

Слайд 10

Разрешимые предикаты.
Определение разрешимости предикатов в точности совпадает с ранее данным

определением (см. частично рекурсивные функции).
Примеры.
Предикат “x = 0” разрешим. Его характеристическая функция вычисляется следующей программой:
I1 J(1, 2, 3)
I2 J(1, 1, 4)
I3 S(2)
I4 Т(2, 1)
Док-во разрешимости предикатов “x ≠ y”, “x кратно y” и др. – в упражнениях.

Слайд 11

Вычислимость на других областях
Поскольку МНР работает только с натуральными

числами, наше определение вычислимости и разрешимости применимо только к функциям и предикатам от натуральных чисел. Эти понятия легко распространяются на другие виды объектов (т. е. целые числа, полиномы, матрицы и т. д.) с помощью кодирования.
Кодированием области D объектов называется явное и эффективное отображение a:D→ N.
Мы будем говорить, что объект d∈D кодируется натуральным числом a(d).
Предположим, что f является функцией из D в D; тогда f естественно кодируется функцией f* из N в N, которая отображает код каждого объекта d ∈ Dom (f) в код объекта f (d).
В явном виде это можно записать как f* = a∙f∙a-1.
Таким рбразом, можно распространить определение МНР-вычислимости на область D, полагая функцию f вычислимой, если f* - вычислимая функция натуральных чисел.

Слайд 12

Пример. Рассмотрим область Z. Явное кодирование можно задать функцией а, где

a(n) = 2n, если n≥0,
-2п -1, если n < 0.
Тогда a-1 задается так:
a-1(m) = 1/2m, если m четно,
-1/2 (m+1), если m нечетно.
Теперь рассмотрим функцию f(x) = х - 1 на Z. Построим f*:N→N, задаваемую как:
f*(x) = 1, если х = 0 (т. е. х=а(0)),
х- 2, если x > 0 и х четно (т. е. х = а(п), n>0),
х + 2, если х нечетно (т. е. x = а(n), n < 0).
Написание программы, которая вычисляет f•, является рутинным упражнением. Таким образом, х-1 есть вычислимая функция на Z.
Приведенное выше определение очевидным образом pacширяется на n-местные вычислимые функции на области D и на разрешимые предикаты на области D.

Слайд 13

Слайд 14

Стандартный вид программы.
Сложная программа часто содержит другие программы в

качестве строительных блоков - подпрограмм. Для правильного взаимодействия этих подпрограмм нужно соблюдать некоторые правила.
Определение. Пусть дана программа для МНР, состоящая из s команд. Будем говорить, что программа имеет стандартный вид, если во всякой команде условного перехода J(m,n,q) данной программы выполняется неравенство q < s + 1. Если программа P не имеет стандартного вида, то в ней найдется команда вида J(m, n, q), где q > s+1. Заменим в программе P эту команду на команду J(m,n, s + 1).
Получим программу P', выполняющую точно такое же действие, как и программа P. Действительно, P и P' отличаются лишь командами J(m, n, q) и J(m,n, s + 1). Однако действие этих команд одинаково: при rm≠ rn нужно перейти к следующей по порядку команде, а при rm = rn остановиться.

Слайд 15

Определение .Стандартизацией программы I1 , I2 , … ,Is называется замена

в данной программе всех команд J(m, n, q) где q > s+1, на команды J(m, n, s + 1).
В результате стандартизации из программы P нестандартного вида получим стандартную программу P' с тем же действием. Используя P' вместо P, считаем, что все программы, которые мы рассматриваем, стандартны.
Соединение программ.
Определение. Соединением программ P: I1, I2..., Is и Q: I’1, I’2, ..., I’t называется программа из s+t команд вида I1, I2, ..., Is, Is+1, Is+2 , ..., Is+t, где команды Is+1, Is+2 , ..., Is+t получены из команд I’1, I’2, ..., I’t программы Q приращением номеров на число s. При этом каждая команда условного перехода J(m, n, q) из Q заменена на команду вида J(m, n, q+s ).
Соединение программ P и Q будем обозначать через PQ. Можно соединить программы P, Q, R и получить программу PQR=(PQ)R и т.д.

Слайд 16

Выделения регистров для подпрограммы.
Пусть программа P используется как

подпрограмма в основной программе Q. В некоторых регистрах хранятся данные основной программы. При выполнении подпрограммы P можно испортить данные основной программы Q.
Для предотвращения такой потери данных делаем так, что основная
программа изменяет одну область регистров, а подпрограмма—другую.
Произвольная МНР-программа P имеет конечное число команд. Команда обнуления Z(n) и команда прибавления единицы S(n) действуют только на один регистр Rn.
Команде переадресации T(m, n) и команде условного перехода J(m,n,q) для функционирования нужны два регистра Rm и Rn.
Если общее число команд обнуления и прибавления единицы равно k, а число команд переадресации и условного перехода равно m, то для ра боты всей программы P достаточно зарезервировать k+2m регистров.
На остальные регистры программа P не действует, и их можно использовать в качестве рабочих регистров основной программы. Поэтому в дальнейшем применяем следующее правило выделения регистров подпрограммы P в программе Q.

Слайд 17

Правило выделения регистров
Пусть ρ = ρ(P) количество регистров, затрагиваемых

программой P, и программа P меняет лишь регистры R1, . . . , Rρ и не затрагивает регистры Rk для k > ρ. Отводим регистры R1, . . . , Rρ для работы подпрограммы P, и выделяем регистры Rk при k > ρ в качестве рабочих регистров для остальных команд основной программы Q.
Это правило изображено в следующем виде
R1, . . . , Rρ, Rρ+1, . . .
Если соблюдено правило выделения регистров, то программа P в процессе выполнения меняет лишь регистры R1, . . . , Rρ, а данные программы Q находятся в регистрах Rρ+1, . . . и не могут быть затронуты и испорчены программой P.

Слайд 18

Вставка подпрограммы.
Пусть в программе Q имеется подпрограмма P для

вычисления функции f (x1,x2,...,xn). В подпрограмме P имеются входные данные x1,x2,...,xn и результат вычислений f (x1,x2,...,xn).
По определению МНР должны соблюдаться следующие требования.
При старте P аргументы (x1,x2,...,xn) обязаны находиться в регистрах R1, ... ,Rn..
2. После окончания работы подпрограммы P результат f (x1,x2,...,xn) должен содержаться в регистре R1.
Однако в ходе работы основной программы Q возможен переход к выполнению подпрограммы P, которой нужны аргументы x1, x2, ..., xn. В данный момент аргументы хранятся в каких-то регистрах Ri1, ... , Rin , а не в регистрах R1, ... , Rn , как нужно.

Слайд 19

Для осуществления такой пересылки аргументов выполняется следующее действие.
1) Перед командами

из P размещается набор команд
T(i1, 1), . . . , T (in, n).
Пусть основная программа Q вызвала подпрограмму P и в начало
зарезервированных регистров R1, . . . , Rρ скопированы числа x1, . . . , xn, с которыми начнет работать подпрограмма P. Однако в регистрах
Rn+1, . . . , Rρ может оставаться мусор - произвольные числа, оставшиеся от предыдущей работы Q. По правилам работы МНР в последующих
регистрах Rn+1, . . . , Rk должны быть только одни нули. Поэтому нужно
выполнить обнуление этих регистров от мусора, которое осуществляется следующим способом.
2) Выполняется набор команд Z(n+1), . . . , Z(ρ).
После выполнения подпрограммы P результат находится в регистре
R1. Однако регистр R1 нужен для последующих вычислений программы Q.
Поэтому из регистра R1 результат выполнения подпрограммы P нужно пересылать для его последующего использования на хранение в некоторый рабочий регистр Ri, где i >ρ(P). Это можно осуществить следующим способом.
3) Выполняется команда переадресации T(1, i).

Слайд 20

Для правильной работы подпрограммы P могут потребоваться
следующие действия, которые назовем

вставкой подпрограммы.
Вставка подпрограммы P в основную программу МНР - это выполнение следующих действий 1–5.
1. Распределение памяти. Вычисляется число ρ = ρ(P) и выделяется
память R1, . . . , Rρ, достаточная для работы подпрограммы P. Задается
регистр Ri, где i > ρ, для хранения результата работы подпрограммы.
2. Извлечение аргументов. Для этого записываются следующие команды:
T(i1, 1), . . . , T (in, n)
для передачи аргументов из места их хранения в регистры R1, . . . , Rn.
3. Очистка регистров. Для этого записываются следующие команды:
Z(n + 1), . . . , Z(ρ).
4. Вставка команд подпрограммы P.
5. Пересылка результата на хранение. Добавляется команда T(1, i).

Слайд 21

В итоге в основной программе получается следующий фрагмент
T(i1, 1)
. .

.
T(in, n)
Z(n +1)
. . .
Z(ρ)
P
T(1, i)

Вставку данного фрагмента в основную программу обозначаем через P[i1, . . . , in → i ]

Слайд 22

Вычислимость частично рекурсивных функций на МНР.
Если функция f вычислима

на некоторой машине с неограниченными регистрами, то говорим кратко «Функция f МНР-вычислима». В предыдущей части установлена МНР-вычислимость простейших функций.
Покажем, что применение операторов суперпозиции, примитивной рекурсии и минимизации к МНР вычислимым функциям вырабатывает МНР- вычислимые функции.
В результате получим основной результат - все частично рекурсивные функции вычислимы на МНР.

Слайд 23

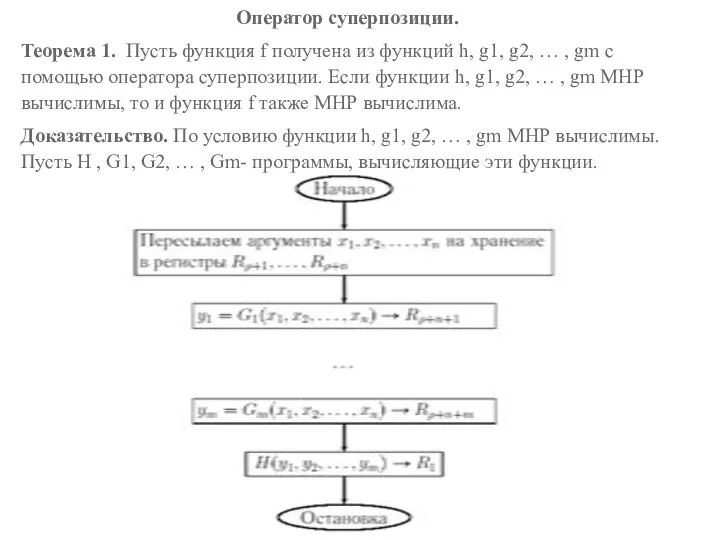
Оператор суперпозиции.
Теорема 1. Пусть функция f получена из функций h,

g1, g2, … , gm с помощью оператора суперпозиции. Если функции h, g1, g2, … , gm МНР вычислимы, то и функция f также МНР вычислима.
Доказательство. По условию функции h, g1, g2, … , gm МНР вычислимы. Пусть H , G1, G2, … , Gm- программы, вычисляющие эти функции.

Слайд 24

Процесс вычисления функции f(x1, x2, . . . , xn)

состоит в следующем.
Последовательно вычисляем числа
y1 = g1(x1, x2, . . . , xn),
y2 = g2(x1, x2, . . . , xn),
. . .
ym = gm(x1, x2, . . . , xn)
с помощью соответствующих программ G1,G2, . . . , Gm. Затем вычисляем
число h(y1, . . . , ym) с помощью программы H. Получаем f(x1, x2, . . . , xn).

Программа для реализации оператора суперпозиции имеет вид.
T(1, ρ +1)
. . .
T(n, ρ +n)
G1[ρ + 1, ρ + 2, . . . , ρ + n → ρ + n + 1]
. . .
Gm[ρ +1, ρ + 2, . . . , ρ +n → ρ + n + m]
H[ρ + n + 1, . . . , ρ + n + m → 1]

Слайд 25

В программе вставлены несколько подпрограмм.
Модифицируем правило вставки для

случая нескольких подпрограмм.
1) Вычисляем число ρ = max(n, m, ρ(G1), . . . , ρ(Gm), ρ(H)), и производим следующее распределение памяти МНР.
• Регистры R1, . . . , Rρ предназначены для работы всех подпрограмм G1,G2, . . . , Gm,H.
• Последующие регистры Rρ+1, . . . , Rρ+n выделены в качестве постоянного хранилища аргументов x1, x2, . . . , xn.
• Следующие по порядку регистры Rρ+n+1, . . . , Rρ+n+m являются рабочими регистрами основной программы, в которых сохраняются результаты работы подпрограмм G1,G2, . . . , Gm, соответственно.
Эти аргументы затем вычисляет f(x1, x2, . . . , xn) и пересылает результат в регистр R1.

Слайд 26

2) Командами T(1, ρ + 1), . . . , T

(n, ρ + n) пересылаем аргументы x1, x2, . . . , xn на место их постоянного хранения—регистры Rρ+1, . . . , Rρ+n. Из этих регистров в процессе работы подпрограмм несколько раз будут считываться аргументы x1, x2, . . . , xn и пересылаться в регистры R1, . . . , Rn. Именно из этих регистров подпрограммы G1,G2, . . . , Gm будут извлекать свои аргументы при старте.
3) Подпрограммы Gi, где i = 1, . . . , m, вставляются в основную программу по правилу вставки подпрограмм. Далее вставляется подпрограмма H для вычисления функции h. Аргументы функции h равны y1 = g1(x1, . . . , xn). . . , ym = gm(x1, . . . , xn) и хранятся в регистрах Rρ+n+1, . . . , Rρ+n+m. Подпрограмма H считывает эти аргументы, затем вычисляет f(x1, x2, . . . , xn) и пересылает результат в регистр R1. Затем МНР останавливается.
Теорема доказана.

Слайд 27

Оператор примитивной рекурсии.
Теорема 2. Пусть функция f получена с помощью

операторапримитивной рекурсии из функций g и h. Если функции g и h МНР-вычислимы, то и функция f также МНР-вычислима.
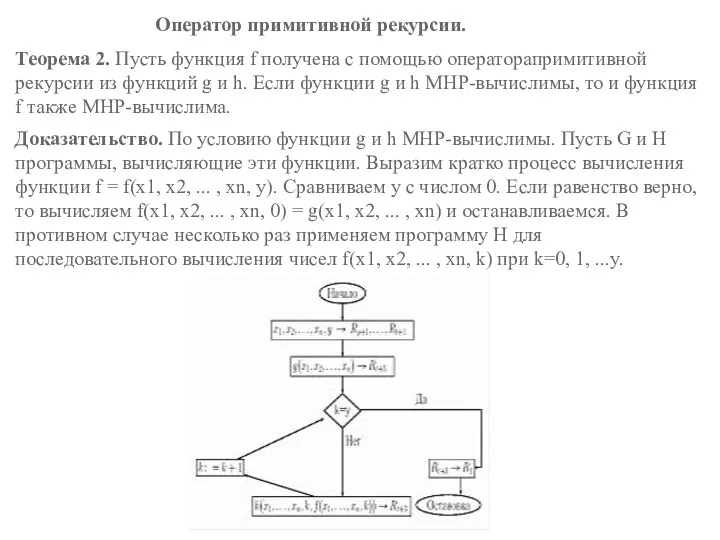
Доказательство. По условию функции g и h МНР-вычислимы. Пусть G и H программы, вычисляющие эти функции. Выразим кратко процесс вычисления функции f = f(x1, x2, ... , xn, y). Сравниваем y с числом 0. Если равенство верно, то вычисляем f(x1, x2, ... , xn, 0) = g(x1, x2, ... , xn) и останавливаемся. В противном случае несколько раз применяем программу H для последовательного вычисления чисел f(x1, x2, ... , xn, k) при k=0, 1, ...y.

Слайд 28

Программа для реализации оператора примитивной рекурсии имеет
вид.
T(1, ρ +

1)
. . .
T(n + 1, t + 1)
G[1, 2, . . . , n → t +3]
Iq J(t + 2, t + 1, p)
H[ρ + 1, . . . , ρ + n, t + 2, t + 3 → t +3] S(t + 2)
J(1, 1, q)
Ip T(t + 3, 1)
При этом Iq и Ip—просто особо отмеченные команды с некоторыми но-
мерами q и p.

Слайд 29

Комментарии к работе программы:
1) Вычисляем число ρ = max (n +

2, ρ(G), ρ(H)). Обозначим ρ + n = t.
Регистры для работы программы распределим следующим способом.
• R1, . . . , Rρ—регистры для подпрограмм G и H;
• Rρ+1, . . . , Rt+1—регистры, для постоянного хранилища аргументов
x1, x2, . . . , xn, y.
• Rt+2,Rt+3—два регистра для запоминания промежуточных значений k и f(x1, x2, . . . , xn, k) в цикле, где k = 0, 1, . . . , y. Перед первым исполнением цикла в регистрах Rt+2 и Rt+3 разместим 0 и
f(x1, x2, . . . , xn, 0).
2) Командами T(1, ρ + 1), . . . , T (n + 1, t + 1) пересылаем n + 1 аргументов x1, x2, . . . , xn, y на место их постоянного хранения—регистры
Rρ+1, . . . , Rt+1.
Затем в регистр Rt+3 помещаем число g(x1, x2, . . . , xn), равное
f(x1, x2, . . . , xn, 0). Это выражено вставкой в программу строки
G[1, 2, . . . , n → t +3].
Таким образом, перед первым выполнением команды Iq
имеем следующее содержание регистров.
• В регистре Rt+1 число y. Оно не будет изменяется в процессе выполнения цикла.

Слайд 30

Таким образом, перед первым выполнением команды Iq
имеем следующее содержание регистров.
•

В регистре Rt+1 число y. Оно не будет изменяется в процессе выполнения цикла.
• В регистре Rt+2 число k = 0. Оно будет наращиваться на 1 при каж-
дом проходе цикла.
• В регистре Rt+3 число f(x1, x2, . . . , xn, k) при k = 0. Число k будет
наращиваться на 1 при каждом проходе цикла.
3) Выполнение команды Iq начинает цикл. Возвращение на повторе-
ние этой команды производит команда J(1, 1, q). Сравниваются число
rt+2 = k и число rt+1, всегда равное y. Число rt+2 = k принимает значения
0, 1, . . . , y. Для его приращение на 1 предназначена команда S(t + 2).
Поэтому в цикле последовательно проверяются равенства
0 = y, 1 = y, . . . y = y.
Пусть равенство еще не выполнено. Тогда выполняется вставка
H[ρ +1, . . . , ρ + n, t + 2, t + 3 → t +3]. Она вычисляет функцию
h(x1, x2, . . . , xn, k, f(x1, x2, . . . , xn, k)),
т.е. число
f(x1, x2, . . . , xn, k + 1).

Слайд 31

При этом числа x1, x2, . . . , xn

извлекаются из хранилища
Rρ+1, . . . , Rρ+n, число k - из Rt+2, число f(x1, x2, . . . , xn, k) - из Rt+3. Новое число f(x1, x2, . . . , xn, k + 1) заменяет старое число f(x1, x2, . . . , xn, k) в регистре Rt+3. Поэтому при следующем исполнении цикла в Rt+2 будет число
k +1, в Rt+3—число f(x1, x2, . . . , xn, k + 1), что и нужно.
Равенство rt+2 и rt+1 в команде Iq сработает лишь тогда, когда в регистре Rt+2 накопится число y. В этот момент в регистре Rt+3 находится число f(x1, x2, . . . , xn, y). Выполнится переадресация к команде
T(t+3, 1),
которая перешлет f(x1, x2, . . . , xn, y) в регистр R1.После этого
МНР остановится.
Теорема доказана.

Слайд 32

Оператор минимизации. Алгоритм вычислений.
Теорема 3. Пусть функция f получена

из функции g с помощью оператора минимизации. Если функция g является МНР-вычислимой, то и функция f также МНР-вычислима.
Доказательство. Построим программу, вычисляющую функцию f. Пусть G – программа, вычисляющая функцию g. Будем считать, что программа G приведена к стандартному виду.
Искомая программа для функции f будет проверять одно за другим следующие равенства:
g(x1,x2,...,xn,0)=0,
g(x1,x2,...,xn,1)=0,
...........................
g(x1,x2,...,xn,y)=0,
g(x1,x2,...,xn,k)=0.
стремясь найти наименьшее k с условием g(x1, x2, . . . , xn, k) = 0.

Слайд 33

Программа для вычисления функции f(x1, x2, . . . , xn)

имеет вид.
T(1, ρ + 1)
. . .
T(n, ρ + n)
Ip G[ρ +1, ρ + 2, . . . , ρ + n + 1 → 1]
J(1, ρ +n + 2, q)
S(ρ + n + 1)
J(1, 1, p)
Iq T(ρ + n + 1, 1)
При этом Ip является первой командой подпрограммы
G[ρ +1, ρ + 2, . . . , ρ + n + 1 → 1].

Слайд 34

Комментарии к работе программы:
Рассмотрим число ρ = max(n+1, ρ(G)), и произведем

следующее распределение памяти МНР.
• Регистры R1, . . . , Rρ предназначены для работы подпрограммы G.
• Регистры Rρ+1, . . . , Rρ+n предназначены для постоянного хранения
аргументов x1, x2, . . . , xn.
• Последующий регистр Rρ+n+1 выделен для хранения числа k в проверяемых равенствах g(x1, x2, . . . , xn, k) = 0, где k = 0, 1, 2, . . . .
2) Командами T(1, ρ + 1), . . . , T (n, ρ + n) пересылаем аргументы
x1, x2, . . . , xn на место их постоянного хранения—регистры
Rρ+1, . . . , Rρ+n.
3) Затем работает подпрограмма G[ρ+1, ρ+2, . . . , ρ+n+1 → 1], которая начинает цикл. Он начинается с первой команды Ip в подпрограмме и заканчивается командой J(1, 1, p). При 1, 2, . . . проходах цикла в регистр R1 заносятся числа g(x1, . . . , xn, 0), g(x1, . . . , xn, 1), . . . . Затем командой J(1, ρ +n+ 2, q) эти числа сравнивается с неизменяемым нулем в регистре Rρ+n+2.
Поэтому, в общем случае, проверяется равенство g(x1, . . . , xn, k) = 0, и в этот момент в регистре Rρ+n+1 находится число k.