Различные методы решения неравенств. Общие методы решения неравенств

Общие методы решения неравенств

1. Обобщенный метод интервалов.
2. Метод замены переменной.
3. «Расщепление»

1. Обобщенный метод интервалов

Применимость метода интервалов не ограничивается решением рациональных

Алгоритм обобщенного метода интервалов

Привести неравенство к виду .
Найти область определения функции

Обобщенный метод интервалов. Примеры
3.

2.Метод замены переменной. Примеры.
1.
2.
3. log22( log0,5

3.«Расщепление» неравенств.

Если левая часть неравенства представляет собой произведение двух выражений,

«Расщепление» неравенств. Примеры.
1.
2.
3.

4.Использование свойств функции. 4.1. Исследование области определения функции.

Предварительный анализ области определения функций,

4.1. Исследование ОДЗ неизвестной. Примеры.
1.
2.
3.

4.2. Использование ограниченности функции. Метод оценки.

Иногда неравенство устроено так, что на всей

4.2. Использование ограниченности функции. Метод оценки.

Примеры.
1.
2.

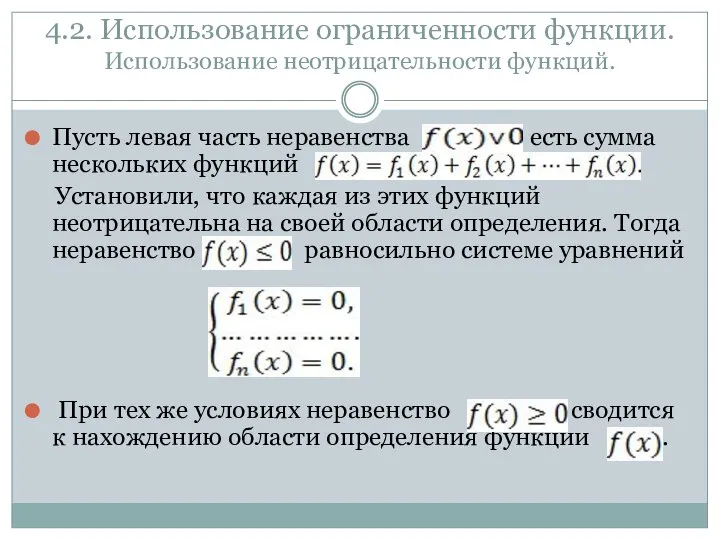
4.2. Использование ограниченности функции. Использование неотрицательности функций.

Пусть левая часть неравенства есть сумма

4.2. Использование ограниченности функции. Использование неотрицательности функций.

Примеры.
1.
2.

4.3. Использование монотонности функции.

Если функция возрастает на своей области определения, то

Использование монотонности. Примеры.

1.
2.
3.

5. Метод рационализации.

Метод рационализации заключается в замене сложного выражения F(x) на

Метод рационализации.

Метод рационализации. Примеры.

1.
2.
3.

Домашнее задание.

1.
2.
3.
4.
5.