Содержание
- 2. Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид aх +
- 3. Значение неизвестного, обращающее уравнение в верное равенство называется решением или корнем уравнения. Например, если в уравнении
- 4. Пример Решите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х ‒
- 6. Пусть надо решить уравнение 1) Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.
- 7. Вообще такие уравнения можно решать по следующей схеме: а) привести уравнение к целому виду; б) раскрыть
- 8. 1) 2х = 1/4. 2) 2 (х + 3) = 5 – 6х. 3) – 6
- 9. Методы решения систем уравнений
- 10. Системой уравнений называют два уравнения с двумя неизвестными (чаще всего неизвестные в них называют «x» и
- 11. Метод подстановки • Выражаем одну переменную через другую. • Выраженную из одного уравнения переменную подставляем во
- 13. Метод сложения • Добиваемся, путем равносильных преобразований, наличия равных (или противоположных) коэффициентов при одной из неизвестных
- 15. Графический метод решения систем уравнений
- 18. Скачать презентацию















 Порог чувствительности средства измерений
Порог чувствительности средства измерений Сфера и шар
Сфера и шар Решение задач по теории вероятности
Решение задач по теории вероятности Правила выполнения эскизов деталей средства и методы их измерения
Правила выполнения эскизов деталей средства и методы их измерения Своя игра. Математика 8 класс
Своя игра. Математика 8 класс Применение векторного и смешанного произведений в решении задач С2
Применение векторного и смешанного произведений в решении задач С2 Статистические характеристики. Среднее арифметическое, мода, медиана
Статистические характеристики. Среднее арифметическое, мода, медиана Решение задач с помощью уравнений
Решение задач с помощью уравнений Презентация на тему Нумерация многозначных чисел
Презентация на тему Нумерация многозначных чисел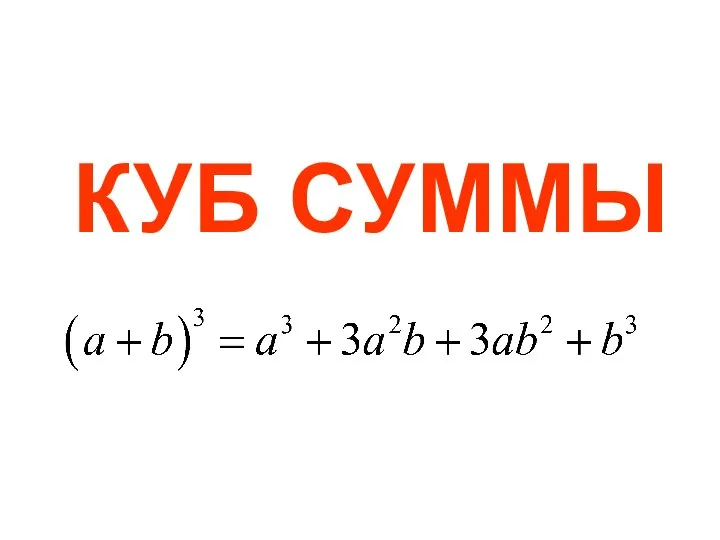 Куб суммы
Куб суммы Тренажёр. Римские числа
Тренажёр. Римские числа Векторы в пространстве. Урок 3-4
Векторы в пространстве. Урок 3-4 Презентация Площадь параллелограмма
Презентация Площадь параллелограмма  Первый урок алгебры в 7 классе
Первый урок алгебры в 7 классе Анализ вариационных рядов. Предмет и задачи математической статистики. (Глава 1.1)
Анализ вариационных рядов. Предмет и задачи математической статистики. (Глава 1.1) Деление с остатком (3 класс)
Деление с остатком (3 класс) Пропорциональные величины. Решение задач
Пропорциональные величины. Решение задач Көпбұрыштың ортогональ проекциясының ауданы
Көпбұрыштың ортогональ проекциясының ауданы Графический способ решения уравнений с модулем
Графический способ решения уравнений с модулем Числовые неравенства
Числовые неравенства Умножение. Координаты точки
Умножение. Координаты точки Сложение, вычитание, умножение дробей
Сложение, вычитание, умножение дробей Решение задач с помощью линейных уравнений
Решение задач с помощью линейных уравнений Математические понятия, предложения, доказательства
Математические понятия, предложения, доказательства Геометрический биатлон
Геометрический биатлон Алгоритм сложения и вычитания трёхзначных чисел. Растительный мир. Математика 3 класс. Урок 12
Алгоритм сложения и вычитания трёхзначных чисел. Растительный мир. Математика 3 класс. Урок 12 Антилогарифм
Антилогарифм Алгебраические дроби. 8 класс
Алгебраические дроби. 8 класс