Математический анализ Составитель: Никулина Л.С., старший преподаватель кафедры Математики и Моделирования
Содержание
- 2. Литература Основная литература: Л. Д. Кудрявцев. Курс математического анализа, т. 1, 2 Г. Н. Берман. Сборник
- 3. Дополнительная литература: Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики Данко П.Е., Попов А.Г.,
- 4. Учебно-методические разработки: Л. Я. Дубинина, Л. С. Никулина, И. В. Пивоварова. Курс лекций по высшей математике,
- 5. Содержание Функции нескольких переменных Дифференциальные уравнения 1-го, 2-го и более высокого порядков Кратные интегралы Числовые ряды
- 6. Функции нескольких переменных Лекция 1
- 7. Определение функции двух переменных Определение. Если каждой паре (x,y) значений двух независимых друг от друга переменных
- 8. Обозначения При этом пишут: Если паре соответствует число , то пишут Или называется частным значением функции
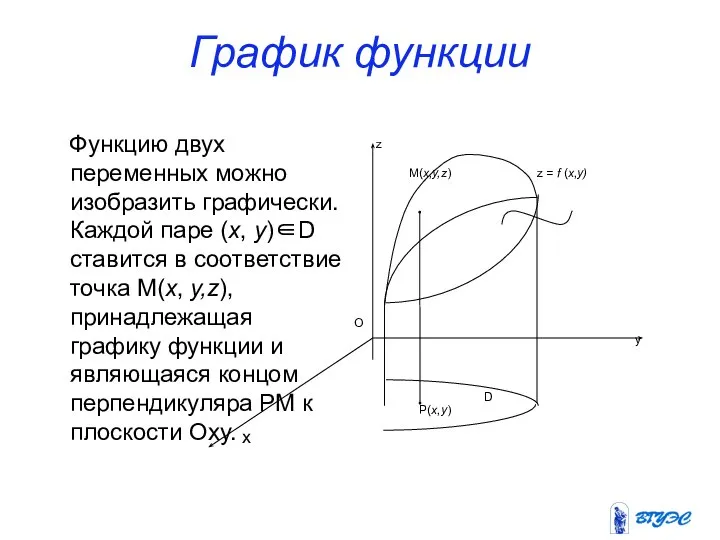
- 9. График функции 2-х переменных Геометрическое место точек, координаты которых удовлетворяют уравнению z= =f(x,y), называется графиком функции
- 10. График функции Функцию двух переменных можно изобразить графически. Каждой паре (x, y)∈D ставится в соответствие точка
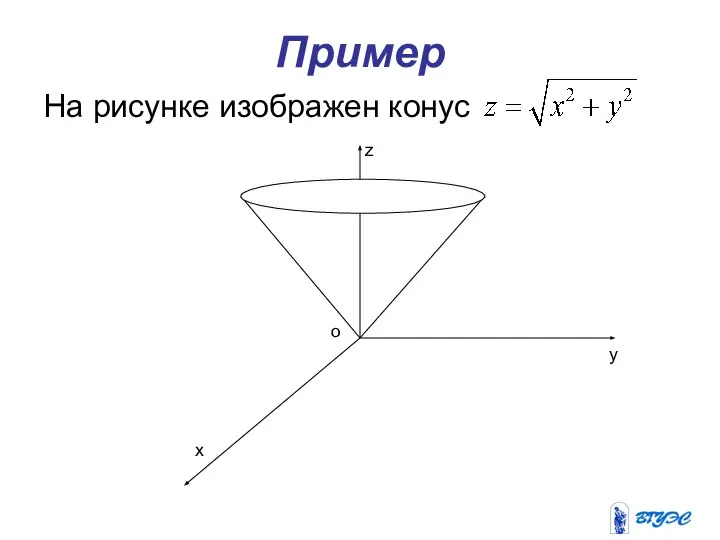
- 11. Пример На рисунке изображен конус x y z o
- 12. Предел функции 2-х переменных -окрестностью точки называется совокупность всех точек, лежащих внутри круга радиуса с центром
- 13. Предел функции 2-х переменных Таким образом, -окрестностью точки является множество точек, УДОВЛЕТВОРЯЮЩИХ НЕРАВЕНСТВУ . о х
- 14. Определение предела функции 2-х переменных Число А называется пределом функции z=f(x,y) при , если для любого
- 15. Функция нескольких переменных называется бесконечно малой, если ее предел равен нулю. Правила предельного перехода, установленные для
- 16. Непрерывность Функция z=f(x,y) называется непрерывной в точке , если выполнены условия: 1)функция определена в точке ,
- 17. Непрерывность Другое определение: Функция z=f(x,y) называется непрерывной в точке , если в этой точке бесконечно малому
- 18. Области Областью (открытой областью) называется множество точек плоскости, обладающее свойствами: каждая точка области принадлежит ей вместе
- 19. Точка называется граничной точкой области G, если любая окрестность этой точки содержит как точки области G,
- 20. Область называется ограниченной, если можно подобрать круг, полностью ее покрывающий. В противном случае область называется неограниченной
- 21. Функция называется непрерывной в области G, если она непрерывна в каждой точке этой области.
- 22. Свойства функции, непрерывной в замкнутой области Если функция непрерывна в ограниченной замкнутой области, то она в
- 23. Частные приращения функции 2-х переменных Разность = f (x+Δx, y) – f (x, y) называется частным
- 24. Частные производные Определение. Если существует = , то он называется частной производной (первого порядка) функции z
- 25. Аналогично определяется частная производная по переменной y: = Эту производную обозначают
- 26. Заметив, что вычисляется при неизменном y, а – при неизменном x, можно сделать вывод: правила вычисления
- 27. Производные высших порядков Частной производной n-го порядка функции нескольких переменных называется частная производная первого порядка от
- 29. Скачать презентацию
























 Неравенства. Тест
Неравенства. Тест Начала теории вероятности
Начала теории вероятности Перестановка слагаемых. (Урок 68)
Перестановка слагаемых. (Урок 68) Треугольник простейший и неисчерпаемый
Треугольник простейший и неисчерпаемый Тема: Конечные поля
Тема: Конечные поля Вынесение общего множителя за скобки
Вынесение общего множителя за скобки Числовая последовательность
Числовая последовательность Занятие по формированию элементарных математических представлений. Тема Насекомые
Занятие по формированию элементарных математических представлений. Тема Насекомые Из истории систем счисления
Из истории систем счисления Задача экономического содержания в ЕГЭ № 19
Задача экономического содержания в ЕГЭ № 19 Дискретная математика. Деревья. Определения дерева
Дискретная математика. Деревья. Определения дерева Среднее арифметическое
Среднее арифметическое Математика 1 класс. Определение форм
Математика 1 класс. Определение форм Поле чудес с животными
Поле чудес с животными  Многочлен и его стандартный вид
Многочлен и его стандартный вид Самая простая нерешенная задача
Самая простая нерешенная задача Формулы теории вероятностей
Формулы теории вероятностей Решение тригонометрических уравнений, сводящихся к квадратным
Решение тригонометрических уравнений, сводящихся к квадратным Фалес Милетский VI век до н. э. Теорема Фалеса
Фалес Милетский VI век до н. э. Теорема Фалеса Математический КВН
Математический КВН Сложение смешанных дробей
Сложение смешанных дробей ریاضی دوم دبستان فصل سوم :اشکال هندسی
ریاضی دوم دبستان فصل سوم :اشکال هندسی МАТЕМАТИКА 1 КЛАСС
МАТЕМАТИКА 1 КЛАСС  Трапеция. Свойства трапеции. Геометрия, 7 класс
Трапеция. Свойства трапеции. Геометрия, 7 класс Число пять на острове сокровищ
Число пять на острове сокровищ Признаки параллельности двух прямых
Признаки параллельности двух прямых Математика. Думать – коллективно!
Математика. Думать – коллективно! Умножение и деление десятичных дробей на натуральное число
Умножение и деление десятичных дробей на натуральное число