Содержание
- 2. The Bellman-Ford algorithm 1958 1962
- 3. The Bellman-Ford algorithm
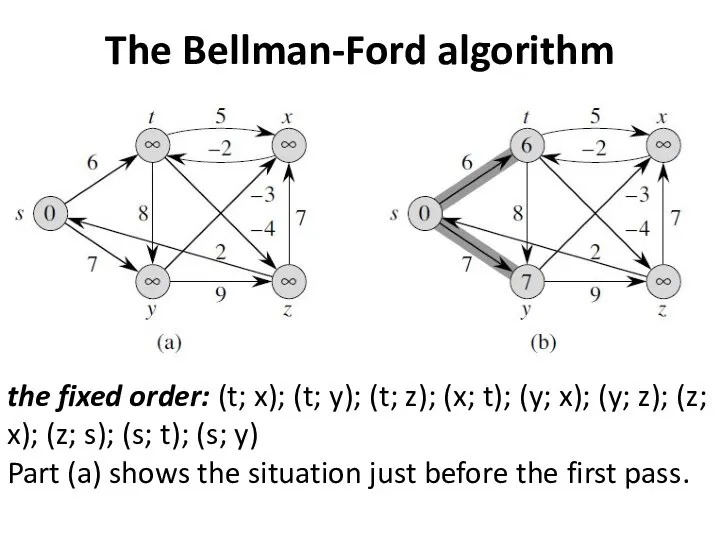
- 4. The Bellman-Ford algorithm the fixed order: (t; x); (t; y); (t; z); (x; t); (y; x);
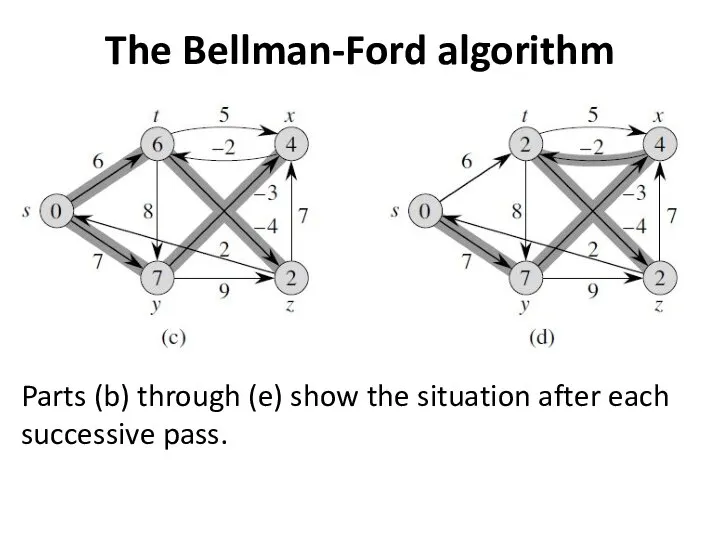
- 5. The Bellman-Ford algorithm Parts (b) through (e) show the situation after each successive pass.
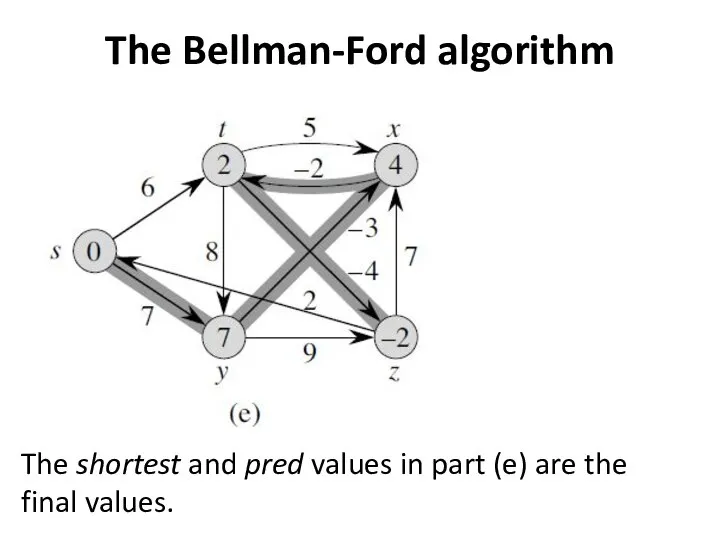
- 6. The Bellman-Ford algorithm The shortest and pred values in part (e) are the final values.
- 7. The Bellman-Ford algorithm Consider a shortest path from the source s to any vertex v. If
- 8. The Bellman-Ford algorithm Every acyclic path must contain at most n - 1 edges. If a
- 9. The Bellman-Ford algorithm The graph contains a negative-weight cycle and we have already run the BELLMAN-FORD
- 10. The Bellman-Ford algorithm How to find a negative-weight cycle, if one exists, after running BELLMAN-FORD? Go
- 12. The Bellman-Ford algorithm The loop of step 2 iterates n - 1 times. The loop of
- 13. The Bellman-Ford algorithm To find whether a negative-weight cycle exists taking O(m) time. If there is
- 14. The Bellman-Ford algorithm Negative-weight cycles relate to arbitrage opportunities in currency trading.
- 15. The Bellman-Ford algorithm n currencies c1; c2; c3; … ; cn, all the exchange rates between
- 16. The Bellman-Ford algorithm
- 17. The Bellman-Ford algorithm
- 18. The Bellman-Ford algorithm To find an arbitrage opportunity, if one exists, construct a directed graph with
- 19. The Bellman-Ford algorithm Add a new vertex s with a 0-weight edge (s; vi) to each
- 20. The Floyd-Warshall algorithm The classic example of all-pairs shortest paths is the table of a road
- 21. The Floyd-Warshall algorithm There is one problem with this example: it’s not all-pairs. If it were
- 22. The Floyd-Warshall algorithm What would be a rightful application of all-pairs shortest paths? Finding the diameter
- 23. The Floyd-Warshall algorithm Using the Floyd-Warshall algorithm, we can solve the all-pairs problem in Θ(n3) time.
- 24. The Floyd-Warshall algorithm The Floyd-Warshall algorithm relies on one property of shortest paths. If a shortest
- 25. The Floyd-Warshall algorithm the vertices are numbered from 1 to n Vertex numbers become important. shortest[u;
- 26. The Floyd-Warshall algorithm Let’s consider two vertices u and v. Pick a number x in the
- 27. The Floyd-Warshall algorithm There are two possibilities: First possibility: x is not an intermediate vertex in
- 28. The Floyd-Warshall algorithm adjacency-matrix representation The entry for edge (u; v) holds the weight of the
- 29. The Floyd-Warshall algorithm computes shortest[u; v; x] values => x=1 computes shortest[u; v; x] values =>
- 31. The Floyd-Warshall algorithm example shortest[2; 4; 0] is 1, because we can get from vertex 2
- 32. The Floyd-Warshall algorithm pred[u; v; 0] values
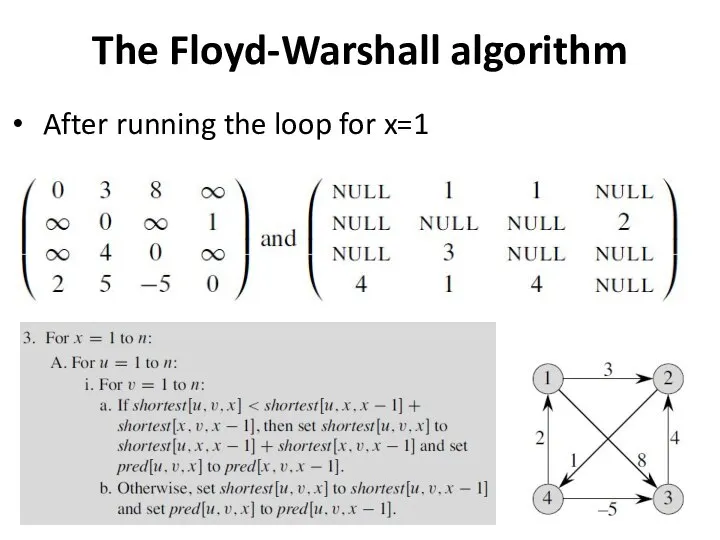
- 33. The Floyd-Warshall algorithm After running the loop for x=1
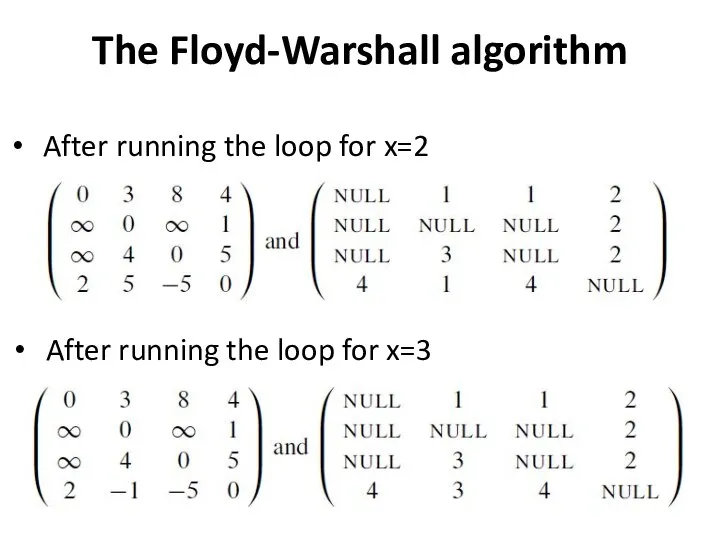
- 34. The Floyd-Warshall algorithm After running the loop for x=2 After running the loop for x=3
- 35. The Floyd-Warshall algorithm shortest[u; v; 4] and pred[u; v; 4] values
- 37. Скачать презентацию
























![The Floyd-Warshall algorithm computes shortest[u; v; x] values => x=1 computes](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1464658/slide-28.jpg)

![The Floyd-Warshall algorithm example shortest[2; 4; 0] is 1, because we](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1464658/slide-30.jpg)
![The Floyd-Warshall algorithm pred[u; v; 0] values](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1464658/slide-31.jpg)
![The Floyd-Warshall algorithm shortest[u; v; 4] and pred[u; v; 4] values](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1464658/slide-34.jpg)
 Наибольший общий делитель
Наибольший общий делитель Аттестационная работа. Эссе о включении учащихся в проектную деятельность на уроках математики
Аттестационная работа. Эссе о включении учащихся в проектную деятельность на уроках математики Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Устный счет. Арифметический корень натуральной степени
Устный счет. Арифметический корень натуральной степени Теорема Пифагора (теорема нимфы, теорема невесты)
Теорема Пифагора (теорема нимфы, теорема невесты) Основные понятия и определения графа и его элементов
Основные понятия и определения графа и его элементов Задачи на проценты 2
Задачи на проценты 2 Серединный перпендикуляр
Серединный перпендикуляр Аттестационная работа. Математическое общество учащихся Ориентир
Аттестационная работа. Математическое общество учащихся Ориентир Решение задач по теме «Векторы»
Решение задач по теме «Векторы» Булевы отношения
Булевы отношения Как путешествует точка? 6 класс
Как путешествует точка? 6 класс Аналитическая геометрия
Аналитическая геометрия Задача оптимизации
Задача оптимизации Алгебра передаточных функций
Алгебра передаточных функций Показатели вариации
Показатели вариации Презентация на тему Сложение и вычитание в пределах 20
Презентация на тему Сложение и вычитание в пределах 20  Математика в жизни человека Киреева Ольга и Пономарёва Анастасия ученицы 6 класса МБОУ ООШ с.Никольское.
Математика в жизни человека Киреева Ольга и Пономарёва Анастасия ученицы 6 класса МБОУ ООШ с.Никольское. В царстве чисел-великанов. (6 класс)
В царстве чисел-великанов. (6 класс) Решение тригонометрических уравнений функционально-графическим методом
Решение тригонометрических уравнений функционально-графическим методом Графики, уравнения, неравенства
Графики, уравнения, неравенства Формула разности квадратов. 7 класс
Формула разности квадратов. 7 класс Шар. Задачи
Шар. Задачи Пропорции и отношения
Пропорции и отношения Рисуем по координатам
Рисуем по координатам Сумма углов треугольника
Сумма углов треугольника Система линейных уравнений с двумя переменными
Система линейных уравнений с двумя переменными 8 способов решения квадратного уравнения. 8 класс
8 способов решения квадратного уравнения. 8 класс