Содержание
- 2. Система m линейных уравнений с n переменными имеет вид
- 3. В задачах линейного программирования представляют интерес системы, в которых ранг матрицы r системы A=(aij), i=1,2…m, j=1,2…n,
- 4. Любые m переменных системы m линейных уравнений с n переменными (m Тогда остальные n - m
- 5. Базисным решением системы m линейных уравнений с n переменными называется решение, в котором все n-m неосновных
- 6. Основными могут быть разные группы из n переменных. Максимальное число групп основных переменных
- 7. Пример. Найти все возможные группы основных переменных в системе
- 8. Решение системы называется допустимым, если оно содержит только неотрицательные компоненты, в противном случае – решение допустимое.
- 9. Базисным решением системы m линейных уравнений с n переменными называется решение, в котором все n-m неосновных
- 10. Пример. Найти все базисные решения системы
- 11. Симплексный метод решения задач линейного программирования
- 12. Решение любой задачи линейного программирования можно найти симплексным методом. Симплексный метод решения задачи линейного программирования основан
- 13. Оптимальный план - совокупность значений переменных, при которых достигается наибольшее или наименьшее значение целевой функции, любая
- 14. Для реализации симплексного метода необходимо освоить три основных элемента: Способ определения какого-либо первоначального допустимого базисного решения
- 15. Пусть требуется найти максимальное (минимальное) значение функции
- 16. при условиях
- 18. Алгоритм решения задачи симплексным методом: привести задачу линейного программирования к стандартному виду. найти начальное базисное решение
- 19. если выполняется критерий оптимальности решения, то решение задачи заканчивается если выполняется условие существования множества оптимальных решений,
- 20. Для нахождения первоначального базисного плана все переменные разбиваются на две группы: основные(базисные) и неосновные. Положив неосновные
- 21. Критерий оптимальности решения при отыскании максимума(минимума) линейной функции: Если в выражении линейной функции через неосновные переменные
- 22. Если система ограничений непротиворечива, то выполнение конечного числа последовательных шагов симплексного метода приводит к нахождению оптимального
- 23. Алгоритм решения задачи линейного программирования построением симплексной таблицы
- 24. Алгоритм: 1. Систему линейных неравенств записываем в каноническом виде. Для этого в каждое неравенство добавляем дополнительную
- 25. После введения добавочных переменных систему уравнений и линейную функцию записываем в виде:
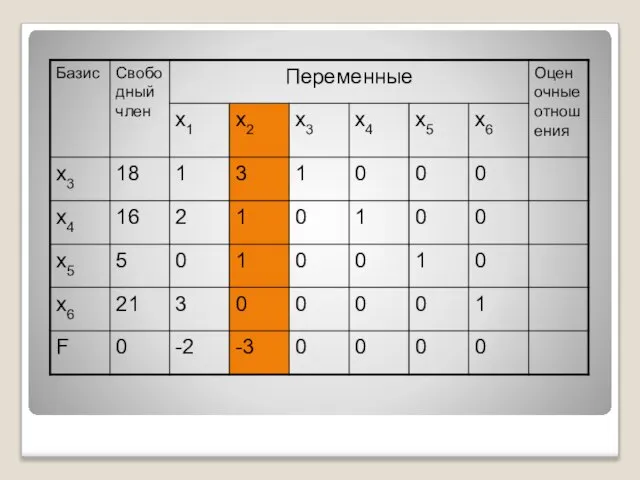
- 27. 2. Исходную расширенную систему заносим в первую симплексную таблицу.
- 29. 3. Проверяем выполнение критерия оптимальности при решении задач на максимум- наличие в последней строке отрицательных коэффициентов.
- 30. 4 Если критерий оптимальности не выполнен, то наибольший по модулю отрицательный элемент в последней строке определяет
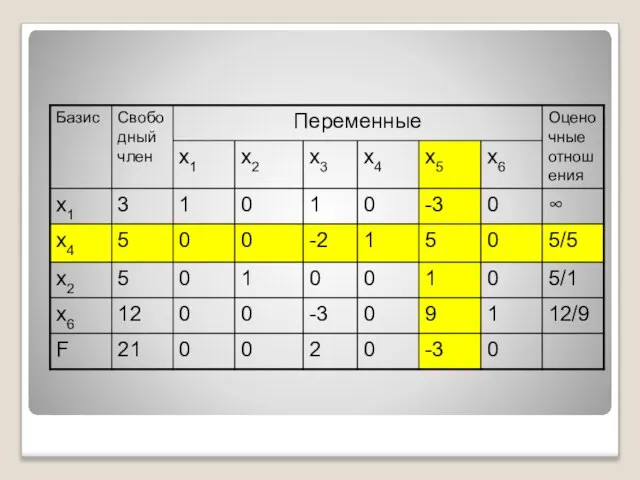
- 31. Составляем оценочные отношения каждой строки по правилам: ∞, если bi и ais имеют разные знаки; ∞,
- 32. Определяем
- 33. Если конечного минимума нет, то задача не имеет конечного оптимума (Fmax=∞) Если минимум конечен, то выбираем
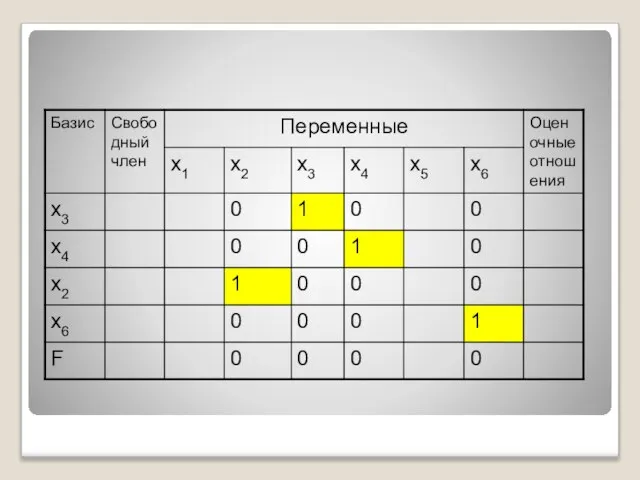
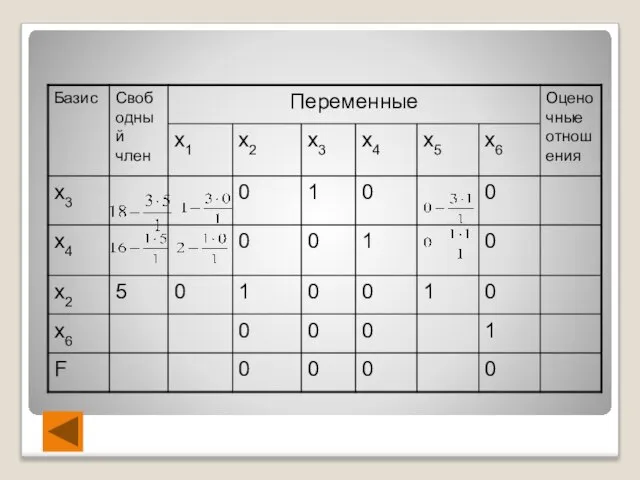
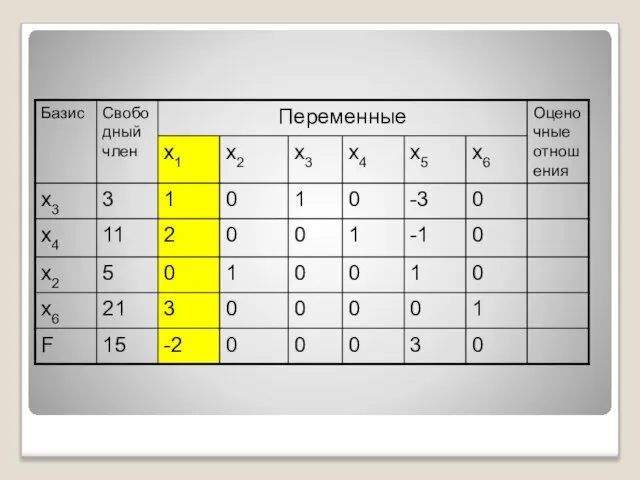
- 34. 5. Переходим к следующей таблице по правилам: в левом столбце записываем новый базис: вместо основной переменной
- 35. новую строку с номером q получаем из старой строки делением на разрешающий элемент aqs все остальные
- 36. Пример. Решим задачу об использовании ресурсов
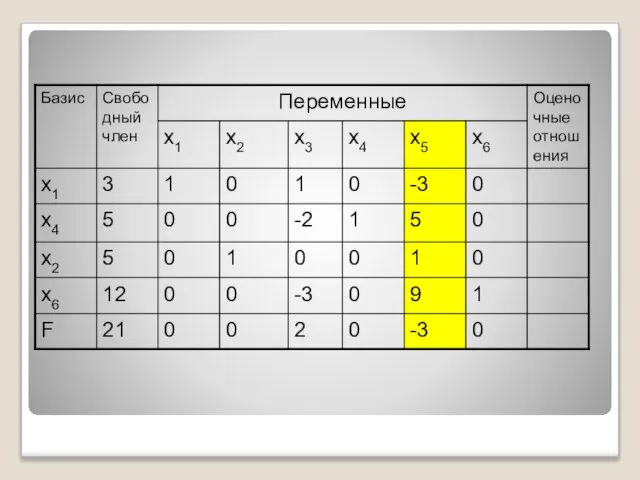
- 39. 1. Шаг
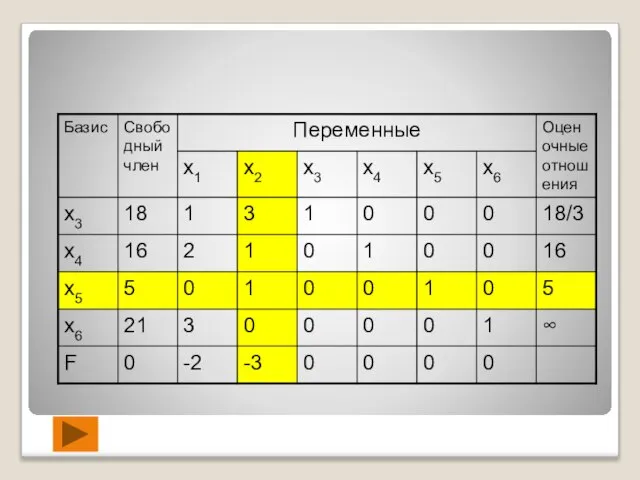
- 40. Заполняем первую симплексную таблицу, в которой переменные х3,х4,х5,х6 - основные
- 52. Скачать презентацию



































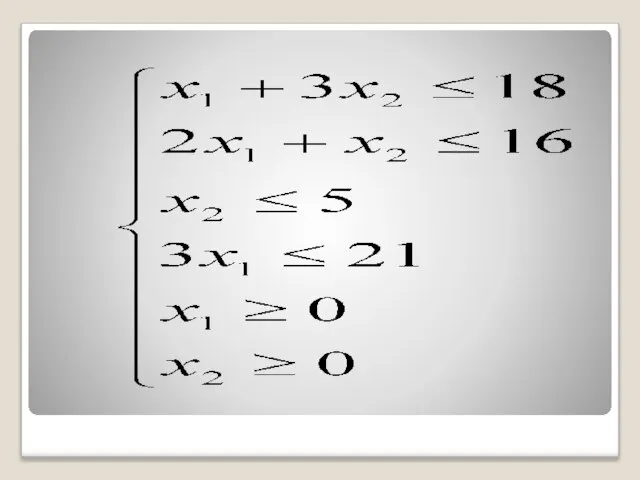
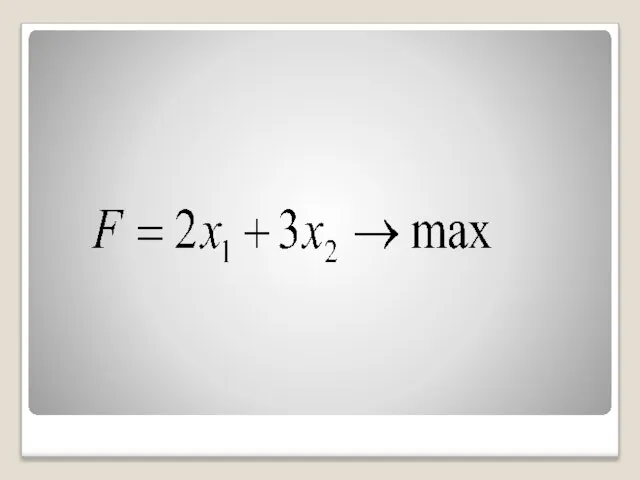
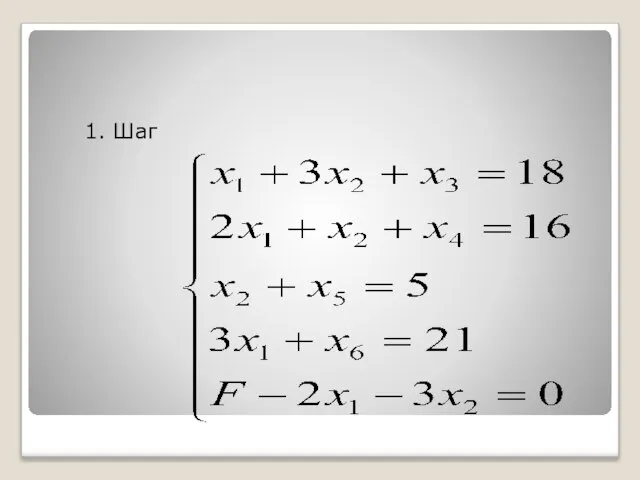




 Умножение одночленов. Возведение одночлена в степень
Умножение одночленов. Возведение одночлена в степень Прямоугольный параллелепипед
Прямоугольный параллелепипед Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Призма Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой
Призма Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой  Сложение чисел
Сложение чисел Решение примеров
Решение примеров Метод максимального правдоподобия
Метод максимального правдоподобия Основные этапы решения задач МПЭ
Основные этапы решения задач МПЭ Последовательности: путешествие вглубь веков
Последовательности: путешествие вглубь веков Таблица сложения однозначных чисел. 1 класс
Таблица сложения однозначных чисел. 1 класс ЕГЭ. Базовый уровень. Действия с дробями
ЕГЭ. Базовый уровень. Действия с дробями Решение задач на пропорциональное деление Урок 68
Решение задач на пропорциональное деление Урок 68 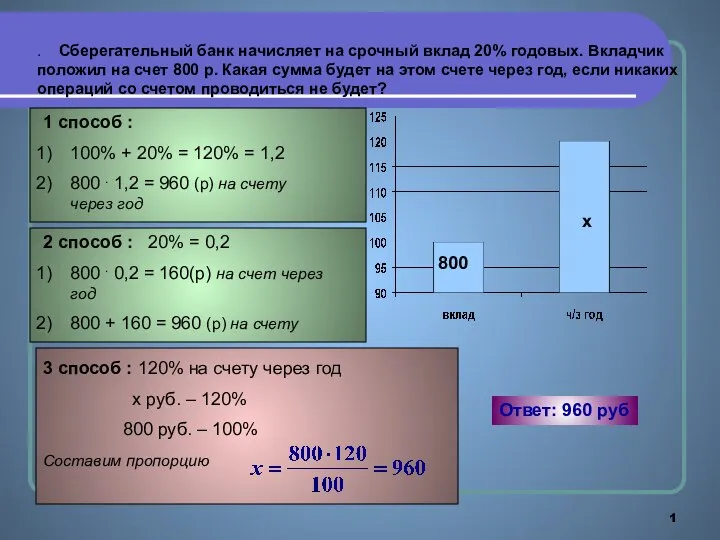 Задачи на проценты
Задачи на проценты Сравнение чисел. Урок математики в 6 классе
Сравнение чисел. Урок математики в 6 классе Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Где есть желание, найдётся путь МБОУ г. Астрахани «Лицей №3» 4 А класс
Где есть желание, найдётся путь МБОУ г. Астрахани «Лицей №3» 4 А класс  Решение планиметрических задач
Решение планиметрических задач Куб суммы
Куб суммы Презентация по математике "Призма" - скачать
Презентация по математике "Призма" - скачать  Вычитание натуральных чисел
Вычитание натуральных чисел Сложение и вычитание дробей с одинаковыми знаменателями. 5 класс
Сложение и вычитание дробей с одинаковыми знаменателями. 5 класс Математический язык. 7 класс
Математический язык. 7 класс Размещения. Повторение и закрепление пройденного материала
Размещения. Повторение и закрепление пройденного материала Основные теоремы и формулы планиметрии
Основные теоремы и формулы планиметрии Свойства четырехугольников. Решение задач
Свойства четырехугольников. Решение задач Презентация по математике "Сравнение чисел в ГИА" - скачать бесплатно
Презентация по математике "Сравнение чисел в ГИА" - скачать бесплатно Методи розподілу витрат на змінну та постійну частини. (Тема 4)
Методи розподілу витрат на змінну та постійну частини. (Тема 4) Освобождение от иррациональности в знаменателе
Освобождение от иррациональности в знаменателе