Содержание
- 2. Содержание 1.Некоторые сведения о многочленах 2. Интегрирование дробно-рациональных функций. 3. Интегрирование тригонометрических функций. 4. Интегрирование простейших
- 3. Некоторые сведения о многочленах
- 4. Понятие многочлена Функция , где n–целое число, называется многочленом или рациональной целой функцией от x. Число
- 5. Теорема Безу Число a является корнем многочлена тогда и только тогда, когда многочлен делится на x–a
- 6. Доказательство Если многочлен степени n разделить на x–a, то очевидно в частном получится многочлен степени ,
- 7. Доказательство Обратно, если r=0, то при x=a правая часть (*) обращается в нуль, тогда и ,
- 8. Теоремы алгебры Теорема .Всякий многочлен степени имеет по крайней мере один корень. Теорема. Всякий многочлен степени
- 9. Случай кратных действительных корней Если в разложении многочлена на множители некоторые линейные множители окажутся одинаковыми, то
- 10. Пример . Корень –двукратный корень этого многочлена, –простой корень.
- 11. Случай комплексных корней Теорема. Всякий многочлен n–ой степени имеет ровно n корней (действительных или комплексных). Теорема.
- 12. Продолжение Итак, в разложении многочлена на множители комплексные корни входят попарно сопряженными.Им соответствует множитель вида где
- 13. Случай кратных комплексных корней Если комплексные корни многочлена являются кратными, то этот многочлен с действительными коэффициентами
- 14. Интегрирование рациональных дробей
- 15. Рациональные дроби Рациональной дробью называется выражение вида , где - многочлены степеней n и m соответственно.
- 16. Рациональные дроби Если рациональная дробь является неправильной, то произведя деление на по правилу деления многочленов, ее
- 17. Простейшие рациональные дроби Правильные рациональные дроби вида где k–целое положительное число ≥2, дискриминант квадратного трехчлена отрицателен,
- 18. Интегрирование простейших рациональных дробей Дробь 1-го типа: Дробь 2-го типа:
- 19. Пример интегрирования рациональной дроби Найдем Разложим знаменатель дроби на множители: Тогда Приведем дроби к общему знаменателю
- 20. Продолжение Положим в обеих частях этого тождества х=0. Получим 8=4А. Тогда А=2. При х=-2 20=-2С, а
- 21. Продолжение
- 22. Пример интегрирования рациональной дроби Вычислить Приведем выражение к общему знаменателю: .
- 23. Приравняем числители . Многочлены, стоящие в правой и левой частях этого соотношения тождественно равны, т. е.
- 24. Продолжение Отсюда получаем: С=1, D=0, А=-3, В=0. Следовательно, подставляя найденные коэффициенты в разложение дроби на простейшие,
- 25. Продолжение
- 26. Интегрирование тригонометрических функций
- 27. Интегралы вида Если хотя бы одно из чисел m или n - нечетное положительное число, то
- 28. Примеры Вычислить . Отделим от нечетной степени косинуса один множитель, внесем под знак дифференциала синус и
- 29. Продолжение 2. Интегралы вида где m и n – четные положительные числа, вычисляют с помощью формул
- 30. Пример
- 31. Продолжение 3.Интегралы вида вычисляют преобразованием произведения тригонометрических функций в сумму по формулам:
- 32. Пример Рассмотрим пример: =
- 33. Продолжение 4. Интегралы где вычисляют заменой Второй интеграл берут с помощью подстановки t=ctgx.
- 34. Пример Вычислим: Разложим интеграл на два интеграла..Получим
- 35. Продолжение 5.Такой же заменой можно брать интегралы целые числа одинаковой четности. Например,
- 36. Универсальная подстановка 6. Интегралы берут с помощью универсальной подстановки Откуда Например,
- 37. Продолжение 7. Универсальная подстановка приводит к громоздким выкладкам! Поэтому если R(sinx,cosx)=R(-sinx,-cosx), то удобнее пользоваться подстановкой tgx=t.
- 38. Пример
- 39. Интегрирование простейших иррациональностей
- 40. Иррациональность, содержащая квадратный трехчлен 1.Интегралы вида берут, выделяя полный квадрат и вводя новую переменную.
- 41. Продолжение 2. Интегралы вида вычисляют с помощью подстановки Интегралы вида вычисляют с помощью подстановки где n–наименьшее
- 42. Тригонометрические подстановки Интегралы вида вычисляют с помощью тригонометрических подстановок. 1.
- 43. Тригонометрические подстановки 2. 3.
- 45. Скачать презентацию










































 Упрощение выражений (2)
Упрощение выражений (2) Симметрия вокруг нас
Симметрия вокруг нас Задачи на проценты
Задачи на проценты Решение логарифмических уравнений
Решение логарифмических уравнений  Презентация "Решение уравнений (7 класс)" - скачать
Презентация "Решение уравнений (7 класс)" - скачать  Подготовка к ЕГЭ по математике. Решение заданий В12
Подготовка к ЕГЭ по математике. Решение заданий В12 Решение задач на деление дробей
Решение задач на деление дробей Математика – симфония чисел
Математика – симфония чисел Производная функции
Производная функции Извлечение квадратного корня
Извлечение квадратного корня Теория антагонистических игр. Задачи для выполнения
Теория антагонистических игр. Задачи для выполнения Система линейных уравнений с двумя переменными
Система линейных уравнений с двумя переменными Кейс №2. Формализованные методы прогнозирования
Кейс №2. Формализованные методы прогнозирования Натуральный ряд. Последовательные числа и порядок действий
Натуральный ряд. Последовательные числа и порядок действий Решение задач на применение теоремы Пифагора
Решение задач на применение теоремы Пифагора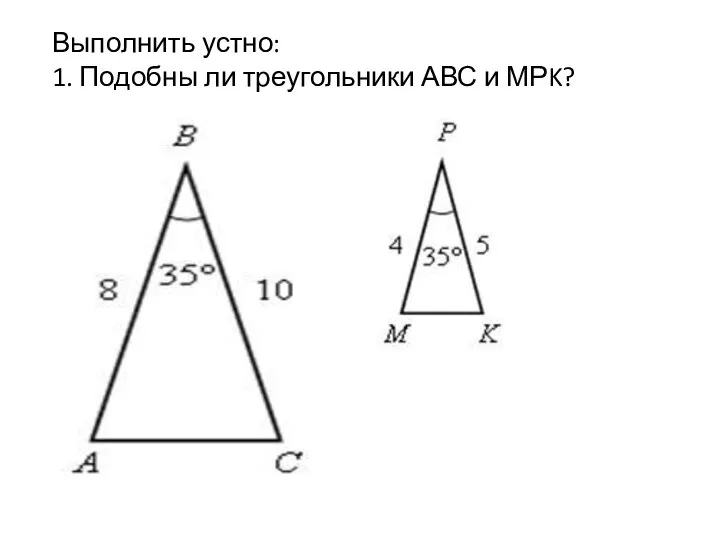 Признаки подобия треугольников. Урок 34
Признаки подобия треугольников. Урок 34 Теорема Пифагора
Теорема Пифагора Функция. Область определения и множество значений функции
Функция. Область определения и множество значений функции Математика на службе армии. С Днем Защитника Отечества! 10 класс
Математика на службе армии. С Днем Защитника Отечества! 10 класс Корреляциялық талдау
Корреляциялық талдау Методические рекомендации по заданию 14. Метод рационализации
Методические рекомендации по заданию 14. Метод рационализации Возрастание и убывание функции. Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.
Возрастание и убывание функции. Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.  Математические модели и методы
Математические модели и методы Исследовательский проект: Поиск выигрышной стратегии при решении задач Выполнили работу: Сергеева К. Евграфова К. Кудрявцева
Исследовательский проект: Поиск выигрышной стратегии при решении задач Выполнили работу: Сергеева К. Евграфова К. Кудрявцева  Умножение десятичных дробей. Устный счёт
Умножение десятичных дробей. Устный счёт Противоположные числа. Модуль числа
Противоположные числа. Модуль числа Леонардо по прозвищу Фибоначчи
Леонардо по прозвищу Фибоначчи Сравнение многозначных чисел
Сравнение многозначных чисел