Содержание
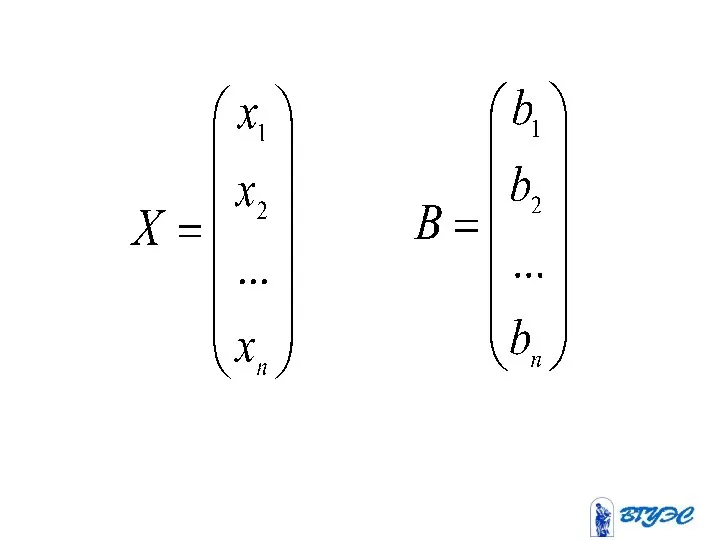
- 3. Здесь - неизвестные; - коэффициенты при неизвестных, где - номер уравнения, - номер неизвестного; - свободные
- 4. Система наз. неоднородной, если не все равны нулю. Система наз. однородной, если все равны нулю.
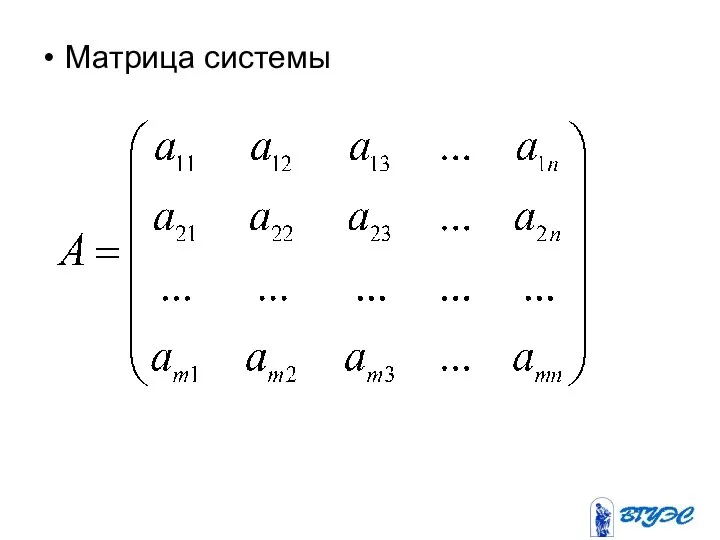
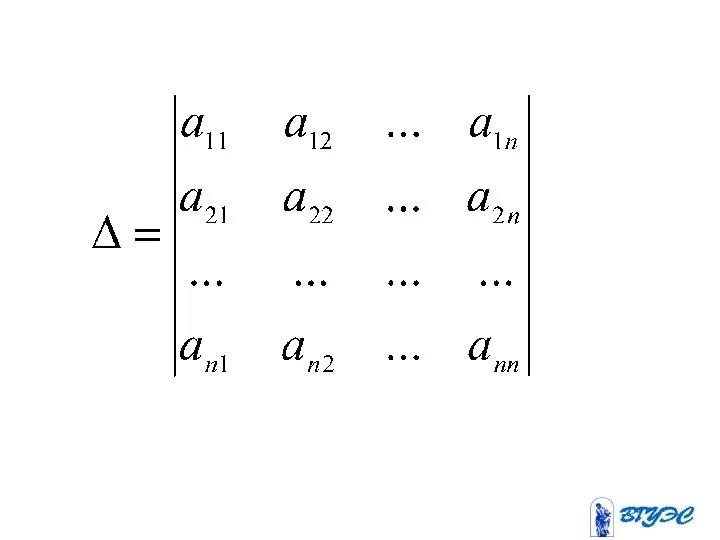
- 5. Матрица системы
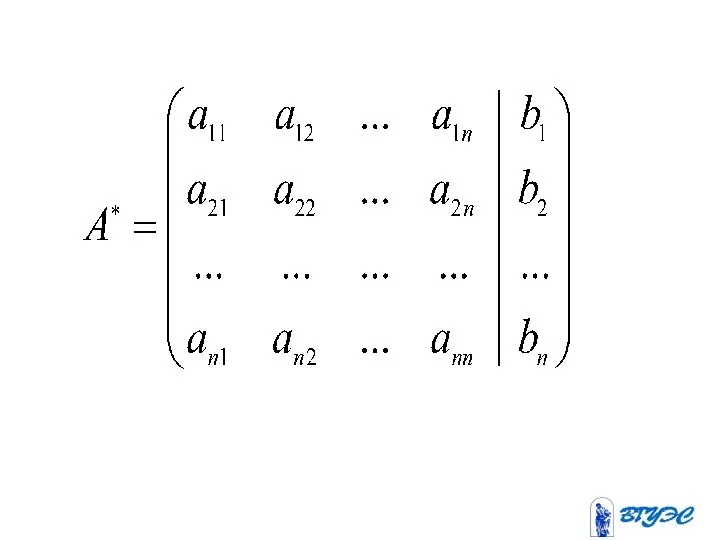
- 6. Расширенная матрица
- 7. Решением системы будем называть упорядоченный набор чисел обращающий каждое уравнение системы в верное равенство.
- 8. Решить систему — значит найти все ее решения или доказать, что ни одного решения нет. Система,
- 9. Если система не имеет решений, то она называется несовместной. Система, имеющая более чем одно решение, называется
- 10. Две системы, множества решений которых совпадают, называются эквивалентными или равносильными. Преобразование, применение которого превращает систему в
- 11. Метод Гаусса
- 12. Рассмотрим квадратную систему:
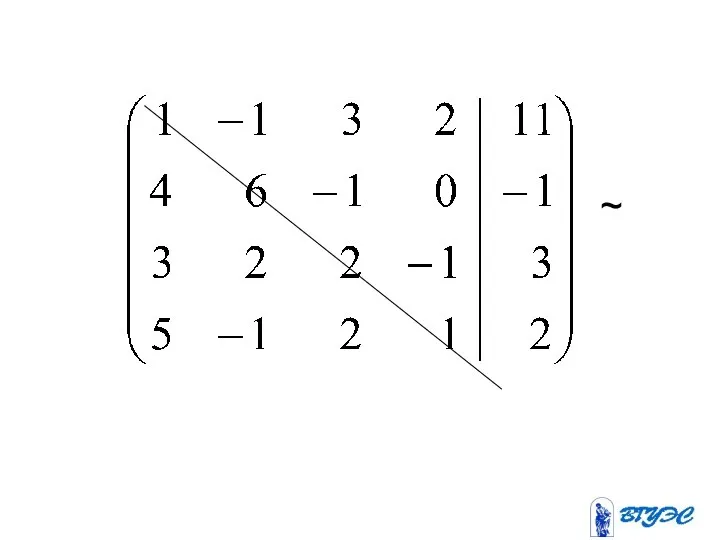
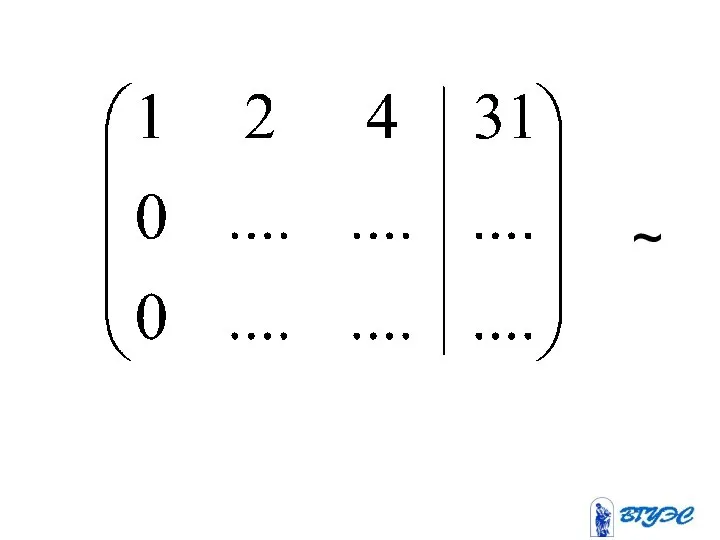
- 13. ~
- 14. ~
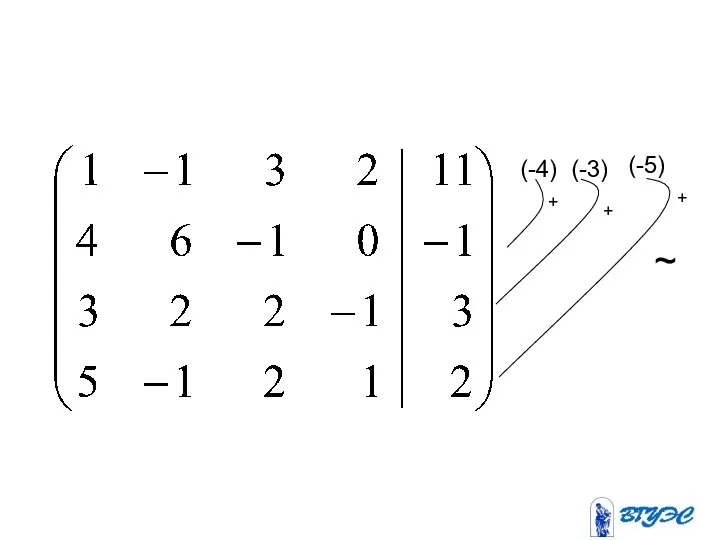
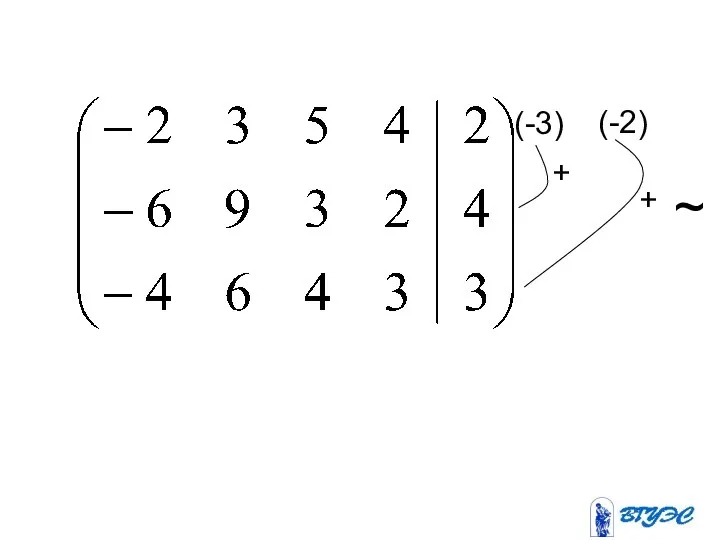
- 15. ~ (-4) (-3) (-5) + + +
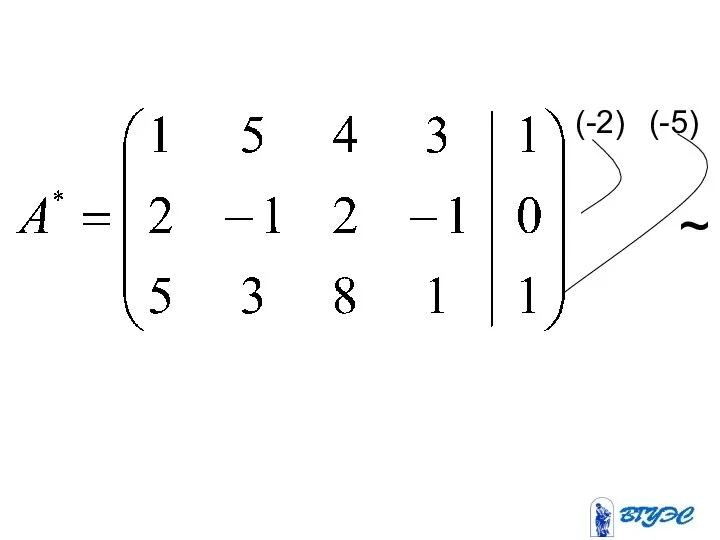
- 16. (-2) (-5) 2 + +
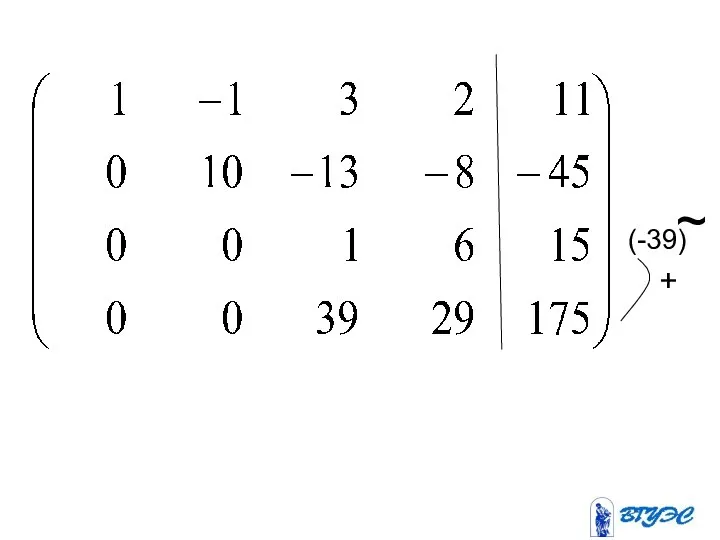
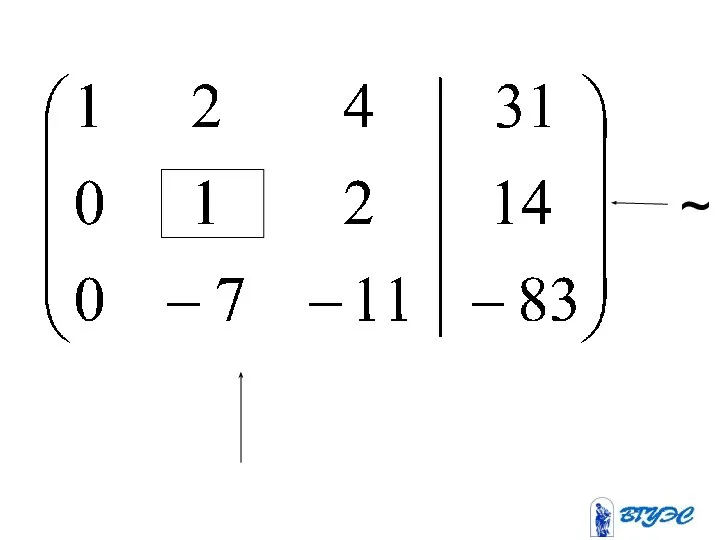
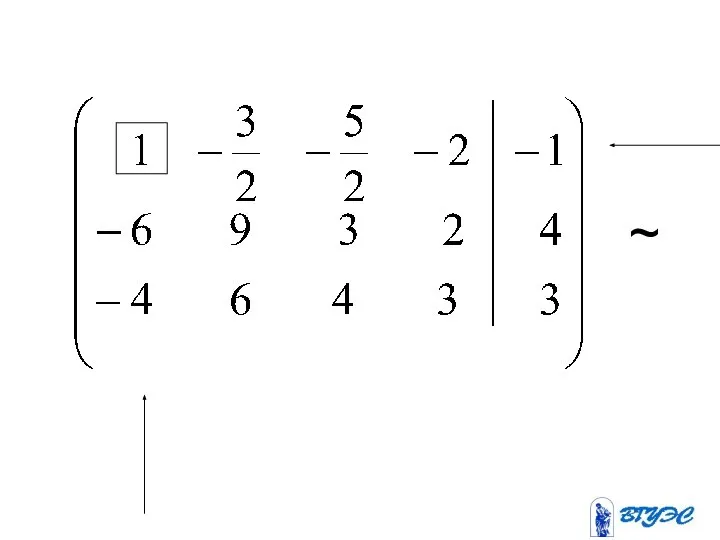
- 17. (-39) + ~
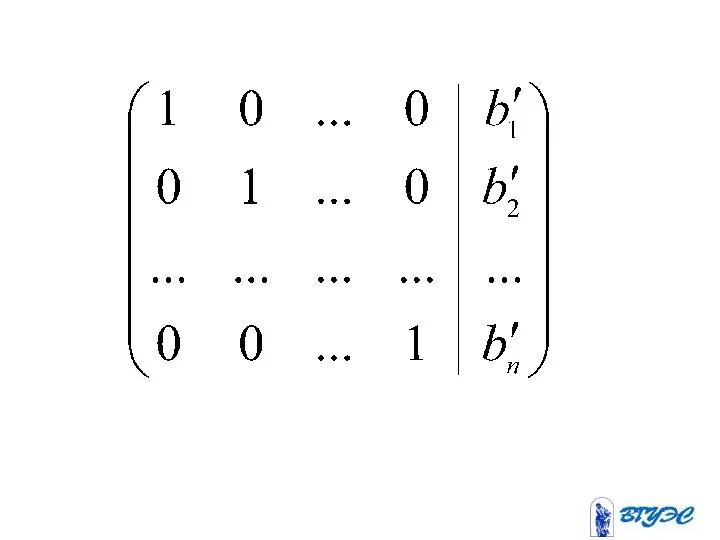
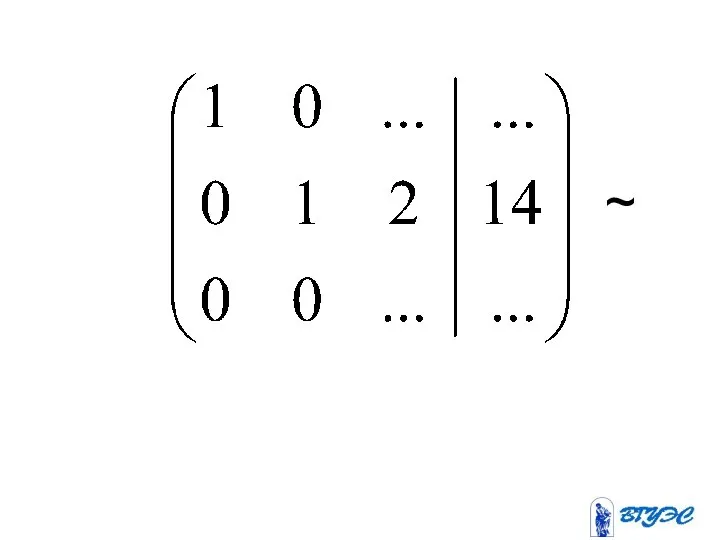
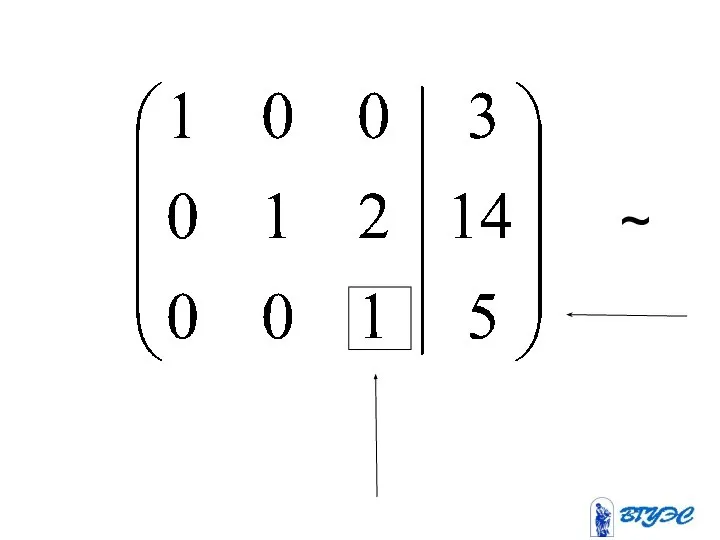
- 19. Полученная матрица соответствует системе:
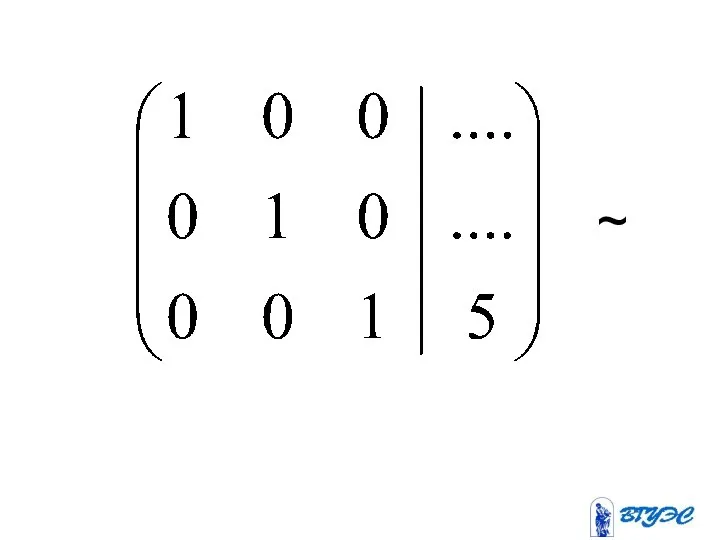
- 22. ~
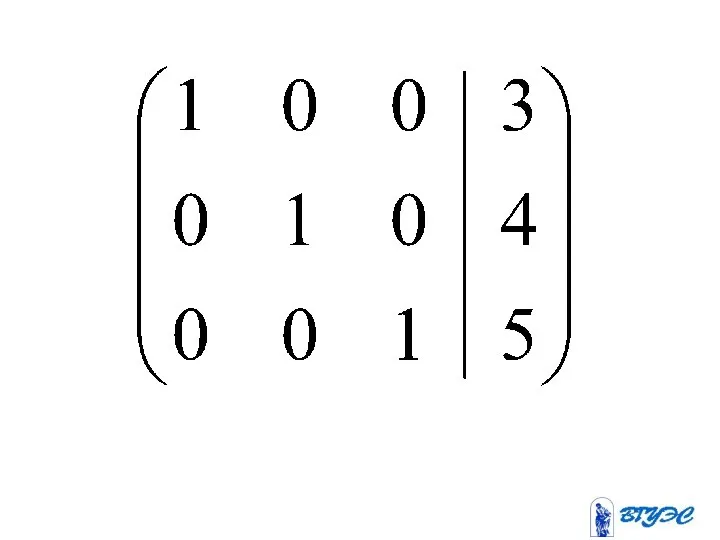
- 23. (-3) (-2) + + ~
- 24. ~
- 25. (-2) + ~
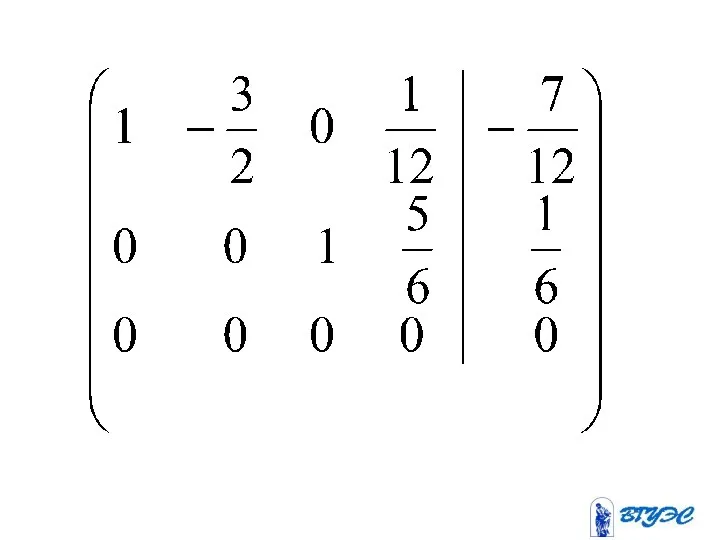
- 26. ~
- 28. Рассмотрим минор назовем его базисным. Тогда базисные переменные.
- 34. Метод Жордана-Гаусса
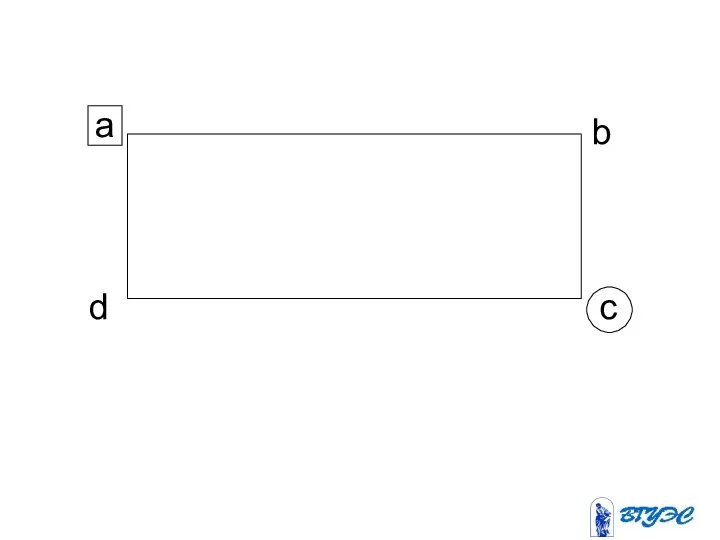
- 40. a c b d
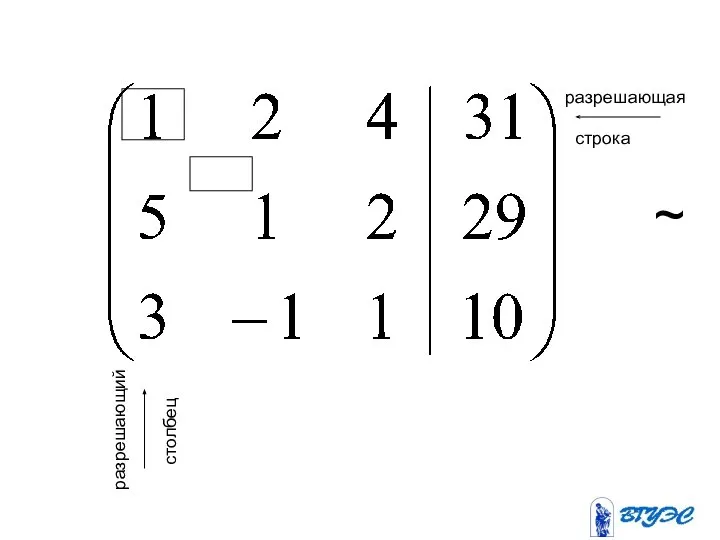
- 42. разрешающая разрешающий строка столбец ~
- 43. ~
- 44. ~
- 45. ~
- 46. ~
- 47. ~
- 48. ~
- 49. ~
- 50. ~
- 54. ~
- 55. ~
- 56. ~
- 57. ~
- 58. ~
- 59. ~
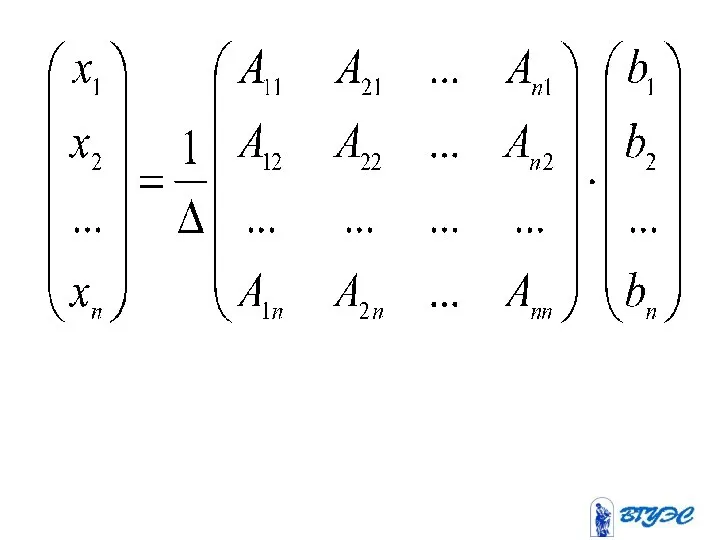
- 64. Матричный метод
- 65. С помощью этого метода можно решать квадратные системы линейных уравнений
- 67. Систему можно записать в виде где (1)
- 69. Если матрица невырожденная, то можно выполнить преобразования (2)
- 81. Метод Крамера
- 82. Если определитель системы линейных уравнений с неизвестными отличен от нуля, то эта система является определенной и
- 85. Здесь – определитель, получающийся из определителя заменой i-го столбца столбцом свободных членов.
- 96. Если и по крайне мере один из определителей , то система не имеет решения. Если и
- 100. Система не имеет решения, т.к. первое и третье уравнения противоречивы
- 104. Второе уравнение получается умножением первого на два. Данная система равносильна системе Система имеет бесчисленное множество решений.
- 108. Т е о р е м а К р о н е к е р а
- 109. Замечание. Пусть система совместна и если число уравнений равно числу неизвестных, причем , то система имеет
- 110. (-2) (-5) ~
- 111. (-2) ~
- 114. Однородные системы
- 116. Скачать презентацию
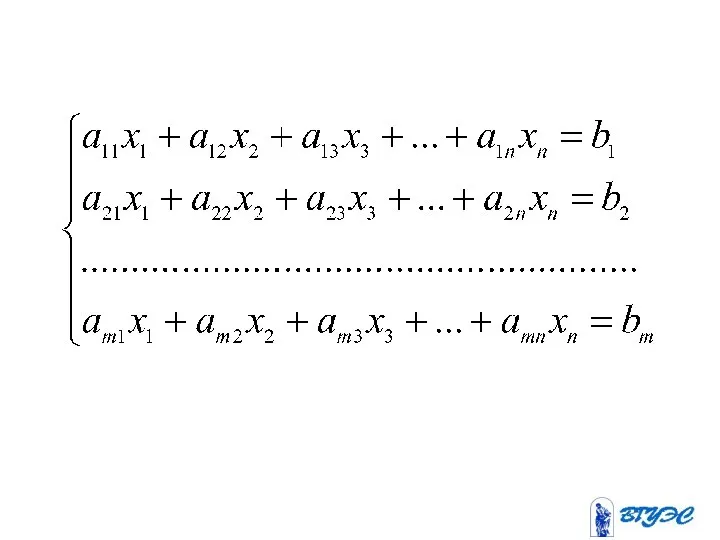










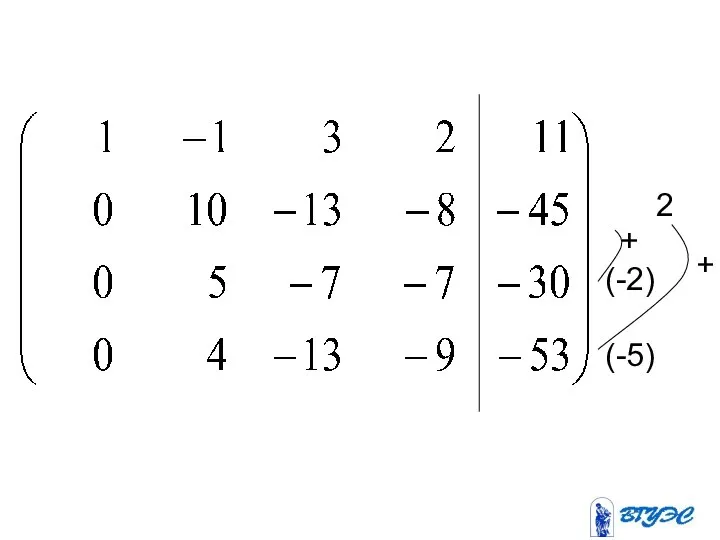


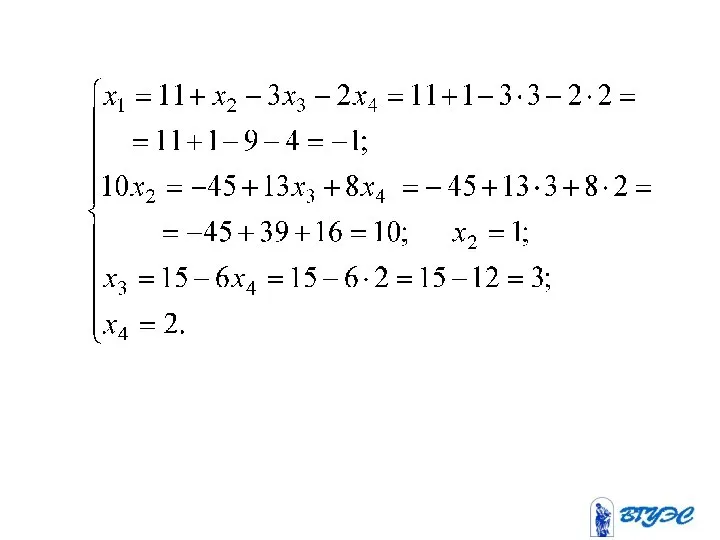
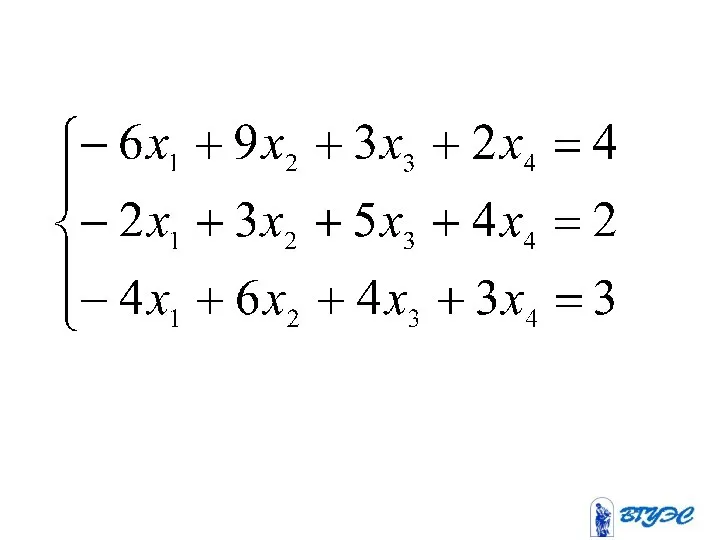
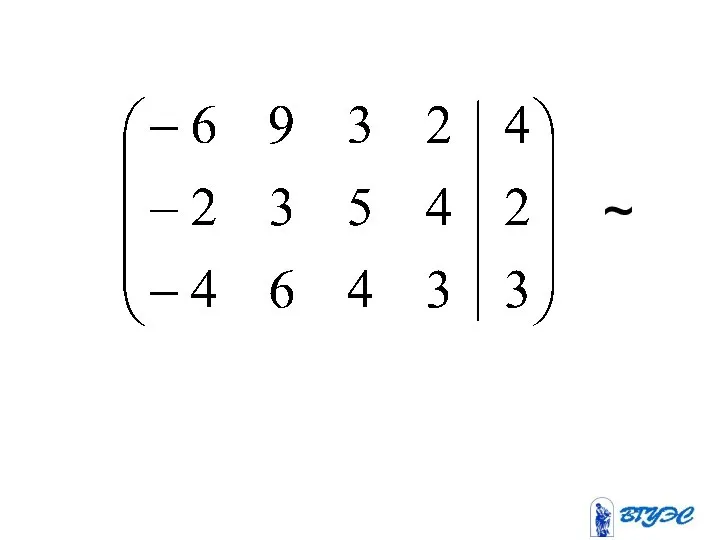
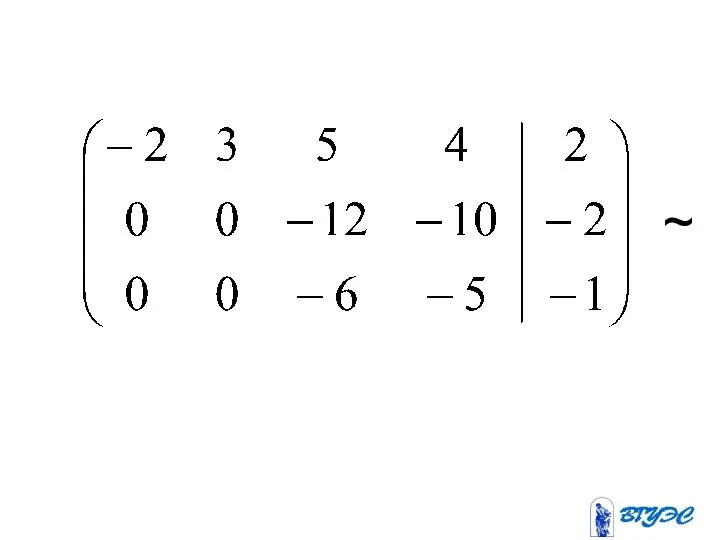
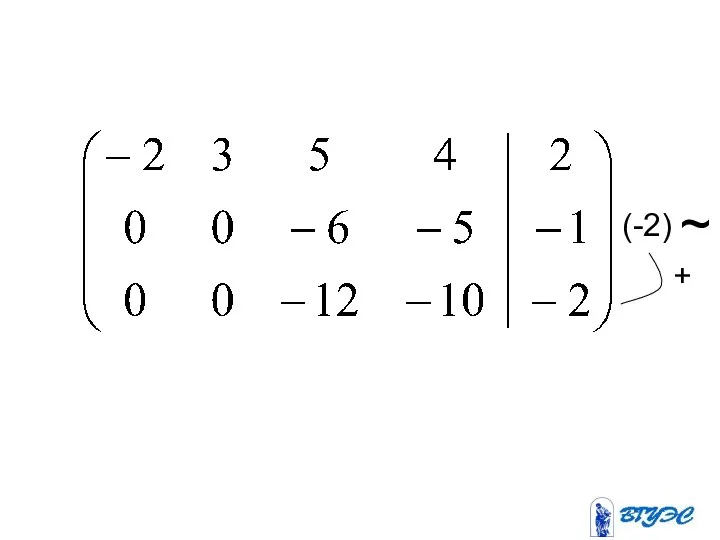



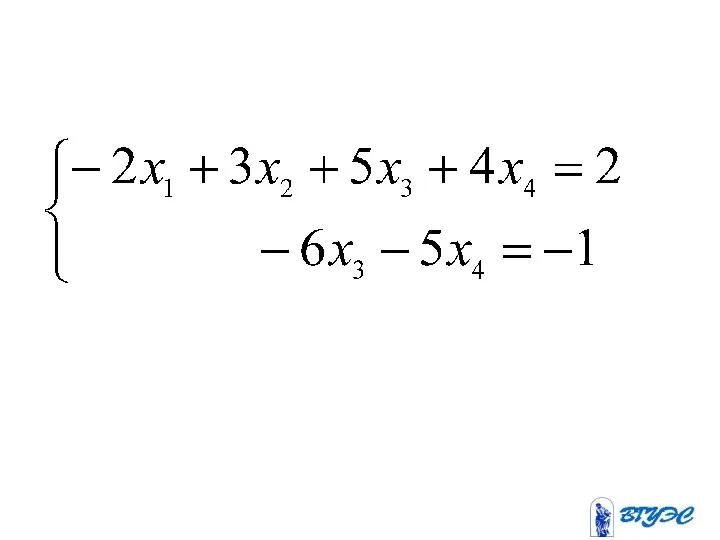
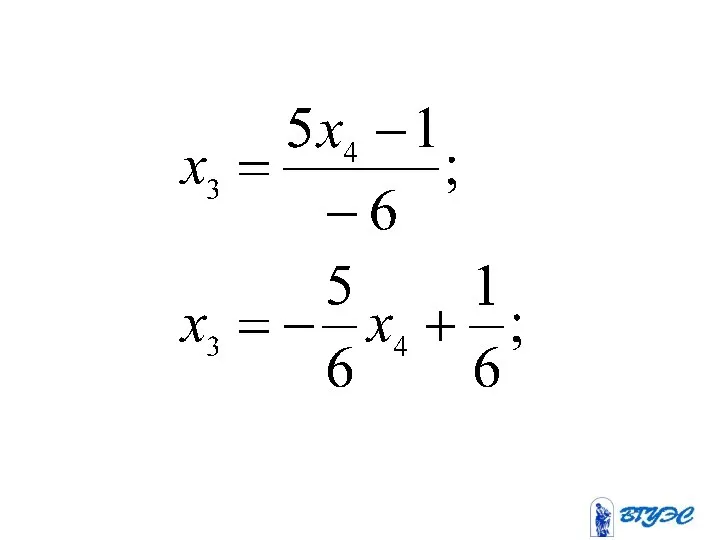
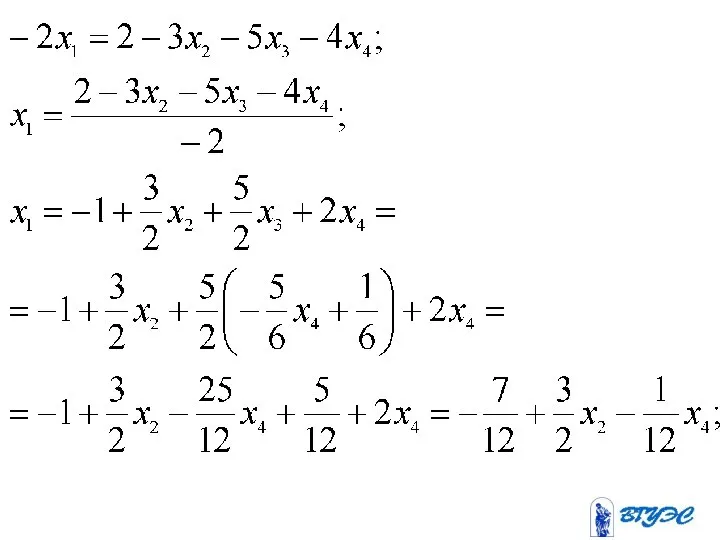
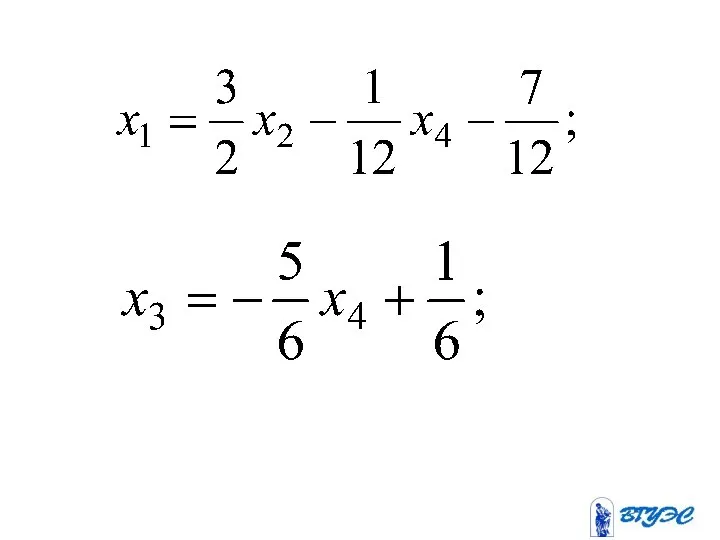
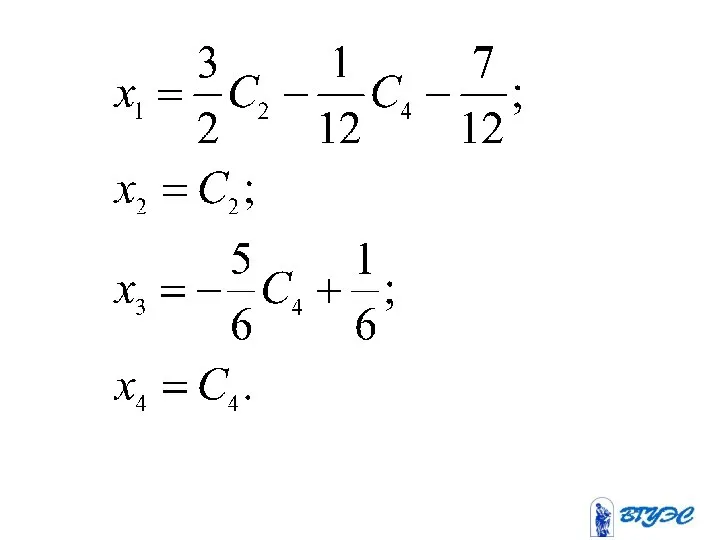

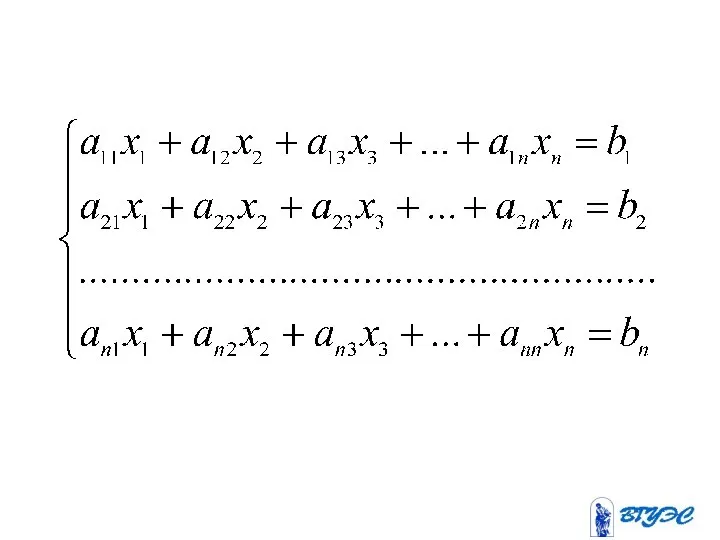
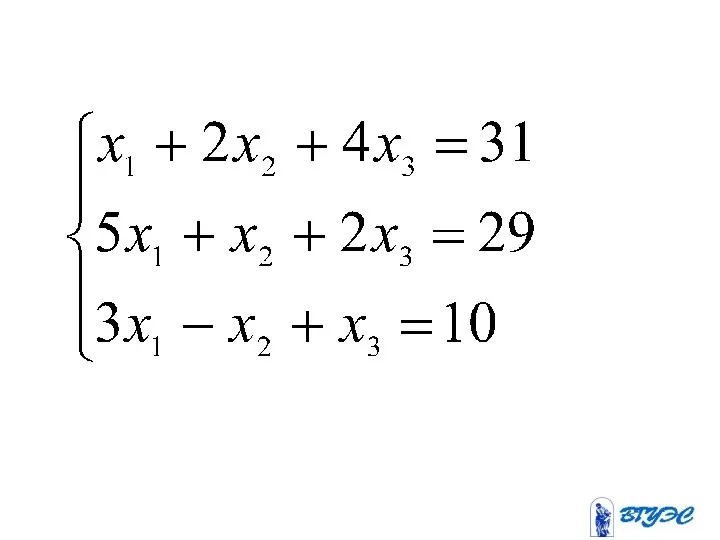

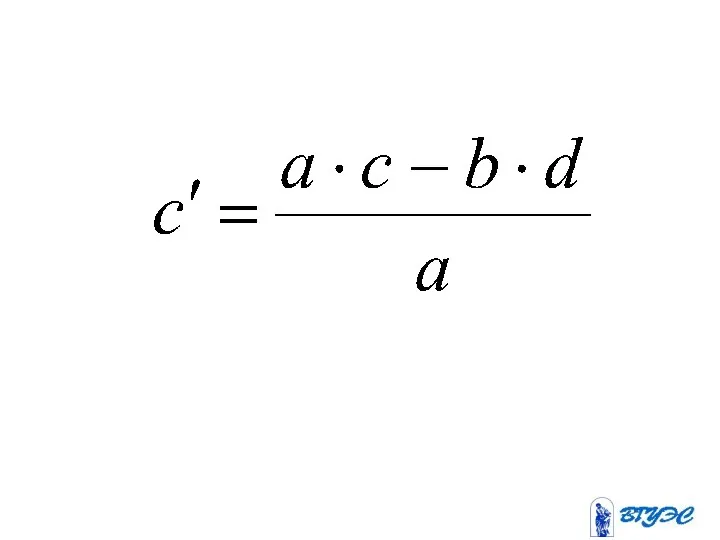

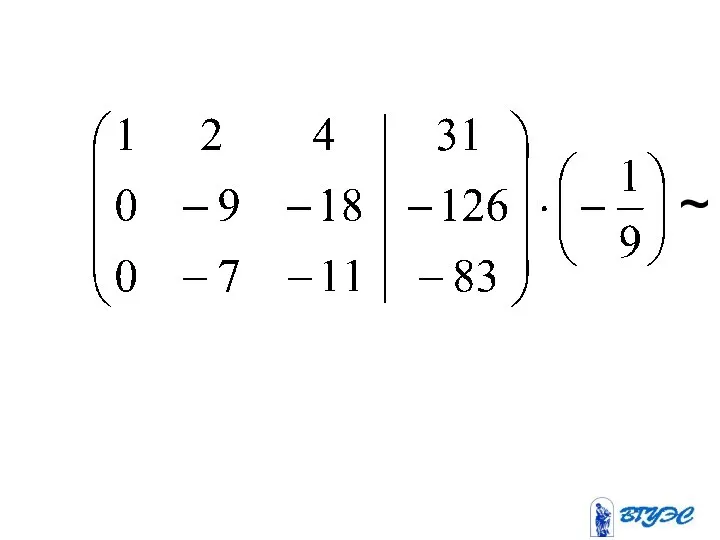
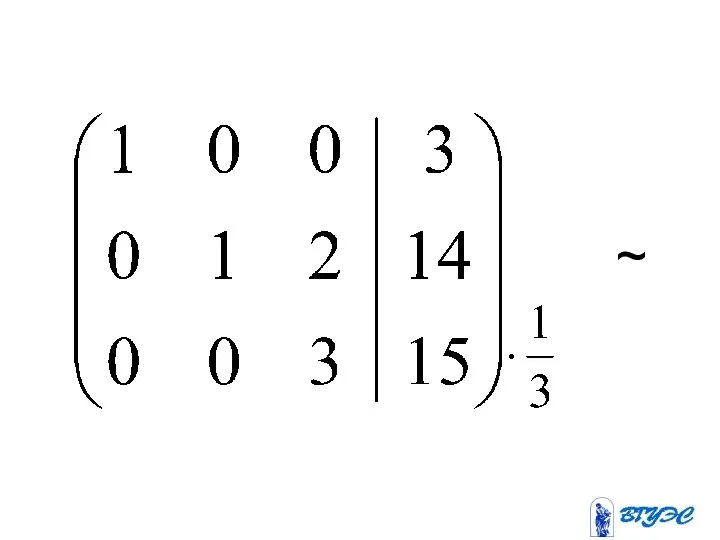
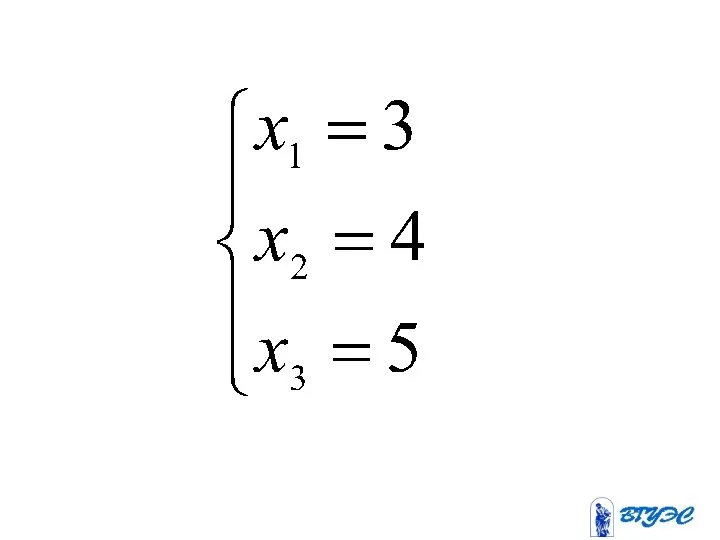
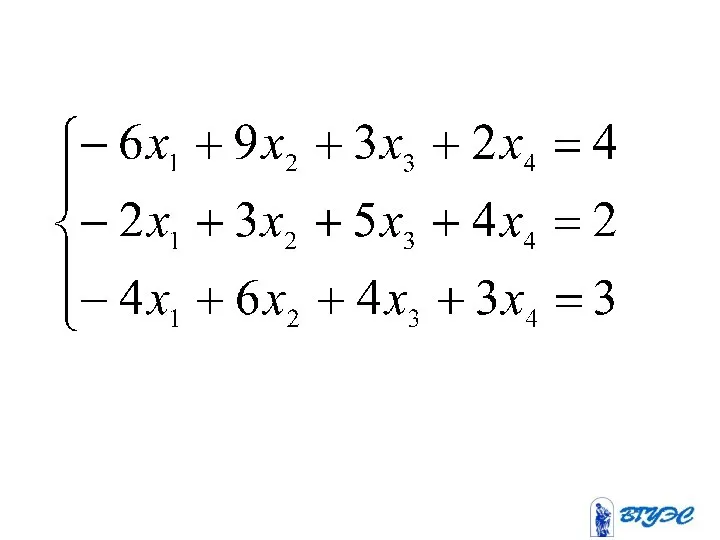

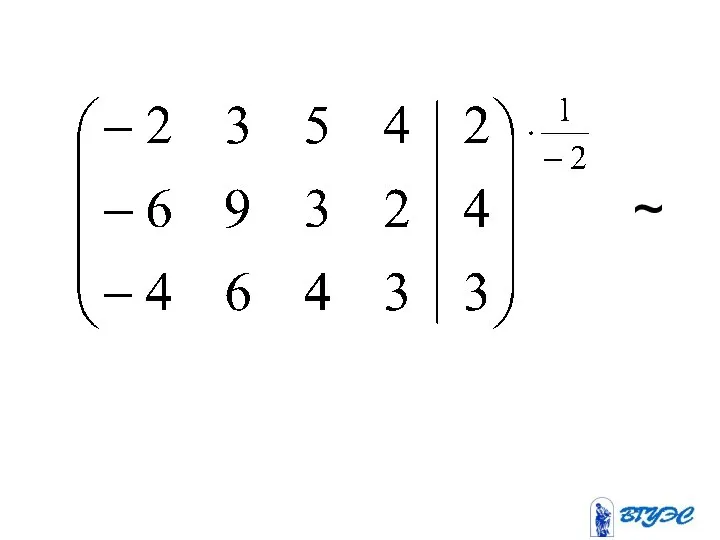
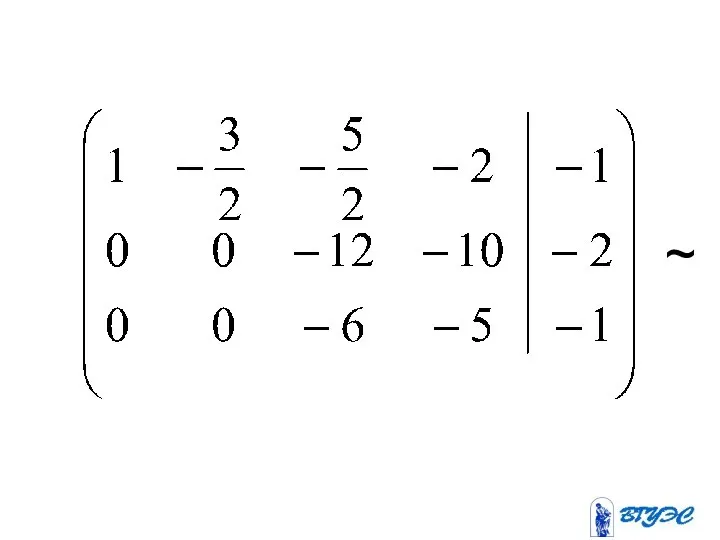
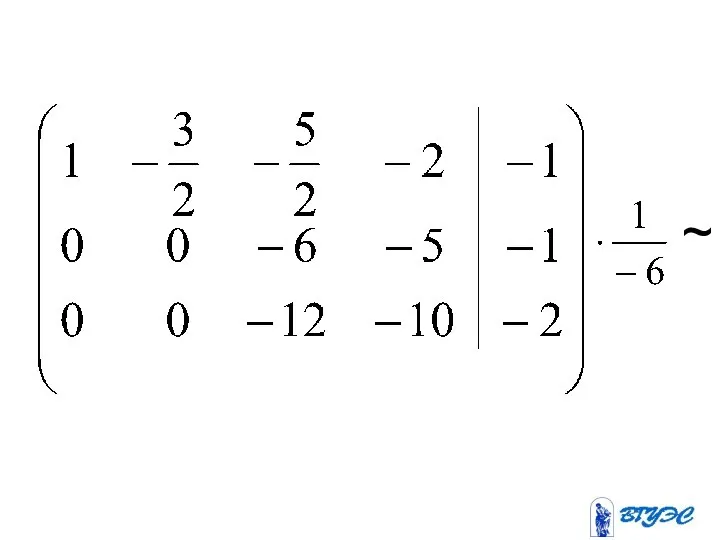
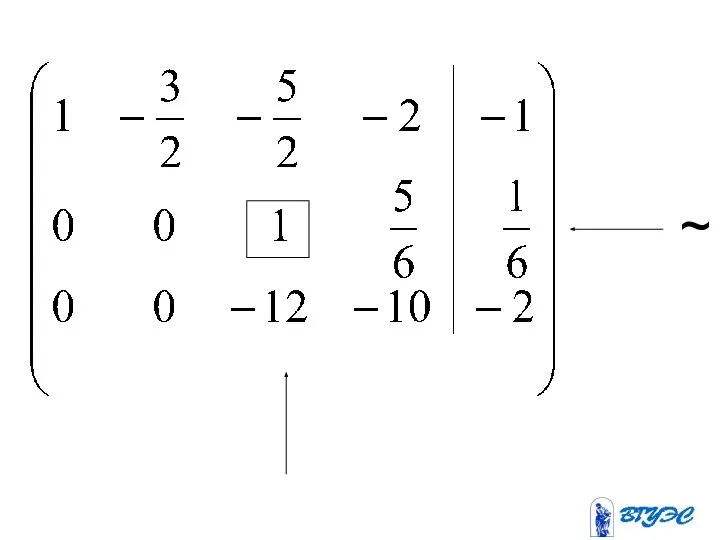
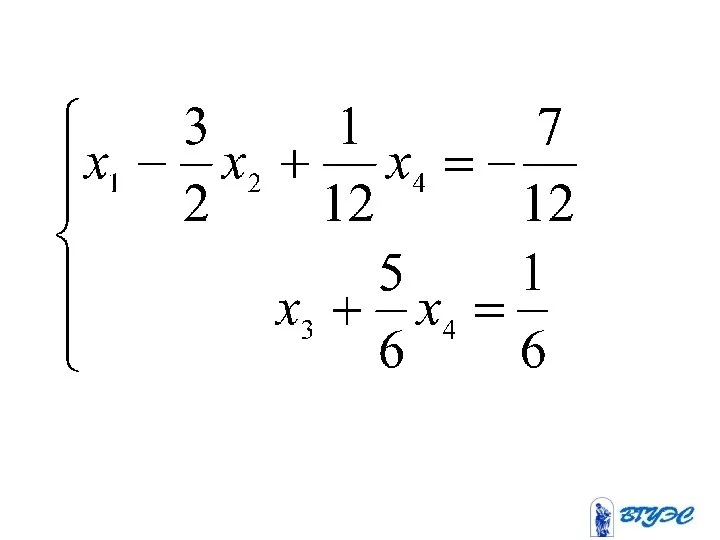
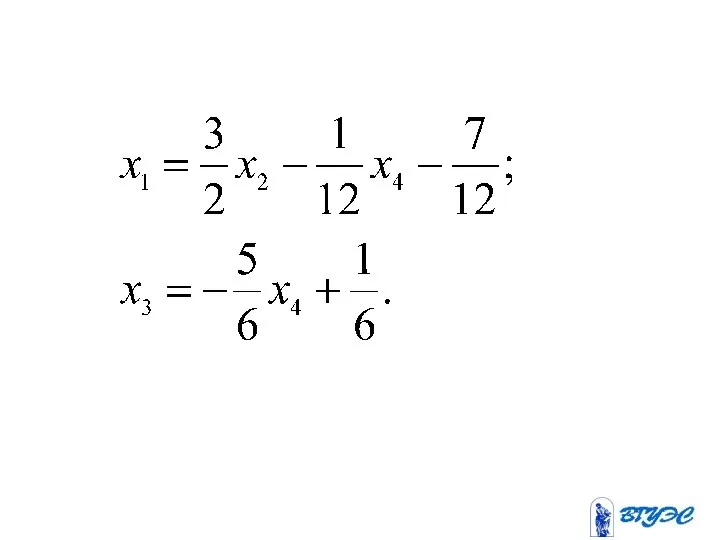
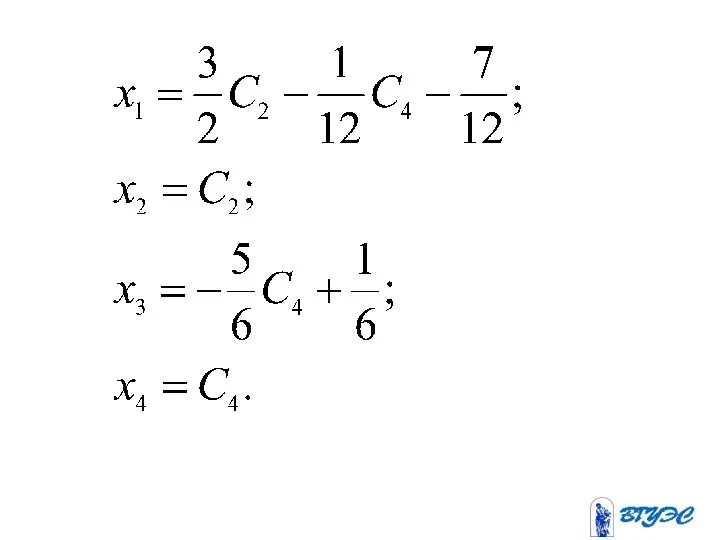


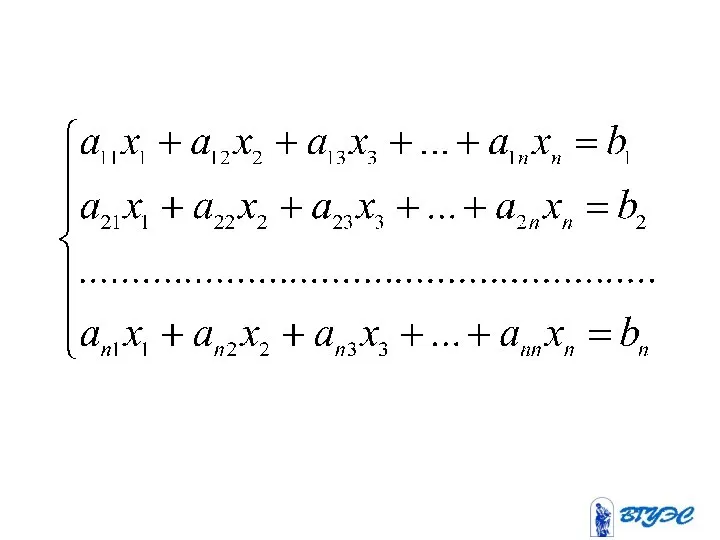


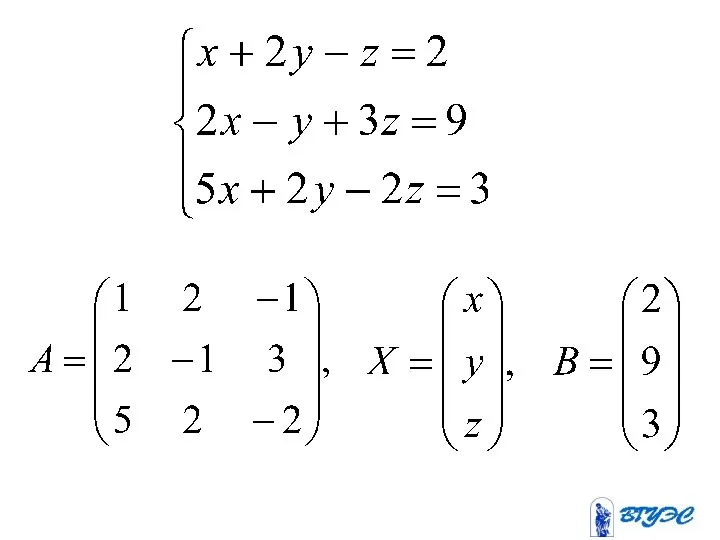
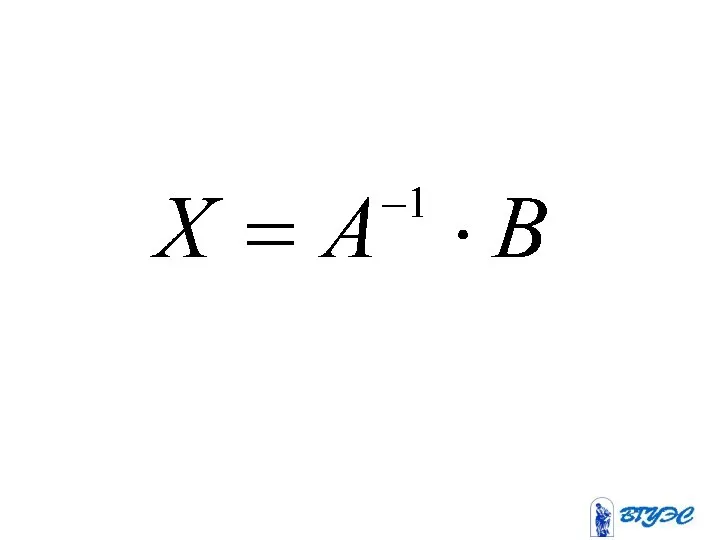
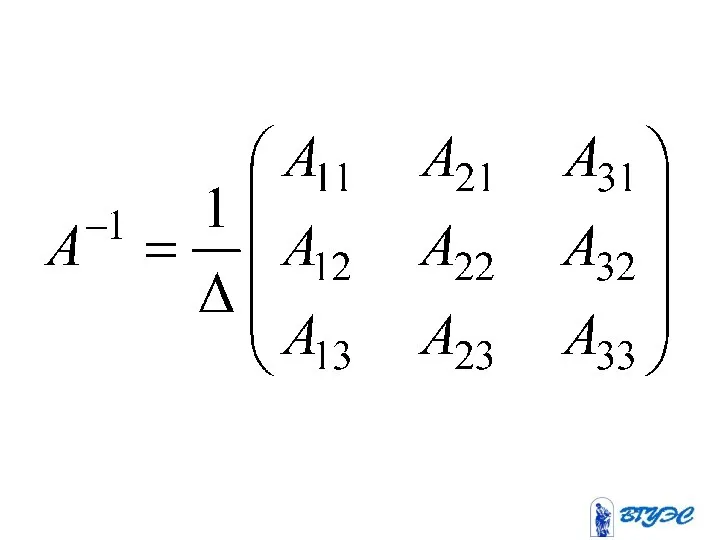
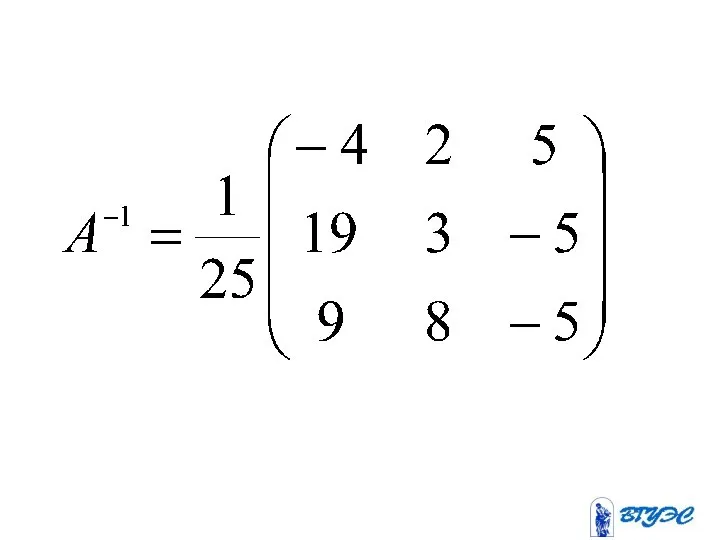
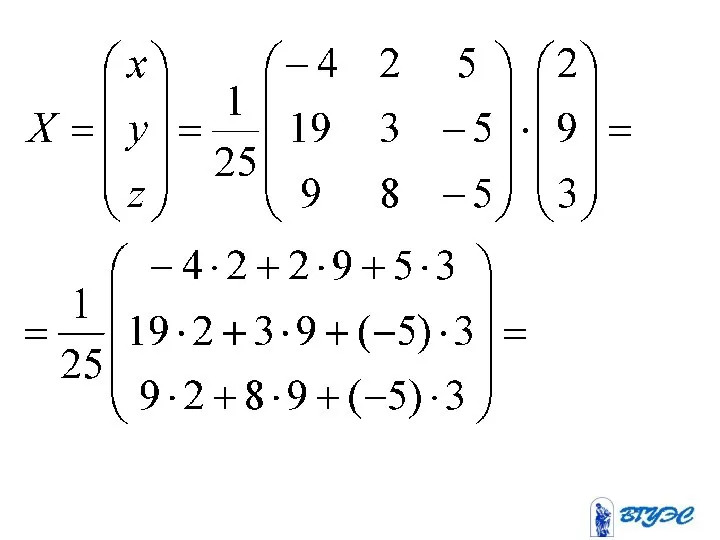
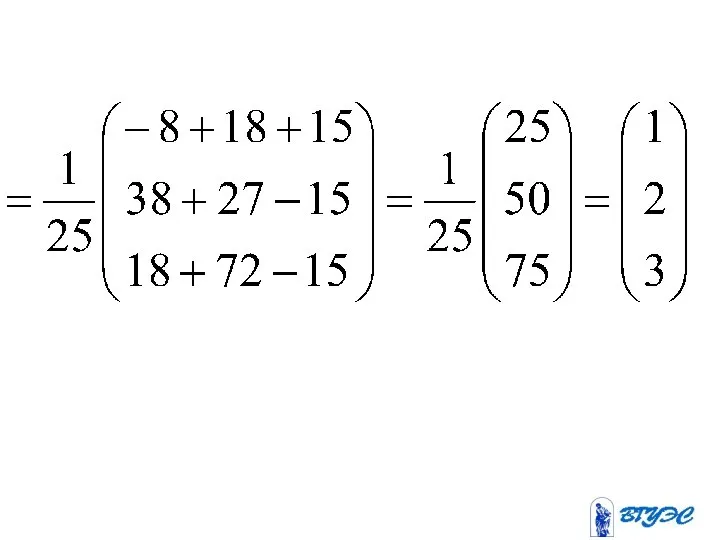
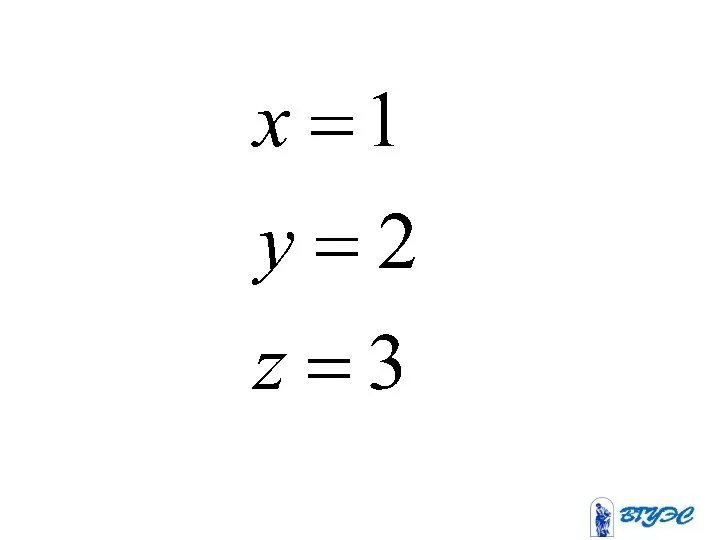


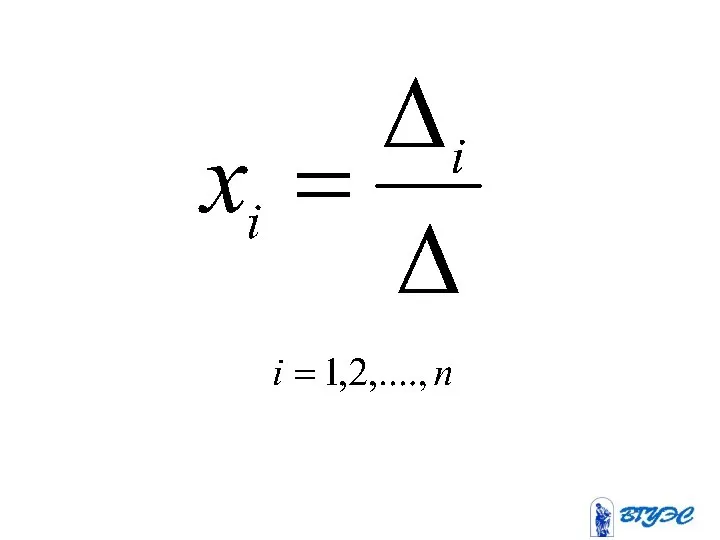


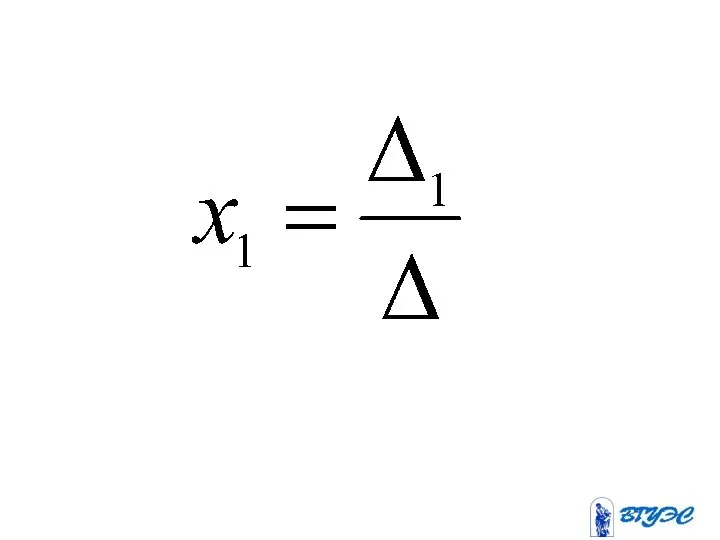
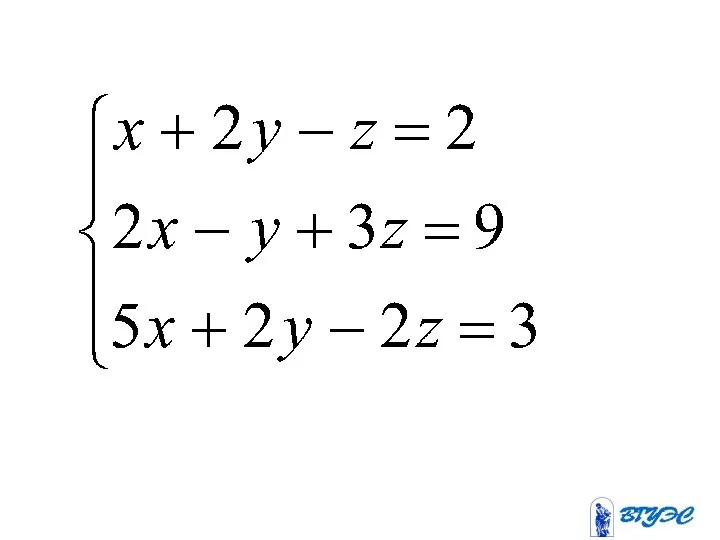
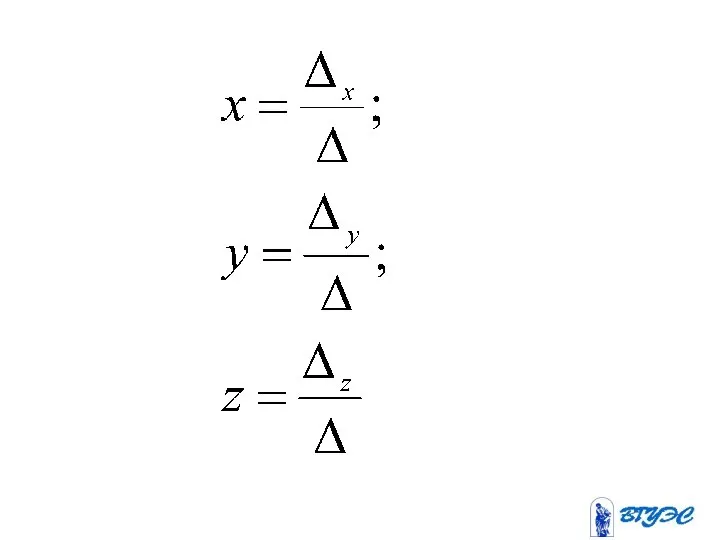
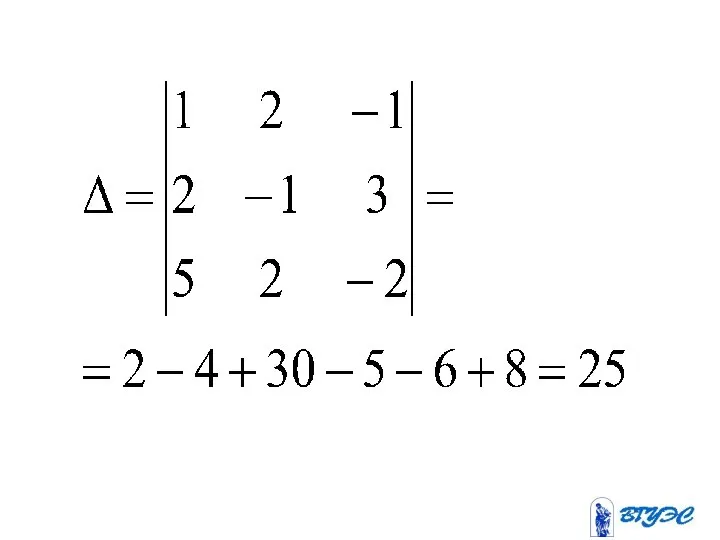
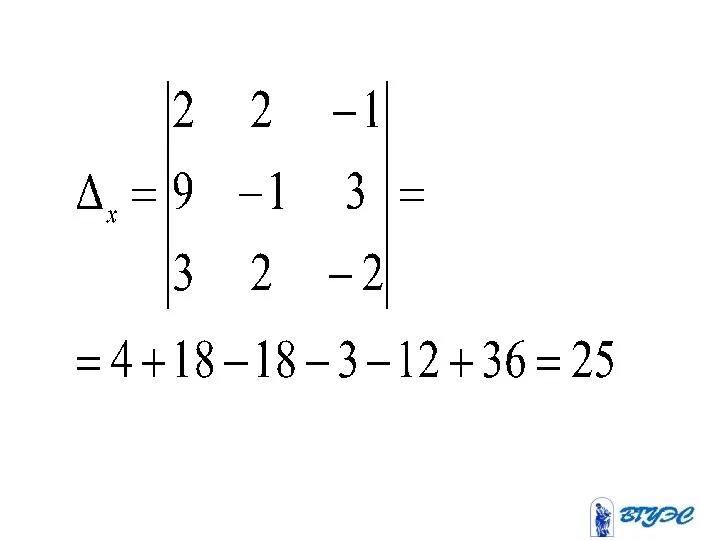
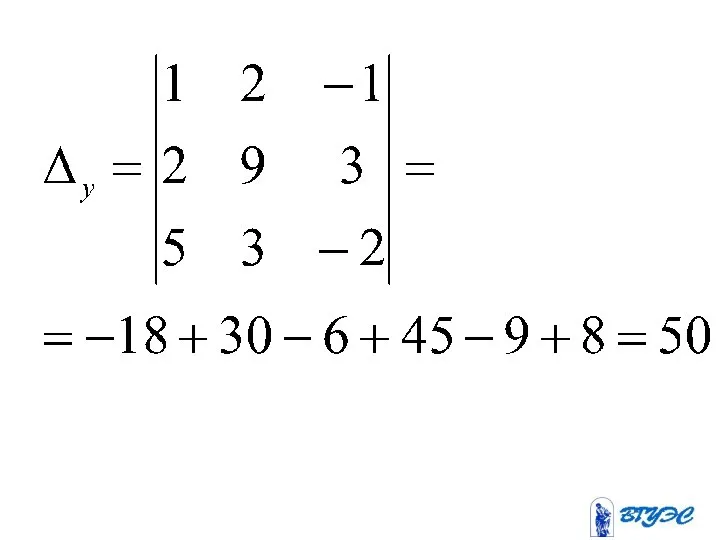
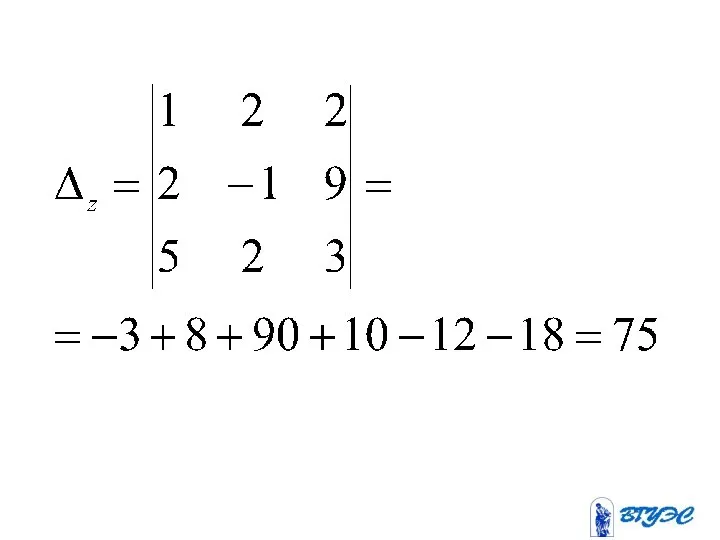
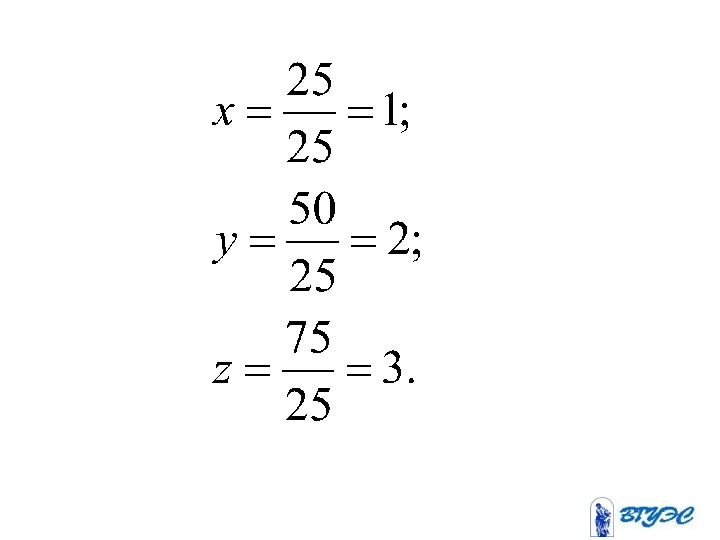

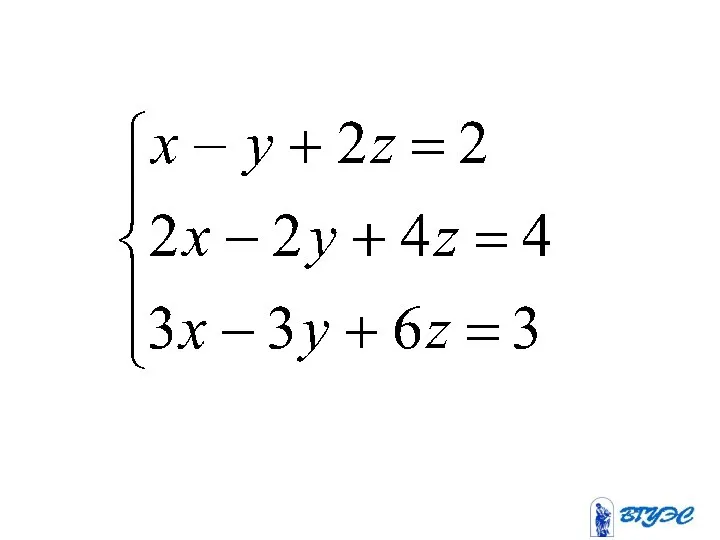
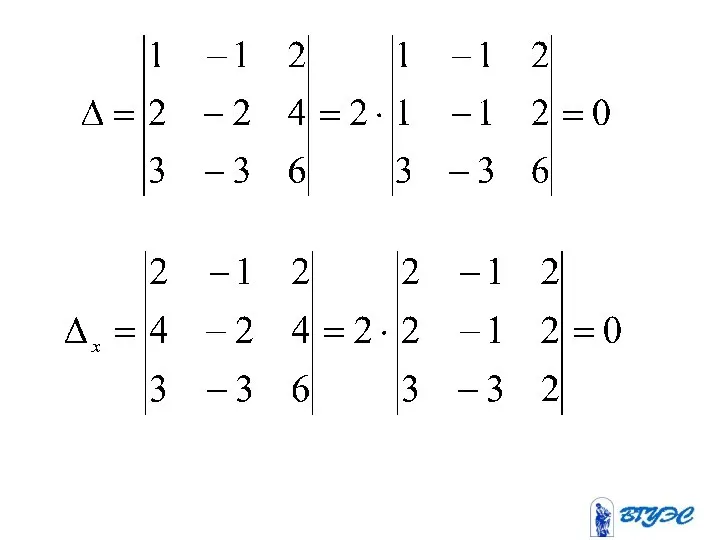
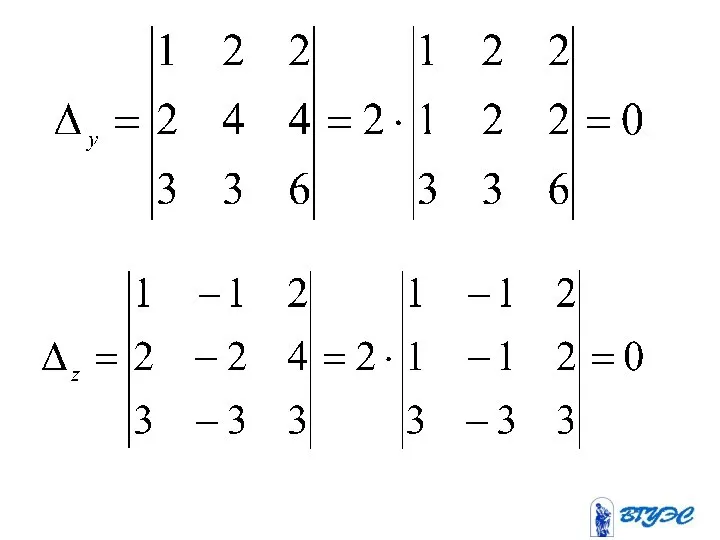

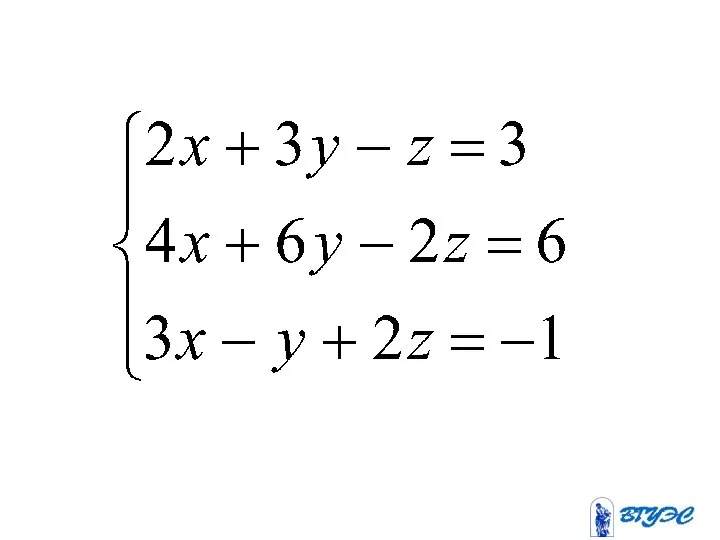
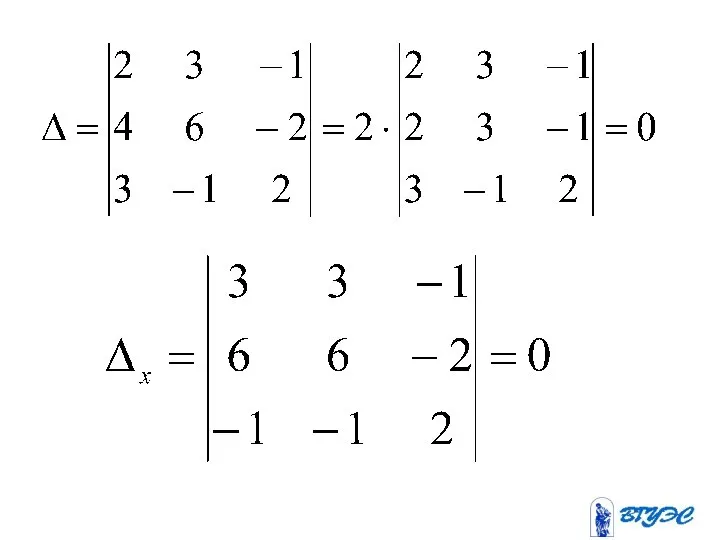


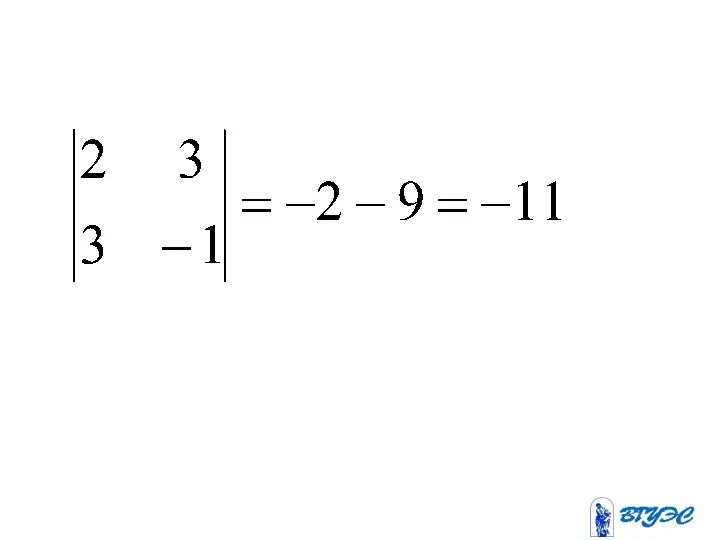
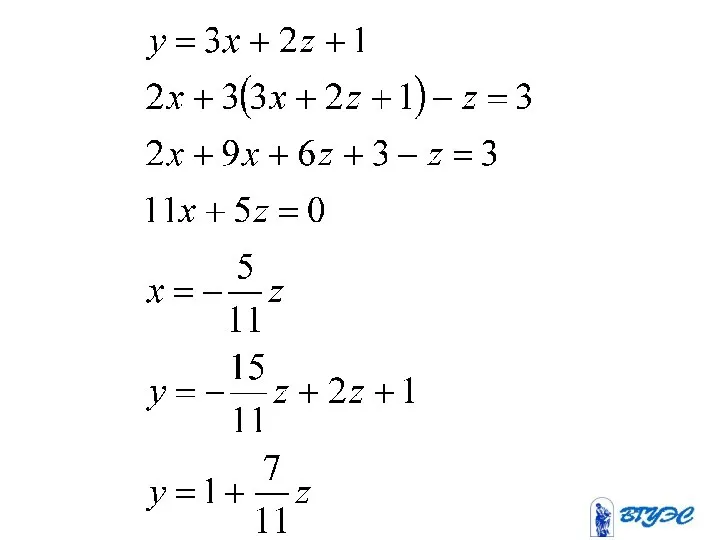
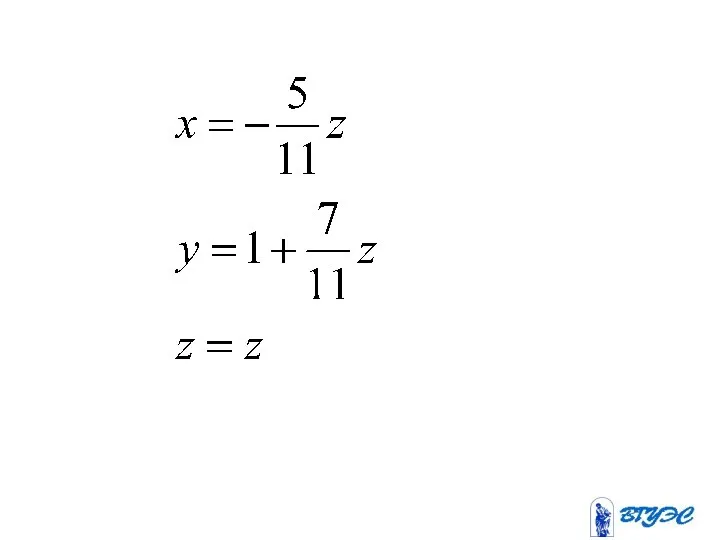


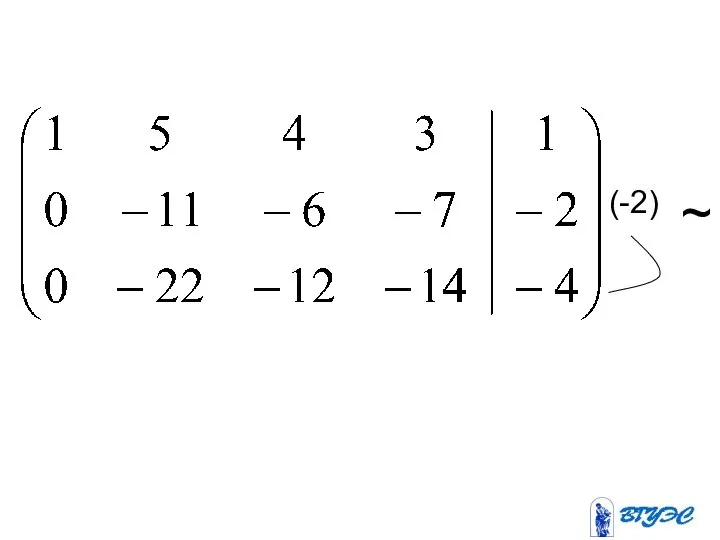



 О математике на разных языках
О математике на разных языках Осевая симметрия. 6 класс
Осевая симметрия. 6 класс Урок математики в 6 классе специальной (коррекционной) школы VIII вида по теме «Решение задач в 2-3 действия»
Урок математики в 6 классе специальной (коррекционной) школы VIII вида по теме «Решение задач в 2-3 действия»  Решение показательных уравнений и неравенств. 11 класс
Решение показательных уравнений и неравенств. 11 класс Дифференциал функции
Дифференциал функции Неопределенный интеграл Лекция7
Неопределенный интеграл Лекция7  Способи обчислення границь
Способи обчислення границь Задачи на готовых чертежах. Параллелограмм
Задачи на готовых чертежах. Параллелограмм Теорема Менелая и теорема Чевы в школьном курсе математики
Теорема Менелая и теорема Чевы в школьном курсе математики  Логарифмические уравнения и методы их решения
Логарифмические уравнения и методы их решения Статистические критерии различий (1)
Статистические критерии различий (1) Приемы и методы решения заданий С1 и С3
Приемы и методы решения заданий С1 и С3 Графический способ решения систем уравнений
Графический способ решения систем уравнений Квадратный трехчлен (часть 2)
Квадратный трехчлен (часть 2) Теорема Пифагора
Теорема Пифагора Баскакова Ирина Степеновна учитель математики МОУ «Томилинская СОШ №14»
Баскакова Ирина Степеновна учитель математики МОУ «Томилинская СОШ №14»  Деление и умножение положительных и отрицательных чисел. 6 класс
Деление и умножение положительных и отрицательных чисел. 6 класс Запись всех точек, соответствующих данным точкам единичной окружности
Запись всех точек, соответствующих данным точкам единичной окружности Сложение десятичных дробей Урок-игра 5класс Учитель Бойцова Т.И. МАОУСОШ д. Ореховно Мошенской район
Сложение десятичных дробей Урок-игра 5класс Учитель Бойцова Т.И. МАОУСОШ д. Ореховно Мошенской район  Второй признак подобия треугольников
Второй признак подобия треугольников «Математика в профессиях» Внеклассное мероприятие в 5 классе по математике Учитель: Ва
«Математика в профессиях» Внеклассное мероприятие в 5 классе по математике Учитель: Ва Введение в комбинаторику
Введение в комбинаторику Понятие производной. Дифференциал функции. Использование дифференциала в приближенных вычислениях
Понятие производной. Дифференциал функции. Использование дифференциала в приближенных вычислениях Системы линейных уравнений. (Тема 9.1)
Системы линейных уравнений. (Тема 9.1) График и свойства степенной функции
График и свойства степенной функции Элементы компьютерной математики. Клеточные автоматы. (Лекция 12)
Элементы компьютерной математики. Клеточные автоматы. (Лекция 12) Презентация по математике "Великие математики" - скачать бесплатно
Презентация по математике "Великие математики" - скачать бесплатно Вычисление производной и правила дифференцирования
Вычисление производной и правила дифференцирования