Содержание
- 2. n–мерной СВ или системой n случайных величин. Например, положение точки на плоскости определяется двумя числами –
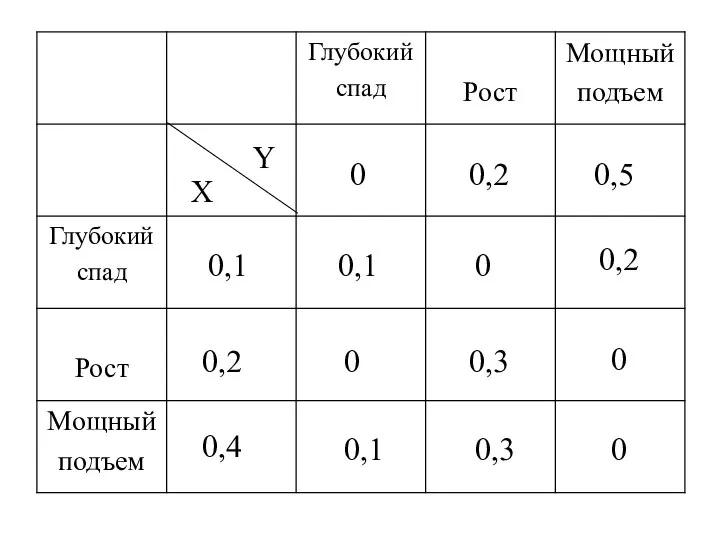
- 3. Тогда закон распределения системы двух случайных величин (X, Y) задается матрицей распределения, представленной в виде таблицы:
- 4. Здесь pij = P(X = xi, Y = yj). Так как все возможные комбинации { X
- 5. P(X = xi) = pi1+ pi2+ …+ pij + …+ pim = Σ pij – суммирование
- 6. Y X 0 0,2 0,5 0,1 0,2 0,4 0,1 0 0,2 0 0,3 0 0,1 0,3
- 7. Найти ЗР каждой СВ. х1=0,1: ЗР СВ Х: Х 0,1 0,2 0,4 Р 0,3 0,3 0,4
- 8. Числовые характеристики системы двух СВ Числовыми характеристиками системы двух СВ являются начальные и центральные моменты различных
- 9. Определение 2. Центральным моментом порядка k + s называется = Рассмотрим начальные и центральные моменты первого
- 10. Определение 3. Центральный момент называется ковариацией или корреляционным моментом и вычисляется по формуле:
- 11. Свойства ковариации 1) cov (X, X) = M((X – M(X))(X – M(X))) = = M(X –
- 12. Если то СВ X и Y коррелированны, т. е. связаны корреляционной зависимостью. Если же то СВ
- 13. Вернемся к примеру о портфеле акций и дадим экономический смысл начальным и центральным моментам первого и
- 14. D(X) или – степень разброса норм прибыли первого типа акций, следовательно, степень риска инвестиционного проекта Х.
- 15. риск разориться. Если cov (X, Y) одни акции идут вверх, а другие вниз, или, наоборот, следовательно,
- 16. коэффициент корреляции . М(Х) = 0,1*0,3 + 0,2*0,3 + 0,4*0,4 = 0,25; M(Y) = 0*0,2 +
- 17. = 0.1*0*0.1+ 0.1*0.2*0 + 0.1*0.5*0.2 + 0.2*0*0 + + 0.2*0.2*0.3 + 0.2*0.5*0 + 0.4*0*0.1 + 0.4*0.2*0.3
- 18. Определение. Условным законом распределения одной из СВ, входящих в систему (X,Y), называ- ется ЗР СВ Y
- 19. Например, Найдем условные законы распределения и условные математические ожидания.
- 20. При Х = Тогда условный закон распределения СВ Y при будет: Y 0 0,2 0,5 Математическое
- 21. При Y 0 0,2 0,5
- 22. При Y 0 0,2 0,5
- 23. При X 0,1 0,2 0,4 M(X/Y=0) = и т. д.
- 24. Определение. Случайные величины Х и Y, образующие систему, называются независимыми, если З.Р. одной из них не
- 26. Скачать презентацию




















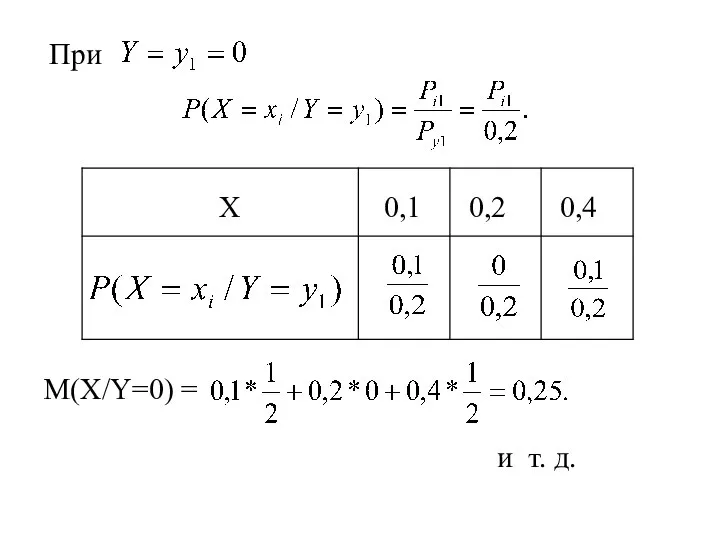

 Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Презентация по математике "Контроль процессов: Контроль качества количественных исследований" - скачать бесплатно
Презентация по математике "Контроль процессов: Контроль качества количественных исследований" - скачать бесплатно Решение задач по теории вероятностей. Подготовка к ГИА. (9 класс)
Решение задач по теории вероятностей. Подготовка к ГИА. (9 класс) Элементы конуса
Элементы конуса Соотношения между сторонами и углами в прямоугольном треугольнике
Соотношения между сторонами и углами в прямоугольном треугольнике Исследование функции
Исследование функции Интерактивный плакат: "Многогранники"
Интерактивный плакат: "Многогранники" Комсомольск - 2009
Комсомольск - 2009  Начертательная геометрия. Введение
Начертательная геометрия. Введение Операции над векторами
Операции над векторами Математика в архитектуре
Математика в архитектуре Метод растянутых координат. (Лекция 9)
Метод растянутых координат. (Лекция 9) Пересекающиеся прямые
Пересекающиеся прямые Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Презентация по математике "Задачи на построение сечений" - скачать
Презентация по математике "Задачи на построение сечений" - скачать  Возможные варианты внутренней структуры треугольника
Возможные варианты внутренней структуры треугольника Виды многогранников
Виды многогранников В царстве формул сокращенного умножения
В царстве формул сокращенного умножения Письменное умножение двух чисел, оканчивающихся нулями
Письменное умножение двух чисел, оканчивающихся нулями Устные приёмы умножения и деления чисел в концентре 1000
Устные приёмы умножения и деления чисел в концентре 1000 Признаки равенства треугольников
Признаки равенства треугольников Аттестационная работа. Разработка элективного курса «За страницами учебника математики»
Аттестационная работа. Разработка элективного курса «За страницами учебника математики» алгебра 8 класс 31.03.2020 Пересечение и объединение множеств
алгебра 8 класс 31.03.2020 Пересечение и объединение множеств Подготовила: Груздева Елена Викторовна, учитель математики МОУ СОШ №1 г. Шебекино
Подготовила: Груздева Елена Викторовна, учитель математики МОУ СОШ №1 г. Шебекино Заседание клуба «Знатоков» Тема: Применение квадратных уравнений для решения задач. Тип урока: Повторение и обобщение знаний.
Заседание клуба «Знатоков» Тема: Применение квадратных уравнений для решения задач. Тип урока: Повторение и обобщение знаний.  The use of methods for common fractions
The use of methods for common fractions Неравенства. Обобщающий урок. Подготовка к ЕГЭ
Неравенства. Обобщающий урок. Подготовка к ЕГЭ Статистический анализ выборок. Числовые характеристики ряда
Статистический анализ выборок. Числовые характеристики ряда