Содержание
- 2. УЧЕБНЫЕ ВОПРОСЫ: 1. Многомерная случайная величина и закон ее распределения 2. Функция и плотность распределения двумерной
- 3. Литература 1. Кремер Н.Ш. «Теория вероятностей и математическая статистика». Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2012.
- 4. Многомерная случайная величина и закон ее распределения ПЕРВЫЙ ВОПРОС
- 5. Определение. Случайной называется величина, которая в результате испытания может принять то или иное значение из некоторой
- 7. Определение. Если результат испытания характеризуется не одной случайной величиной, а некоторой системой случайных величин Х1, Х2,
- 8. Геометрически двумерную (X, Y) и трехмерную (X, У, Z) случайные величины можно изобразить случайной точкой или
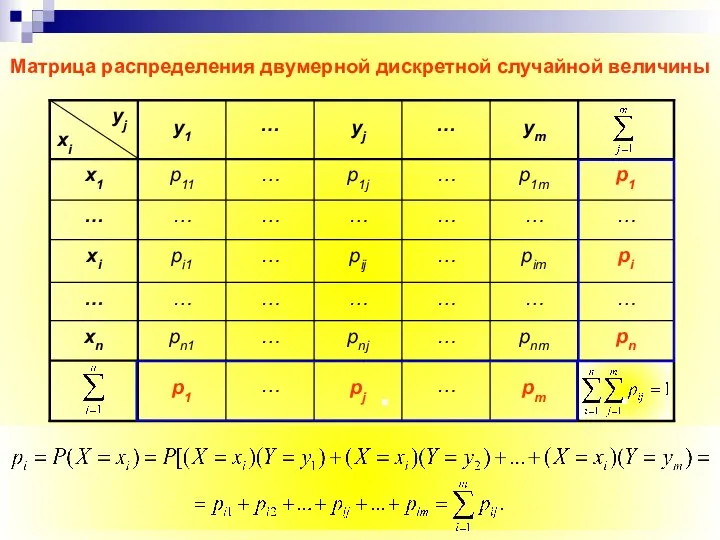
- 9. Матрица распределения двумерной дискретной случайной величины В каждой клетке (ij) матрицы располагаются вероятности произведе-ния событий рij
- 10. Таким образом, чтобы по таблице распределения найти вероятность того, что одномерная случайная величина примет определенное значение,
- 11. Определение. Если зафиксировать значение одного из аргументов, например, положить Y = уj то полученное распределение случайной
- 12. Пример. Закон распределения дискретной двумерной случайной вели-чины (X, Y) задан в таблице: Найти: а) законы распределения
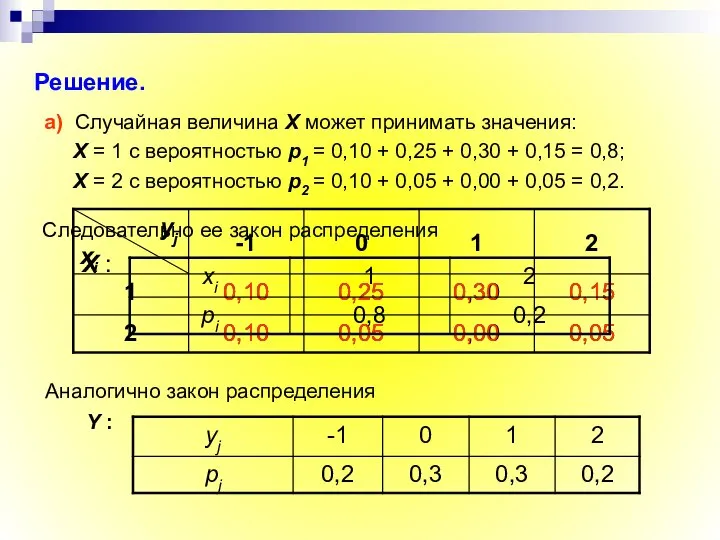
- 13. а) Случайная величина X может принимать значения: Х = 1 с вероятностью р1 = 0,10 +
- 14. б) Условный закон распределения X при условии, что Y = 2, получим, если вероятности рij, стоящие
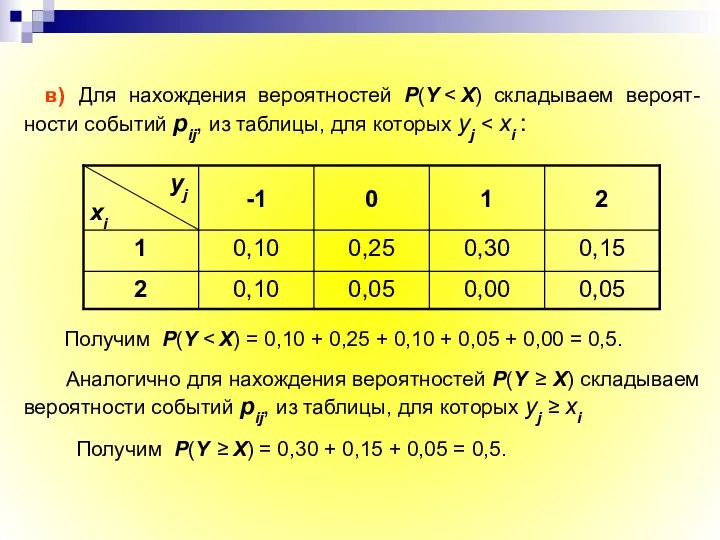
- 15. в) Для нахождения вероятностей P(Y Получим P(Y Аналогично для нахождения вероятностей P(Y ≥ X) складываем вероятности
- 16. Функция и плотность распределения двумерной случайной величины ВТОРОЙ ВОПРОС
- 17. Определение. Функцией распределения n - мерной случайной величины (Х1, Х2, ..., Хn) называется функция F (x1,
- 18. В нашей лекции мы в основном будем вести изложение для двумерной (n = 2) случайной величины;
- 19. СВОЙСТВА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ДВУМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 1. Функция распределения F(х,у) есть неотрицательная функция, заключенная между нулем
- 20. 4. Если один из аргументов обращается в +∞, функция рас-пределения F (х, у) становится равной функции
- 23. СВОЙСТВА ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ДВУМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 1. Плотность вероятности двумерной случайной величины есть неотрицательная функция, т.е.
- 24. Зная плотность вероятности двумерной случайной ве-личины (X,Y), можно найти функции распределения ее одно-мерных составляющих Х и
- 25. Пример. Двумерная случайная величина распределена равномерно в круге радиуса R = 1. Определить: а) выражение совместной
- 26. Определение. Условным законом распределения одной из одномерных сос-тавляющих двумерной случайной величины (X,Y) называется ее закон распределения,
- 27. Дифференцируя дважды данное равенство по аргументам х и у, получим f (x,y) = f1 (х)·f2 (у),
- 28. Числовые характеристики двумерной случайной величины ТРЕТИЙ ВОПРОС
- 29. При изучении двумерных случайных величин рассматриваются числовые характеристики одномерных составляющих X и Y — математические ожидания
- 30. Однако математические ожидания и дисперсии случайных величин X и Y недостаточно полно характеризуют двумерную случайную величину
- 31. СВОЙСТВА КОВАРИАЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН 1. Ковариация двух независимых случайных величин равна нулю. 2. Ковариация двух случайных
- 32. Определение. Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратических отклонений этих
- 33. НЕКОТОРЫЕ СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ 1. Математическое ожидание произведения двух случайных величин равно сумме произведения
- 34. Наряду с вышеуказанными рассматриваются такие числовые харак-теристики условных распределений, как: условные математические ожидания Mx( Y )
- 36. Скачать презентацию






























 Нахождение числа по заданному значению дроби
Нахождение числа по заданному значению дроби Үшбұрыштар теңдігінің белгілері
Үшбұрыштар теңдігінің белгілері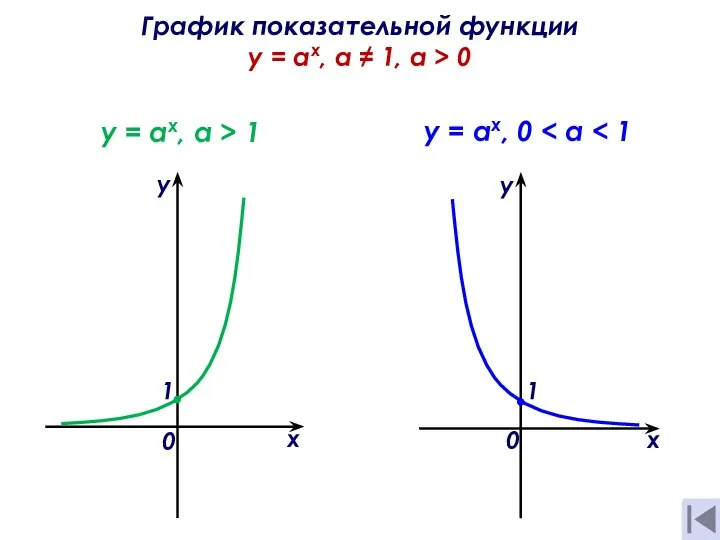 Показательные уравнения
Показательные уравнения Презентация по математике "Сложение натуральных чисел и его свойства." - скачать бесплатно_
Презентация по математике "Сложение натуральных чисел и его свойства." - скачать бесплатно_ Строительство бакалавриата. Приложения производной
Строительство бакалавриата. Приложения производной Тәуелсіз екі (және одан көп) популяциялардың орта мәндерін салыстыру
Тәуелсіз екі (және одан көп) популяциялардың орта мәндерін салыстыру Нелинейная парная регрессия
Нелинейная парная регрессия Метрологическая экспертиза
Метрологическая экспертиза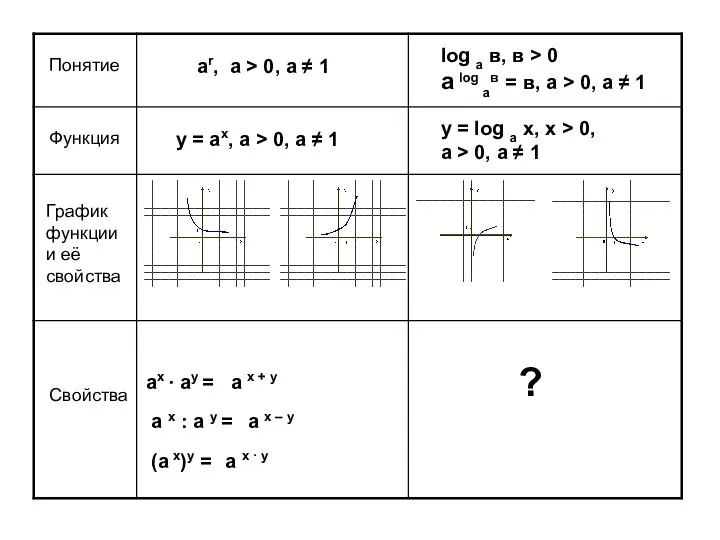 Свойства логарифмов
Свойства логарифмов ԱՎԱՐՏԱԿԱՆ ԱՇԽԱՏԱՆՔ
ԱՎԱՐՏԱԿԱՆ ԱՇԽԱՏԱՆՔ Квадрат суммы и квадрат разности 7 класс Курсова
Квадрат суммы и квадрат разности 7 класс Курсова Измерение отрезков и углов
Измерение отрезков и углов Свойства прямоугольных треугольников
Свойства прямоугольных треугольников Магические квадраты
Магические квадраты Пропорция. 6 класс
Пропорция. 6 класс Решение задания №4 ГИА
Решение задания №4 ГИА Аттестационная работа. Площадь треугольника. Урок математики в 5 классе
Аттестационная работа. Площадь треугольника. Урок математики в 5 классе Урок математики УМК «Школа России» 4 класс
Урок математики УМК «Школа России» 4 класс Признак Вейерштрасса равномерной сходимости
Признак Вейерштрасса равномерной сходимости Адаптивные фильтры. Практическое применение (1)
Адаптивные фильтры. Практическое применение (1) Інформаційні технології аналізу систем
Інформаційні технології аналізу систем Презентация по математике Натуральные числа и шкалы.
Презентация по математике Натуральные числа и шкалы.  Арифметическая прогрессия
Арифметическая прогрессия Презентация на тему Решение текстовых задач
Презентация на тему Решение текстовых задач  Логические функции
Логические функции Презентация на тему Систематизация задач с процентами и способы их решения при подготовке к ЕГЭ
Презентация на тему Систематизация задач с процентами и способы их решения при подготовке к ЕГЭ Многомерный регрессионный анализ. Алгоритмов бейесовского оценивания. Теорема о многомерном условном распределении вероятносте
Многомерный регрессионный анализ. Алгоритмов бейесовского оценивания. Теорема о многомерном условном распределении вероятносте Движение - это жизнь
Движение - это жизнь