Содержание
- 2. 6. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ 6.1 Теоремы о дифференцируемых функциях 6.2 Исследование функции и построение её графика 6.3
- 3. 6. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ 6.3 Нахождение наибольшего и наименьшего значений функции 6.3.1 Нахождение наибольшего и наименьшего значений
- 4. 1) Найти производную первого порядка функции. 2) Найти критические точки 1-го рода, принадлежащие интервалу (a; b).
- 5. Пример Найти наибольшее и наименьшее значения функции на отрезке: а) [0; 6]; б) [-3; 3]. 6.3.1
- 6. Пример 6.3.1 НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ НА ОТРЕЗКЕ И НА ИНТЕРВАЛЕ
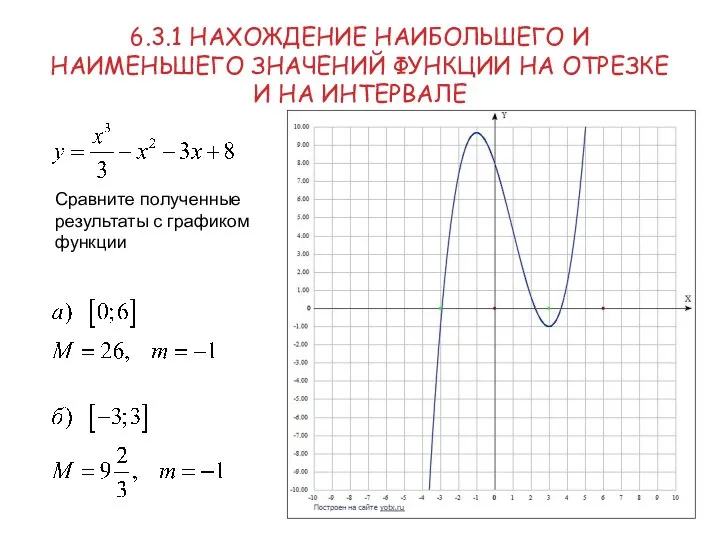
- 7. 6.3.1 НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ НА ОТРЕЗКЕ И НА ИНТЕРВАЛЕ Сравните полученные результаты с
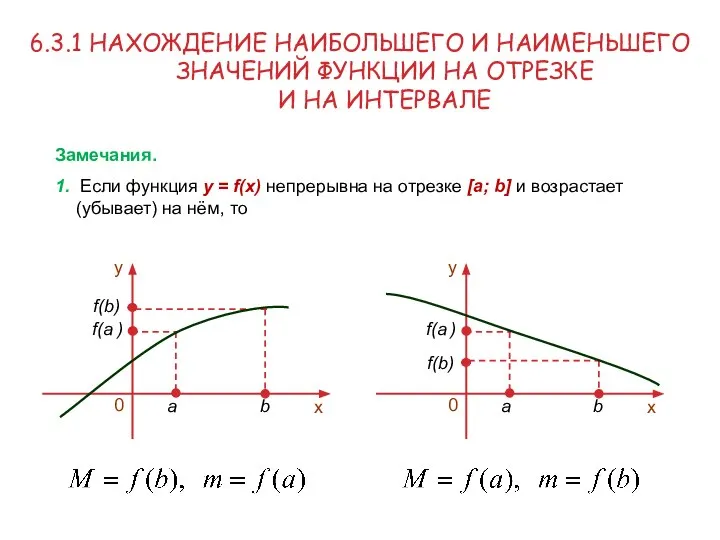
- 8. 6.3.1 НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ НА ОТРЕЗКЕ И НА ИНТЕРВАЛЕ Замечания. 1. Если функция
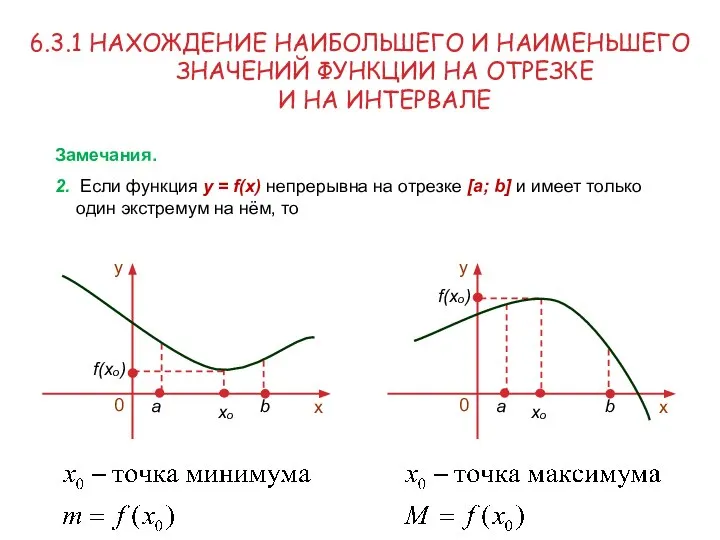
- 9. 6.3.1 НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ НА ОТРЕЗКЕ И НА ИНТЕРВАЛЕ Замечания. 2. Если функция
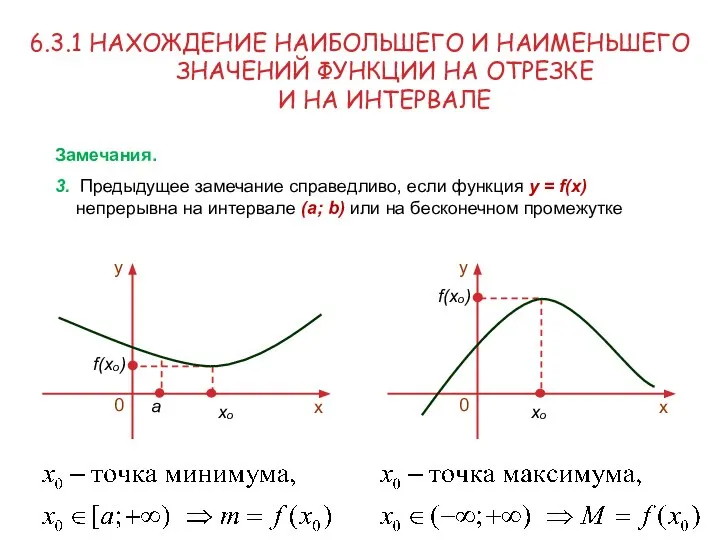
- 10. 6.3.1 НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ НА ОТРЕЗКЕ И НА ИНТЕРВАЛЕ Замечания. 3. Предыдущее замечание
- 11. 1. Убедиться, что заданный интервал принадлежит области определения D(f) функции у = f(x). 2. Найти производную
- 12. Нахождение наибольшего и наименьшего значений функции широко применяется при решении практических задач из различных дисциплин. Профессионально-ориентированные
- 13. 1) Этап построения модели. 1. Сформулировать задачу на математическом языке (математическая задача (1)). 2. Выявить в
- 14. 2) Этап решения. 6. Решить математическую задачу (2), используя соответствующие алгоритмы. 7. Решить математическую задачу (1),
- 15. Требуется оптимизировать затраты на постройку выставочного павильона объемом 1000 м3. Павильон должен иметь форму прямоугольного параллелепипеда,
- 16. Математическая задача (1). Найти длину и ширину прямоугольного параллелепипеда при заданных условиях. 6.3.2 ЗАДАЧИ НА ОПТИМИЗАЦИЮ
- 17. Тогда стоимость сооружения всего павильона: Выразим величину y через x и известные величины (объём). 6.3.2 ЗАДАЧИ
- 18. Область определения: Производная первого порядка: Критические точки 1-го рода: 6.3.2 ЗАДАЧИ НА ОПТИМИЗАЦИЮ Решение 2) Этап
- 19. Докажем, что она является точкой минимума (1 способ). Производная второго порядка: Заметим, что поэтому Найденная критическая
- 20. Представим размеры павильона, общая стоимость сооружения которого наименьшая, с точностью до сантиметров. Длина павильона ширина павильона
- 21. 6.3.2 ЗАДАЧИ НА ОПТИМИЗАЦИЮ Решение 3) Этап интерпретации. Рассчитаем стоимость сооружения частей павильона в рублях:
- 22. Задачи на оптимизацию и метод математического моделирования для их решения более подробно описан в методичке: 6.3.2
- 24. Скачать презентацию

















 Определитель матрицы третьего порядка (Занятие 3)
Определитель матрицы третьего порядка (Занятие 3) Умножение и деление на 10 на 100
Умножение и деление на 10 на 100 Квадратные уравнения. Решение неполных квадратных уравнений
Квадратные уравнения. Решение неполных квадратных уравнений Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной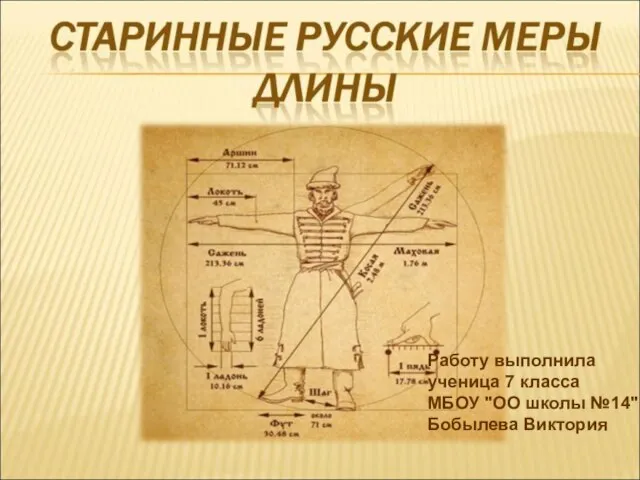 Система древнерусских мер длины
Система древнерусских мер длины Функции y = ax^2 + n и y = a(x – m)^2
Функции y = ax^2 + n и y = a(x – m)^2 Треугольник. 8 классе
Треугольник. 8 классе Степень с рациональным показателем
Степень с рациональным показателем Презентация урока математики 4 класс Учителя начальных классов МОУ лицей Павловой Светланы Аркадьевны
Презентация урока математики 4 класс Учителя начальных классов МОУ лицей Павловой Светланы Аркадьевны  Основные формулы к задачам типа В9
Основные формулы к задачам типа В9 Формула корней квадратного уравнения Левшина Мария Александровна учитель математики
Формула корней квадратного уравнения Левшина Мария Александровна учитель математики Тригонометрические уравнения
Тригонометрические уравнения Математика вокруг нас
Математика вокруг нас Задачи на построение
Задачи на построение Двуполостный гиперболоид
Двуполостный гиперболоид Свойства степени с натуральным показателем
Свойства степени с натуральным показателем ВИДЫ ДВИЖЕНИЯ
ВИДЫ ДВИЖЕНИЯ  Производная функции. Алгебра, 10 класс
Производная функции. Алгебра, 10 класс Жер эллипсоиды мен сфера туралы тұсінік
Жер эллипсоиды мен сфера туралы тұсінік Устный счет
Устный счет  Показательные уравнения и неравенства
Показательные уравнения и неравенства Космос
Космос Сложение чисел с разными знаками
Сложение чисел с разными знаками Нахождение дроби от числа
Нахождение дроби от числа ГИА 2011. Экзамен в новой форме математика. Тренировочный вариант экзаменационной работы государственной итоговой аттестации
ГИА 2011. Экзамен в новой форме математика. Тренировочный вариант экзаменационной работы государственной итоговой аттестации Первый признак равенства треугольников. Задачи для устной работы
Первый признак равенства треугольников. Задачи для устной работы МОУ СОШ №256 г.Фокино Приморский край. Каратанова Марина Николаевна.
МОУ СОШ №256 г.Фокино Приморский край. Каратанова Марина Николаевна.  Презентация по математике "Бизнес-игра" - скачать бесплатно
Презентация по математике "Бизнес-игра" - скачать бесплатно