Содержание
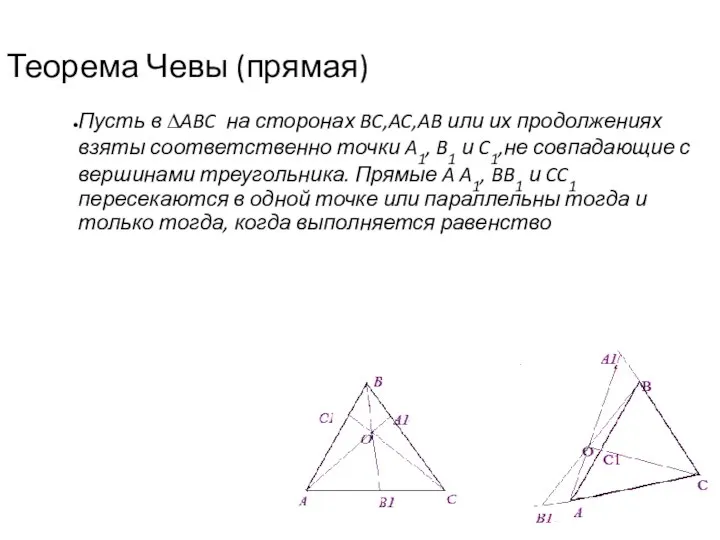
- 2. Теорема Чевы (прямая) Пусть в ∆ABC на сторонах BC,AC,AB или их продолжениях взяты соответственно точки A1,
- 3. Доказательство Предположим, что прямые АА1, ВВ1, СС1 пересекаются в точке О. Через вершину С треугольника ABC
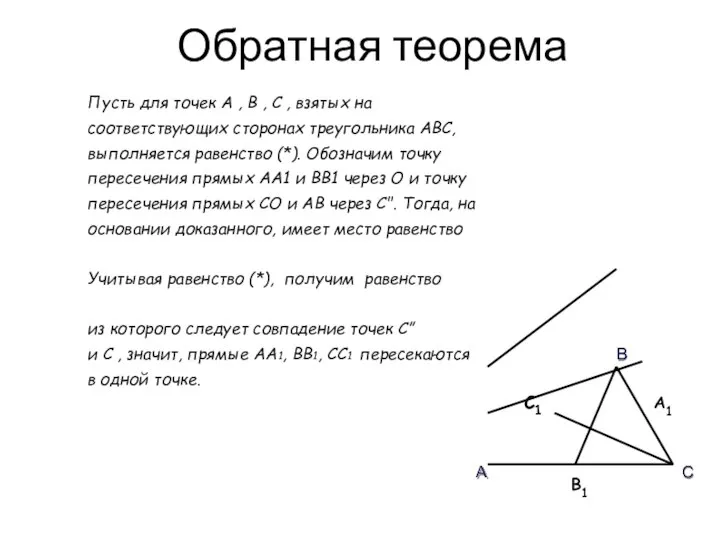
- 4. Обратная теорема Пусть для точек А , В , С , взятых на соответствующих сторонах треугольника
- 5. Следствия Теорема Чевы Следствие1. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении
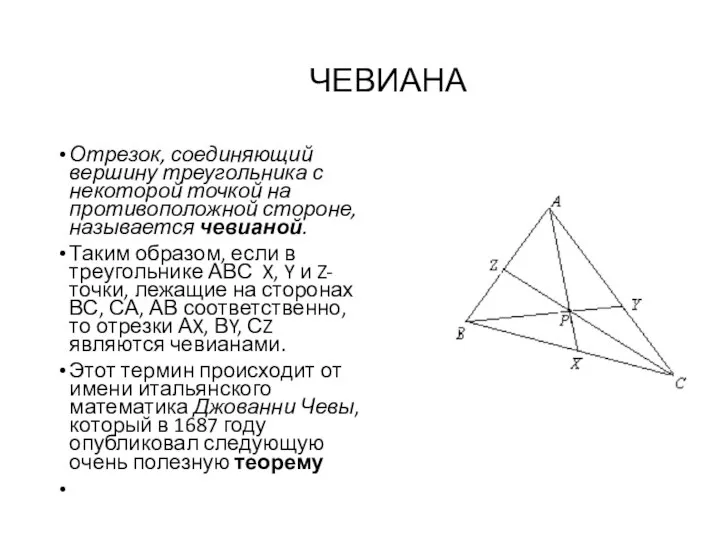
- 6. ЧЕВИАНА Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется чевианой. Таким образом, если
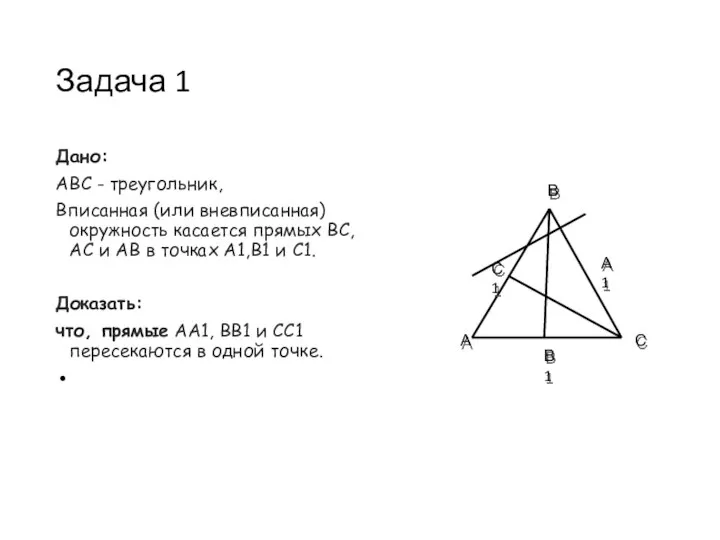
- 7. Задача 1 Дано: АВС - треугольник, Вписанная (или вневписанная) окружность касается прямых ВС, АС и АВ
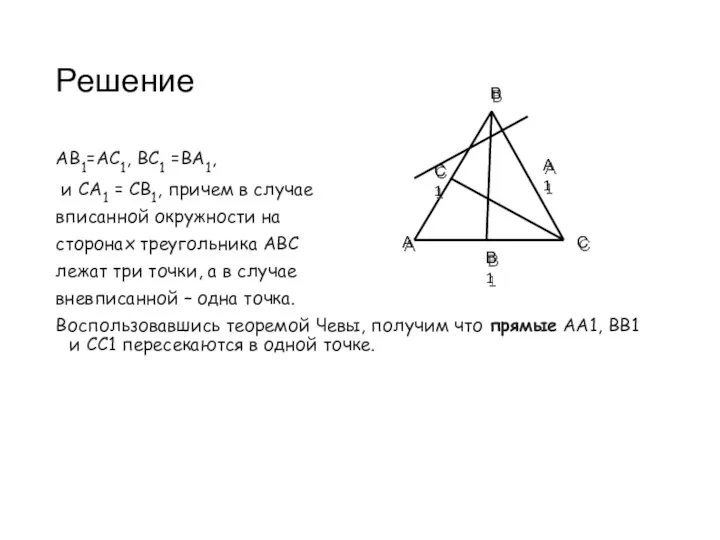
- 8. Решение АВ1=АС1, ВС1 =ВА1, и СА1 = СВ1, причем в случае вписанной окружности на сторонах треугольника
- 10. Скачать презентацию


 Скрещивающиеся прямые
Скрещивающиеся прямые Теорема умножения вероятностей. Решение задач В-10
Теорема умножения вероятностей. Решение задач В-10 Аттестационная работа. Решение задач повышенной сложности
Аттестационная работа. Решение задач повышенной сложности Упрощение выражений (2)
Упрощение выражений (2) Сравнение натуральных чисел
Сравнение натуральных чисел Множества. Логические символы. (Лекция 1)
Множества. Логические символы. (Лекция 1)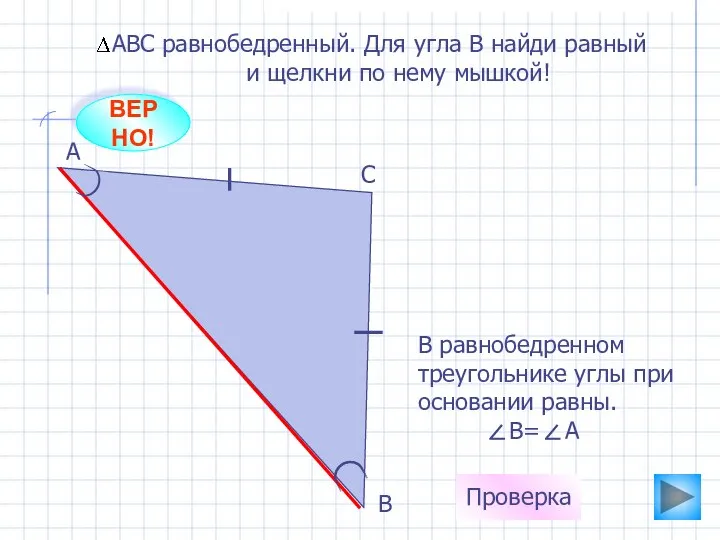 Равнобедренный треугольник. Решение задач
Равнобедренный треугольник. Решение задач Освоение основных универсальных предметных знаний и умений в курсе технологии
Освоение основных универсальных предметных знаний и умений в курсе технологии Выполнила: О.А.Трубкина
Выполнила: О.А.Трубкина  Презентация по математике "ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ ДЛЯ ДОШКОЛЬНИКОВ" - скачать
Презентация по математике "ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ ДЛЯ ДОШКОЛЬНИКОВ" - скачать  Формулы двойного аргумента
Формулы двойного аргумента Диаграмма и решение задач. Задачи на приведение к единице. 3 класс П Н Ш
Диаграмма и решение задач. Задачи на приведение к единице. 3 класс П Н Ш  Нормальные формы для формул алгебры высказываний
Нормальные формы для формул алгебры высказываний Триангуляция области
Триангуляция области Отношения и проценты
Отношения и проценты Отрезок и его длина
Отрезок и его длина Презентация по математике "Цифра 5" - скачать бесплатно
Презентация по математике "Цифра 5" - скачать бесплатно Элементарные функции
Элементарные функции Презентация по математике "Уравнения (нахождение делимого)" - скачать
Презентация по математике "Уравнения (нахождение делимого)" - скачать  Квадратные уравнения. Задачи
Квадратные уравнения. Задачи Решение задач с процентами. Я выбрала эту тему , потому что проценты изучаются как основные, типовые лишь в 5 – ом , 6 – ом классе, а з
Решение задач с процентами. Я выбрала эту тему , потому что проценты изучаются как основные, типовые лишь в 5 – ом , 6 – ом классе, а з Основное свойство дроби. Сокращение дроби
Основное свойство дроби. Сокращение дроби Системы нечеткого вывода
Системы нечеткого вывода Радианная мера угла. Вращательное движение
Радианная мера угла. Вращательное движение Презентация по математике "Интересная математика для 6 класса" - скачать бесплатно
Презентация по математике "Интересная математика для 6 класса" - скачать бесплатно Геометрия. Задача
Геометрия. Задача Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности Параллельные прямые
Параллельные прямые