Содержание
- 2. Определения и примеры Хотя обычно теорию графов считают одной из современных областей математики, ее начало датируется
- 3. Определения и примеры Эйлер (1707 – 1783) родился в Швейцарии и провел большую часть жизни в
- 4. Определения и примеры Как и большинство выдающихся математиков того времени, Эйлер внес вклад почти в каждую
- 5. Определения и примеры Что такое ‘граф’? Интуитивно, граф – это набор точек, называемых ‘вершинами’, и набор
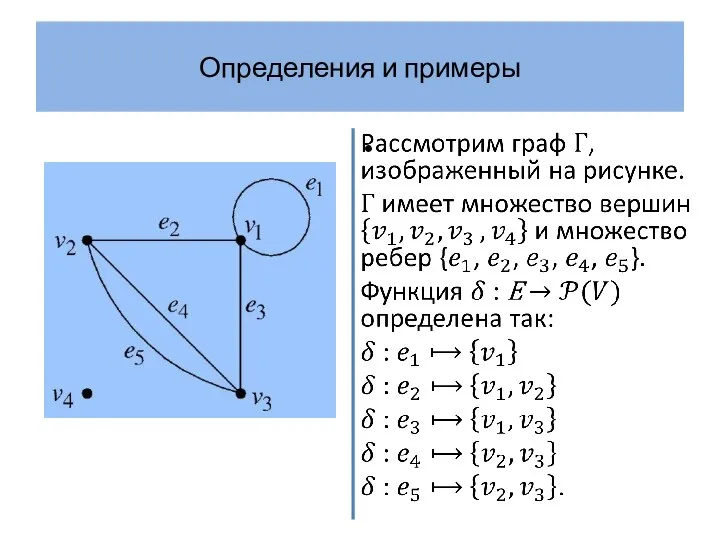
- 6. Определения и примеры
- 7. Определения и примеры
- 8. Определения и примеры
- 9. Определения и примеры
- 10. Определения и примеры
- 11. Определения и примеры
- 12. Определения и примеры Определение 2 Степенная последовательность графа – это последовательность степеней его вершин, записанных в
- 13. Определения и примеры
- 14. Определения и примеры
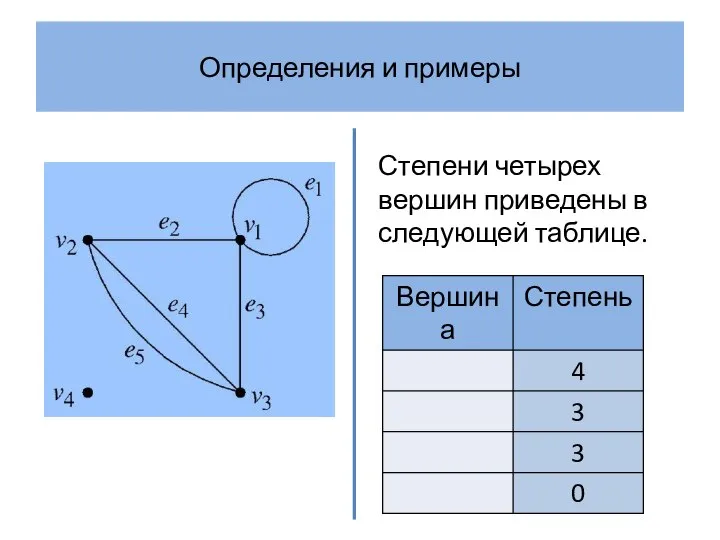
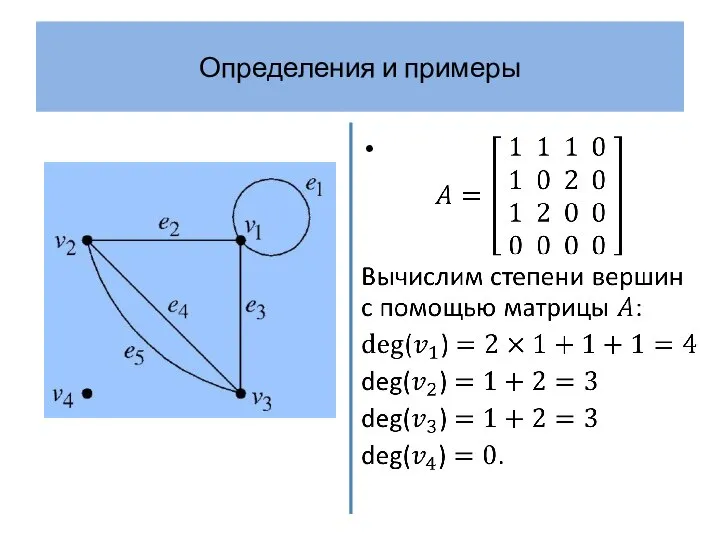
- 15. Определения и примеры Степени четырех вершин приведены в следующей таблице.
- 16. Определения и примеры
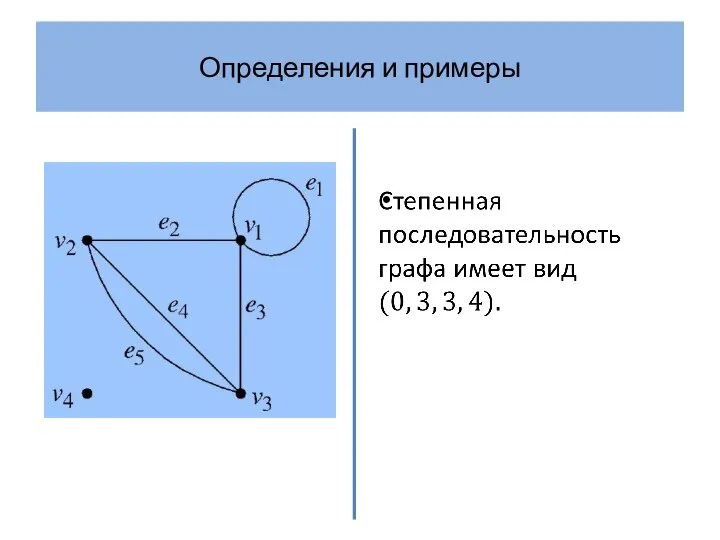
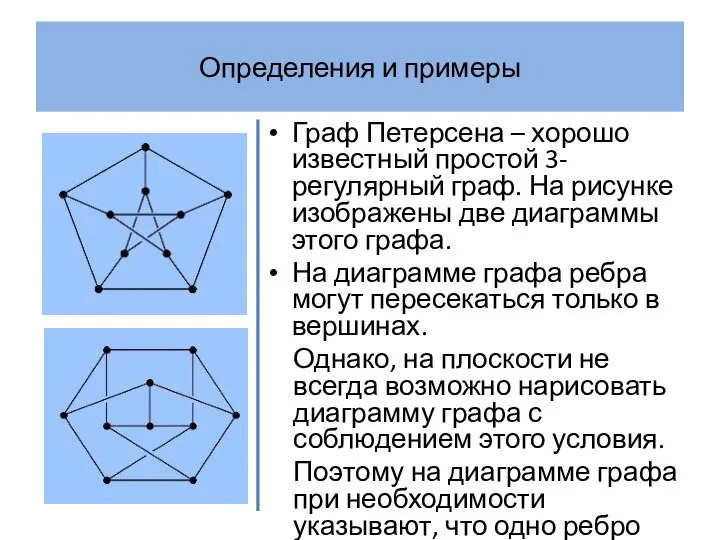
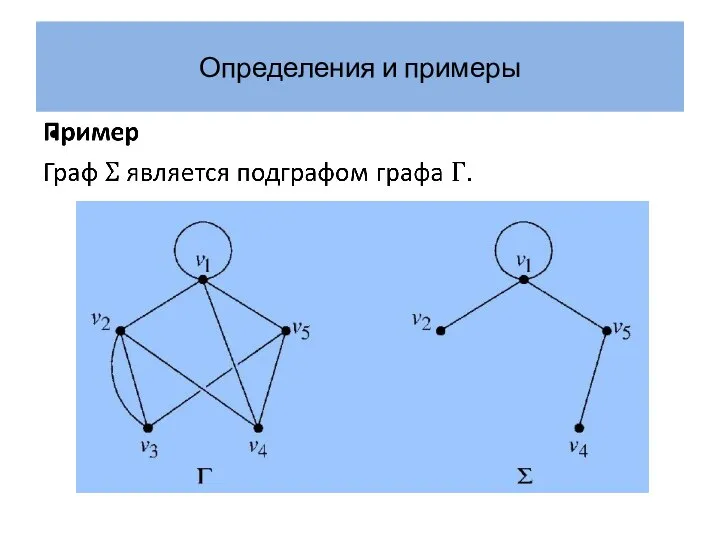
- 17. Определения и примеры Граф Петерсена – хорошо известный простой 3-регулярный граф. На рисунке изображены две диаграммы
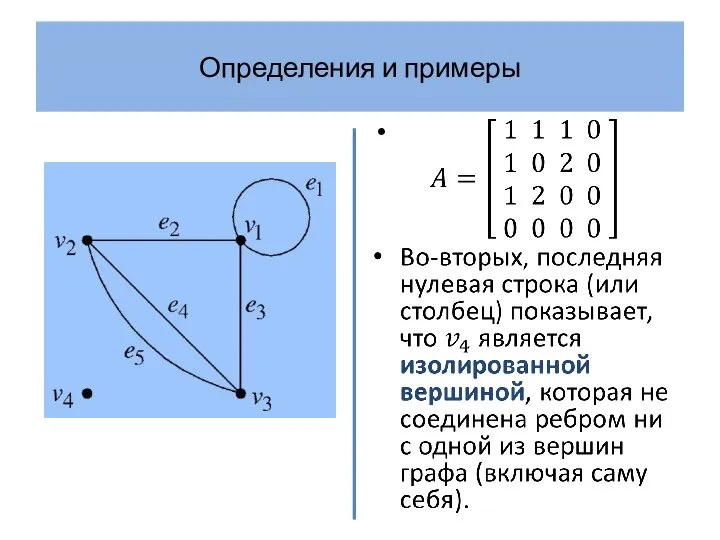
- 18. Определения и примеры Определение 3 Нулевым графом (или вполне несвязным графом) называется граф с пустым множеством
- 19. Определения и примеры
- 20. Определения и примеры Примеры Так как полный граф является простым, то в нем нет петель, и
- 21. Определения и примеры
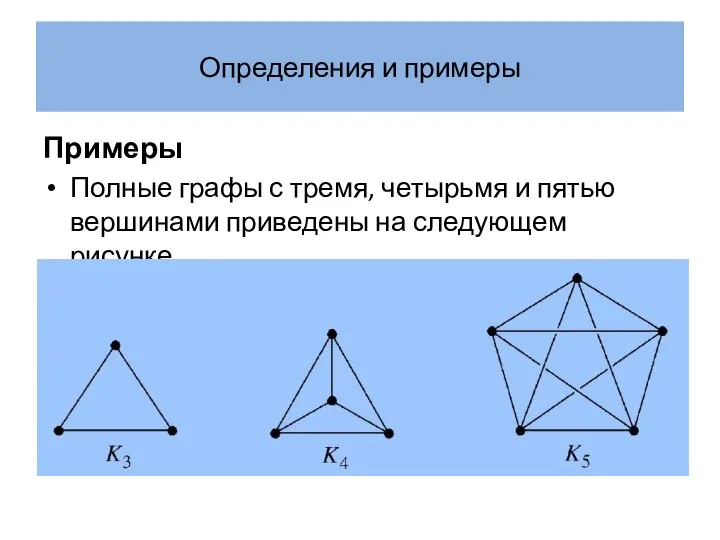
- 22. Определения и примеры Примеры Полные графы с тремя, четырьмя и пятью вершинами приведены на следующем рисунке.
- 23. Определения и примеры
- 24. Определения и примеры
- 25. Определения и примеры
- 26. Определения и примеры
- 27. Определения и примеры
- 28. Определения и примеры
- 29. Определения и примеры
- 30. Определения и примеры
- 31. Определения и примеры
- 32. Определения и примеры
- 33. Определения и примеры
- 34. Определения и примеры
- 35. Определения и примеры Примеры Матрица смежности полного графа – матрица с нулями на главной диагонали (так
- 36. Определения и примеры
- 37. Определения и примеры
- 38. Определения и примеры
- 39. Пути и циклы По аналогии с дорожной картой мы можем рассматривать различные типы ‘путешествий’ в графе.
- 40. Пути и циклы
- 41. Пути и циклы
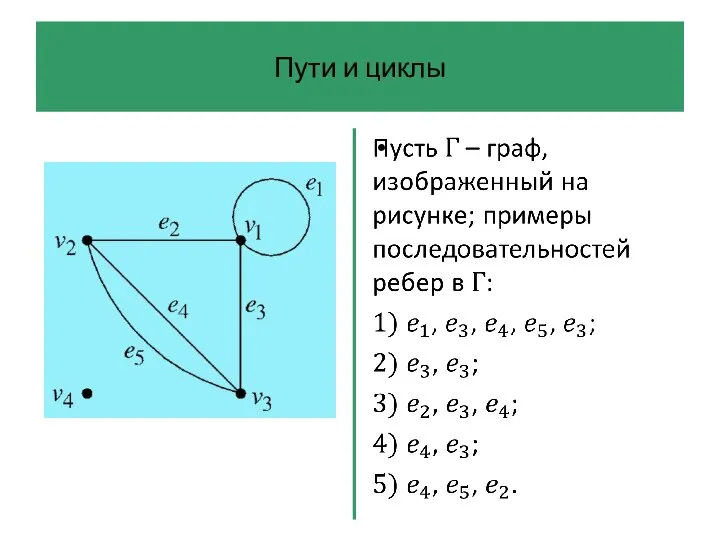
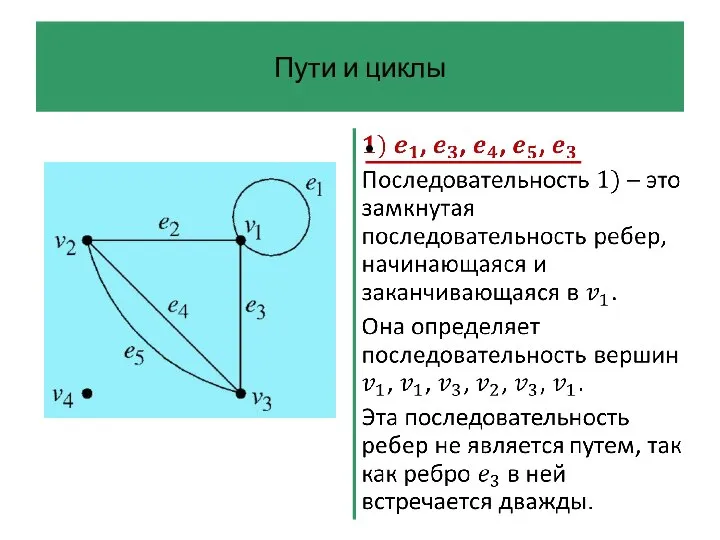
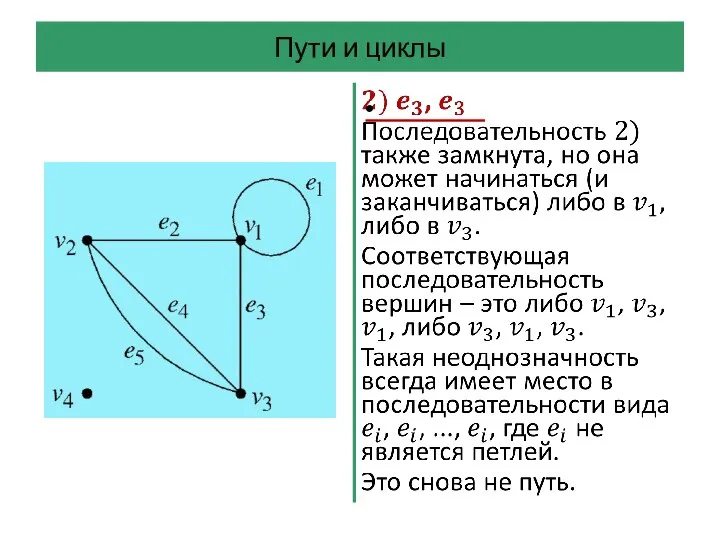
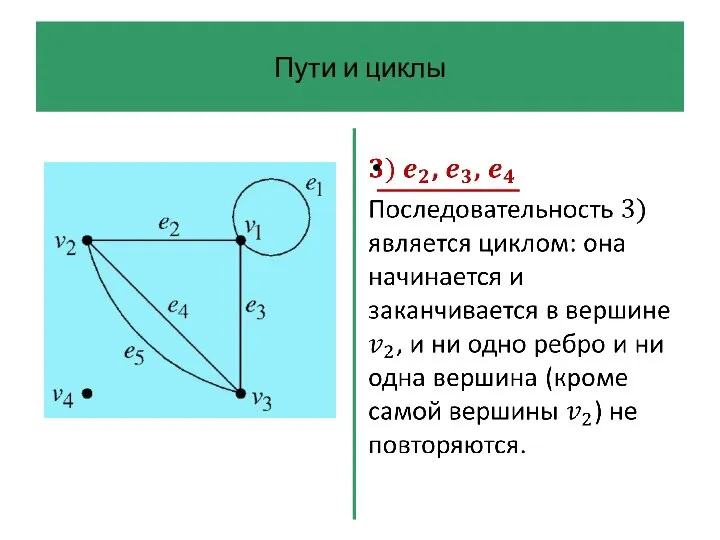
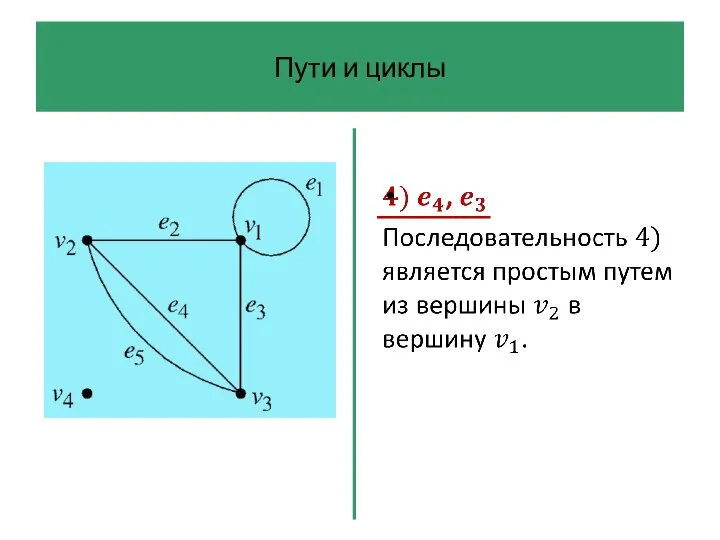
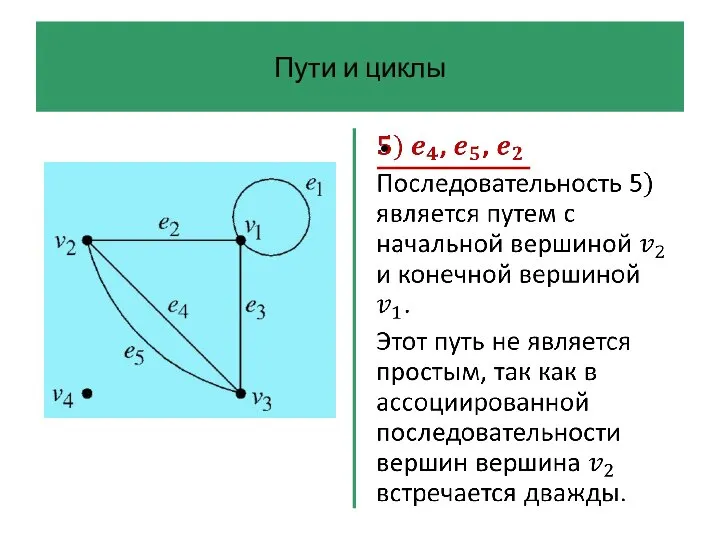
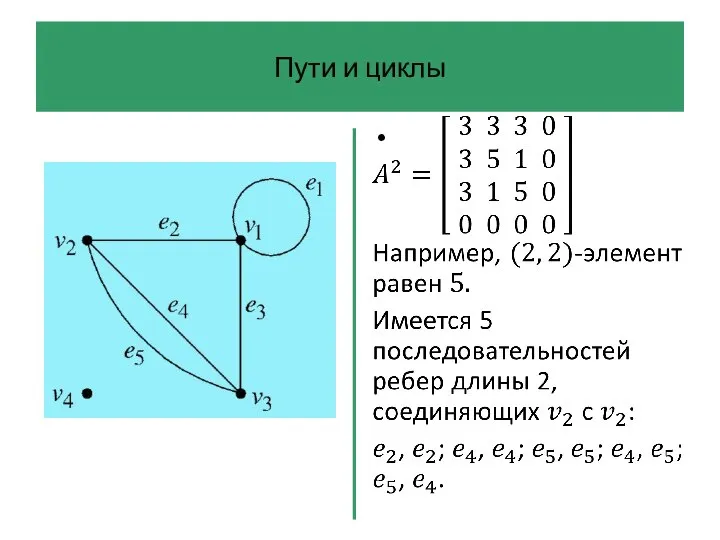
- 42. Пути и циклы Последовательность ребер графа – это произвольная последовательность ребер, которую можно начертить на диаграмме
- 43. Пути и циклы
- 44. Пути и циклы
- 45. Пути и циклы
- 46. Пути и циклы
- 47. Пути и циклы
- 48. Пути и циклы
- 49. Пути и циклы
- 50. Пути и циклы
- 51. Пути и циклы
- 52. Пути и циклы
- 54. Пути и циклы
- 55. Пути и циклы
- 56. Пути и циклы
- 57. Пути и циклы
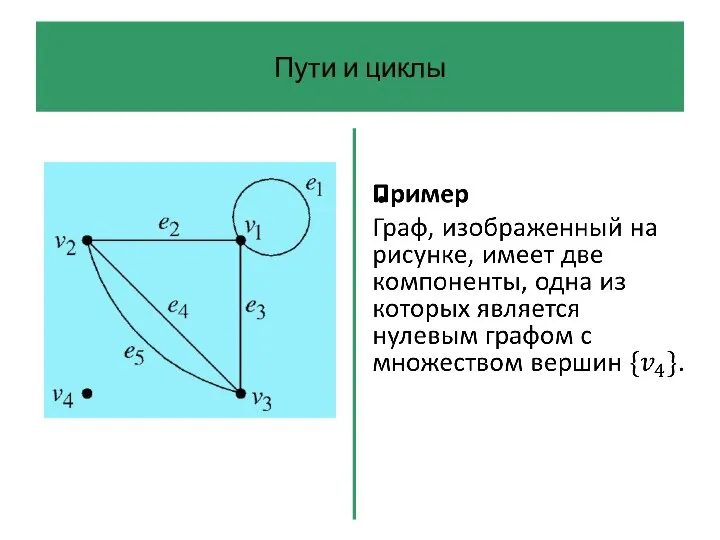
- 58. Пути и циклы На интуитивном уровне ясно, что некоторые графы являются ‘единым целым’, а другие состоят
- 59. Пути и циклы Определение 7 Граф называется связным, если для любых двух его различных вершин существует
- 60. Пути и циклы
- 61. Пути и циклы Компоненты графа – это его связные ‘куски’. В частности, связный граф имеет только
- 62. Пути и циклы
- 63. Пути и циклы
- 64. Пути и циклы
- 65. Пути и циклы
- 66. Пути и циклы
- 68. Скачать презентацию




































 Linear Regression Models. Week 7
Linear Regression Models. Week 7 Алгебра высказываний при решении логических задач. Дизъюнктивные нормальные формы Лекция 3
Алгебра высказываний при решении логических задач. Дизъюнктивные нормальные формы Лекция 3 Методы исследования математических моделей
Методы исследования математических моделей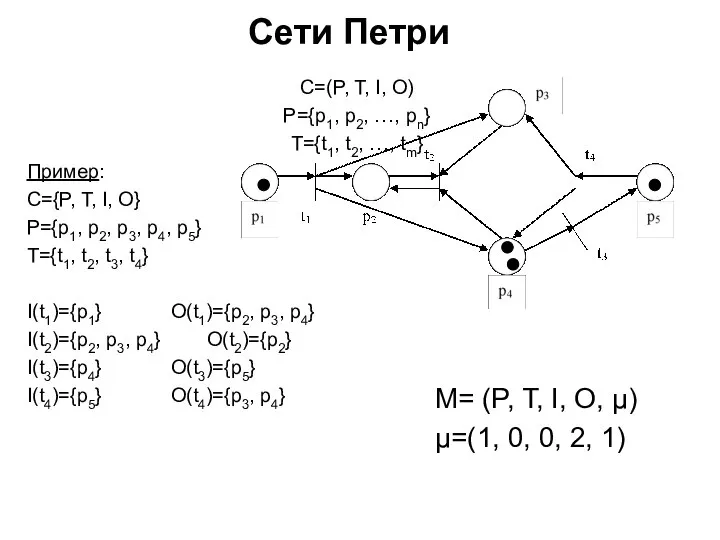 Сети Петри
Сети Петри Презентация для класса ЗАДАЧИ НА РАЗРЕЗАНИЕ
Презентация для класса ЗАДАЧИ НА РАЗРЕЗАНИЕ  Признаки равенства треугольников
Признаки равенства треугольников Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной «Распределительный закон умножения». 5 класс.
«Распределительный закон умножения». 5 класс.  Графический диктант. Математика
Графический диктант. Математика Презентация по математике "Уменьшаемое. Вычитаемое. Разность" - скачать
Презентация по математике "Уменьшаемое. Вычитаемое. Разность" - скачать  Шкалы и координаты
Шкалы и координаты Свойство биссектрисы угла
Свойство биссектрисы угла Десятичная запись дробных чисел
Десятичная запись дробных чисел Виды углов. Измерение углов
Виды углов. Измерение углов Функции многих переменных
Функции многих переменных Способы решений систем линейных уравнений
Способы решений систем линейных уравнений Теорема Фейербаха
Теорема Фейербаха ТЕОРИЯ КОНЕЧНЫХ МНОЖЕСТВ (КОМБИНАТОРИКА) §1. Принципы сложения и умножения Комбинаторика занимается подсчетом количеств разных комбинаций, которые можно получить различными способами из тех или иных конечных множеств.
ТЕОРИЯ КОНЕЧНЫХ МНОЖЕСТВ (КОМБИНАТОРИКА) §1. Принципы сложения и умножения Комбинаторика занимается подсчетом количеств разных комбинаций, которые можно получить различными способами из тех или иных конечных множеств.  Модели нелинейной регрессии
Модели нелинейной регрессии График линейной функции
График линейной функции Интеграл и его практическое применение
Интеграл и его практическое применение Отношения и пропорции
Отношения и пропорции Сложение и вычитание десятичных дробей. (Урок 111)
Сложение и вычитание десятичных дробей. (Урок 111) Правильные многогранники
Правильные многогранники Неопределённый интеграл
Неопределённый интеграл Логарифм. Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов
Логарифм. Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов Предмет, метод, задачи статистики, ее организация
Предмет, метод, задачи статистики, ее организация Построение сечений тетраэдра. (10 класс)
Построение сечений тетраэдра. (10 класс)