Теория статистических решений. Статистические игры. Игры с природой

Содержание

Слайд 2

Казанская О.В. Содержание раздела Основные понятия Игры без эксперимента Игры с

Казанская О.В.

Содержание раздела

Основные понятия
Игры без эксперимента
Игры с единичным

экспериментом
Игры с многократным экспериментом
Дерево решений при принятии решений в условиях неопределенности
Слайд 3

Казанская О.В. Список использованных источников Коршунов Ю.М. Математические основы кибернетики. М.:

Казанская О.В.

Список использованных источников

Коршунов Ю.М. Математические основы кибернетики. М.: Энергия,1980

– 424 с.
Зайченко Ю.П. Исследование операций, Киев: Высшая школа, 1975, 1988, 1993, 2001 гг.,
Таха Х. Исследование операций. 1985, 2002.
Исследование операций. Под ред. Моудера Дж., Эльмаграби С. М.: Мир, 1981г. (В 2-х томах)
Общая методика конструирования критериев оптимальности решений в условиях риска и неопределенности / Финансовый менеджмент №5 / 2002 http://www.dis.ru/fm/arhiv/2002/5/10.html
Слайд 4

Казанская О.В. Тема 1. Статистические игры. Основные понятия

Казанская О.В.

Тема 1. Статистические игры. Основные понятия

Слайд 5

Казанская О.В. 1. Основные понятия теории статистических решений В основе теории

Казанская О.В.

1. Основные понятия теории статистических решений

В основе теории антагонистических

игр – предположение о том, что интересы двух игроков противоположны, что имеет место конфликтная ситуация. В таких играх игрок действует активно в противовес интересам других игроков (если игры не кооперативные)
Слайд 6

1.1. Основные понятия теории статистических решений Во многих практических ситуациях -

1.1. Основные понятия теории статистических решений

Во многих практических ситуациях -

один из игроков нейтрален, т.е. не стремится обратить в свою пользу ошибки, совершаемые противником
В таких ситуациях сторону, выступающую в качестве объективной реальности, т.е. совокупность внешних обстоятельств (имеющих случайный неопределенный характер), в которых приходится принимать решения, принято называть «природой»
Слайд 7

1.1. Основные понятия теории статистических решений # Df 1. Модели ситуаций,

1.1. Основные понятия теории статистических решений

# Df 1. Модели ситуаций,

в которых в качестве одного из противников выступает «природа» - называют играми с «природой» или статистическими играми
Слайд 8

Казанская О.В. 1.1. Основные понятия теории статистических решений # Df 2.

Казанская О.В.

1.1. Основные понятия теории статистических решений

# Df

2. Второй участник игры с «природой» - «статистик» или ЛПР
«Природа» не совершает злого умысла по отношению к человеку («статистику»)
→ «природу» нельзя рассматривать как разумного противника, который мог бы использовать ошибки, совершаемые «статистиком»
→ в игре с «природой» есть только задача «статистика», но нет задачи «природы»
Слайд 9

Казанская О.В. 1.1. Основные понятия теории статистических решений # Df 3.

Казанская О.В.

1.1. Основные понятия теории статистических решений

# Df 3.

Задача «статистика»
Необходимо:
выработать (принять решение) с наибольшей для себя выгодой в условиях неопределенности (неполной информации) о поведении «природы»
т.к. информация неполна, т.е. есть возможность принятия ошибочного решения, нужно выработать такое решение (стратегию), которое сводит к минимуму нежелательные последствия ошибочного решения
Слайд 10

Казанская О.В. 1.1. Основные понятия теории статистических решений # Df 3.

Казанская О.В.

1.1. Основные понятия теории статистических решений

# Df 3.

Задача «статистика» Необходимо:
учитывать то, что в некоторых ситуациях можно провести эксперимент (со стоимостными и временными затратами), поэтому нужен анализ: имеет ли смысл проводить эксперимент и каковы его характеристики
Слайд 11

Казанская О.В. 1.1. Основные понятия теории статистических решений # Df 4.

Казанская О.В.

1.1. Основные понятия теории статистических решений

# Df 4.
Теория статистических

решений (ТСтР) – это теория статистических игр (игр с «природой»
ТСтР – это теория оптимального недетерминированного поведения в условиях неопределенности /МЭ, т.5, стр. 183/
ТСтР (более узко, с точки зрения математической статистики) - это теория проведения статистических наблюдений, их обработки и использования /Там же/
Слайд 12

Теория статистических решений Современная общая концепция статистического решения принадлежит А.Вальду /Вальд

Теория статистических решений

Современная общая концепция статистического решения принадлежит А.Вальду /Вальд А.

Последовательный анализ. М. 1960/
Классическая задача математической статистики – на основе качественного описания распределения вероятностей некоторой случайной величины и результатов фиксированного числа наблюдений (измерений) случайной величины необходимо сделать вывод об оценке закона распределения (и выбрать оптимальное поведение)
Слайд 13

Теория статистических решений Последовательный анализ Вальда - каждый дополнительный эксперимент имеет

Теория статистических решений

Последовательный анализ Вальда - каждый дополнительный эксперимент имеет стоимость,

ошибочное решение штрафуется.
Необходимо построить решающее правило, оптимальное в том смысле, что минимизируется математическое ожидание всех убытков
Применение последовательного анализа ведет к снижению необходимого числа наблюдений (экспериментов)
В 1820 г. Лаплас уподобил получение статистической оценки азартной игре, в которой статистик терпит поражение, если его оценки плохи
Слайд 14

Казанская О.В. Тема 2. Статистические игры без эксперимента Постановка задачи Подходы к решению

Казанская О.В.

Тема 2. Статистические игры без эксперимента Постановка задачи Подходы к решению

Слайд 15

2. Игра без эксперимента. 2.1. Постановка задачи ДАНО (блок данных B):

2. Игра без эксперимента. 2.1. Постановка задачи

ДАНО (блок данных B):
D

= {d1,d2,…,dm} – множество стратегий «статистика» (ЛПР)
S = {s1,s2,…sn} – множество состояний «природы»
L(d,s) : {ai,j} – функция потерь (выигрышей)
_______________________
Возможно ! ДАНО (блок B’):
P(S) = (p1,p2,…,pn) – вероят-ности состояний «природы»
_________________________
НАЙТИ: («чистую») стратегию поведения «статистика» (ЛПР)

ПРИМЕР:
d1 – не брать зонтик,
d2 – взять зонтик
s1 – будет дождь
s2 – будет ясно
{ai,j}=
(p1,p2) = (0,3; 0,7)

Слайд 16

Казанская О.В. Вопросы для обсуждения Какую исходную информацию в теории статистических

Казанская О.В.

Вопросы для обсуждения

Какую исходную информацию в теории статистических игр

можно считать объективной (экспертной), а какую субъективной?
Понятие чистых и смешанных стратегий в антагонистических и статистических играх, что общего? В чем различие?
Слайд 17

2. Игра без эксперимента. 2.2. Подходы к решению задачи Принцип Сэвиджа

2. Игра без эксперимента. 2.2. Подходы к решению задачи

Принцип Сэвиджа …
Принцип

Гурвица …
Принцип Лапласа …
Какие еще принципы (критерии) оптимальности используются в играх без эксперимента? Смысл их введения?
Принцип максимального правдоподобия …
Критерий «ожидаемое значение – дисперсия» …
Критерий предельного уровня …
…
Таха Х. Исследование операций
Лабскер Л.Г., Яновская Е.В. Общая методика конструирования критериев оптимальности решений в условиях риска и неопределенности // Финансовый менеджмент №5, 2002 [http://www.dis.ru/fm/arhiv/2002/5/10.html
Слайд 18

Казанская О.В. 2. Игра без эксперимента. 2.2. Подходы к решению задачи

Казанская О.В.

2. Игра без эксперимента. 2.2. Подходы к решению задачи


Принцип минимакса (критерий Вальда)
d* : L (d*) = min max L(d,s)
d s
Принцип минимальных ожидаемых потерь (критерий Байеса)
d* : ML (d*) = min ML (d),
d
где ML(d) = ∑ L(d,s)*P(s) =∑ai,j*pj
s j
- математическое ожидание потерь при выборе «статистиком» стратегии d

ПРИМЕР:
…
d* = d2 L(d*) = 50
ML(d1) =
= 100*0,3 +
+ 0*0,7 = 30
ML(d2) =
- 50*0,3 +
+ 50*0,7 = 20
d* = d2 L(d*) = 20

Слайд 19

2. Игра без эксперимента 2.2. Подходы к решению задачи Комментарии к

2. Игра без эксперимента 2.2. Подходы к решению задачи Комментарии к

принципу Байеса /Таха Х./

Нецелесообразно использовать ожидаемое значение стоимостного выражения (выигрыша или потерь) [принцип Байеса] как единственный критерий для получения решения
Этот критерий служит только ориентиром, а окончательное решение может быть принято лишь на основе всех существенных факторов
Использование данного принципа предполагает многократное решение одной и той же задачи

Слайд 20

2. Игра без эксперимента 2.2. Подходы к решению задачи Комментарии к

2. Игра без эксперимента 2.2. Подходы к решению задачи Комментарии к

принципу Байеса /Таха Х./

Математически это утверждение можно доказать следующим образом:
если X – случайная величина,
а М{X} – математическое ожидание X, то при
достаточно большом объеме выборки разница между
выборочным средним и математическим ожиданием
стремится к нулю.
Следовательно, использование данного критерия, допустимо лишь в случае, когда одно и тоже решение приходится принимать достаточно большое число раз
► Вывод !!: ориентация на ожидания будет приводить к неверным результатам для решений, которые приходится принимать небольшое число раз

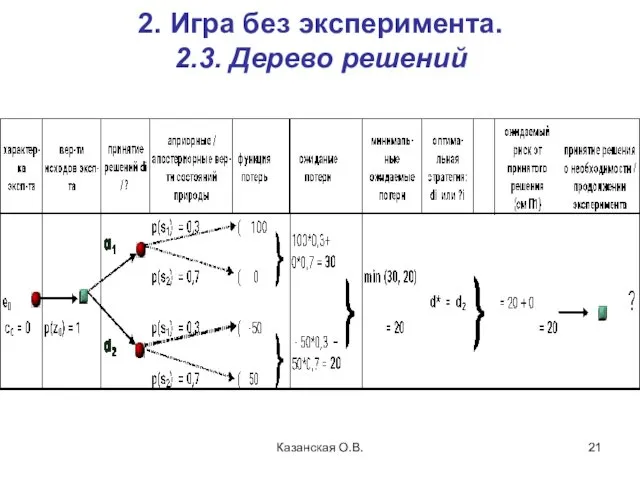
Слайд 21

Казанская О.В. 2. Игра без эксперимента. 2.3. Дерево решений

Казанская О.В.

2. Игра без эксперимента. 2.3. Дерево решений

- Предыдущая
Недвижимость у Моря! г.Сочи!
Следующая -
ОГЭ Что такое жизненные ценности

Похожие презентации

Преподаватель математики Качанова Ирина Алексеевна Степное Озеро 2013
Способы решения задачи на нахождение площади поверхности фигуры, составленной из прямоугольных параллелепипедов
Поскольку наглядно-образные компоненты мышления играют исключительно важную роль в жизни человека, то использование их в изуч
Прямая пропорциональная зависимость
Презентация по математике "Метод интервалов. Общий метод интервалов" - скачать
Взаимное расположение графиков линейной функции
Відкритий урок з математики. (4 класс)
Множества. Круги Эйлера
Одночлен и его стандартный вид
Реєстрація осіб для участі в зовнішньому незалежному оцінюванні
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Задача Коши.
Основные типы алгоритмов и формы записи
Алгоритмы на графах
Параллельные прямые
Волшебные превращения геометрических фигур (ИЗО, 1 класс)
Корень n – ой степени
Примеры решения тригонометрических уравнений
Трапеция
Решение задач 1 класс
Действия с рациональными числами. 6 класс.
Муниципальное общеобразовательное учреждение «Тарко-Салинская средняя общеобразовательная школа № 2» Обобщающий урок по теме «
Кто хочет стать миллионером. Игра для учеников 7 класса
Логарифмические неравенства. Теория и решение
Количественное описание математических объектов
Теорема Пифагора
Математический лабиринт Нить Ариадны
Сложение и вычитание дробей с разными знаменателями
Отбор корней при решении тригонометрических уравнений, используя свойство периодичности тригонометрических функций
Вы можете прислать нам Вашу презентацию и мы опубликуем ее на сайте.
Обратная связь
Для правообладателей
Email: Нажмите что бы посмотреть