Содержание
- 2. ПЛАН
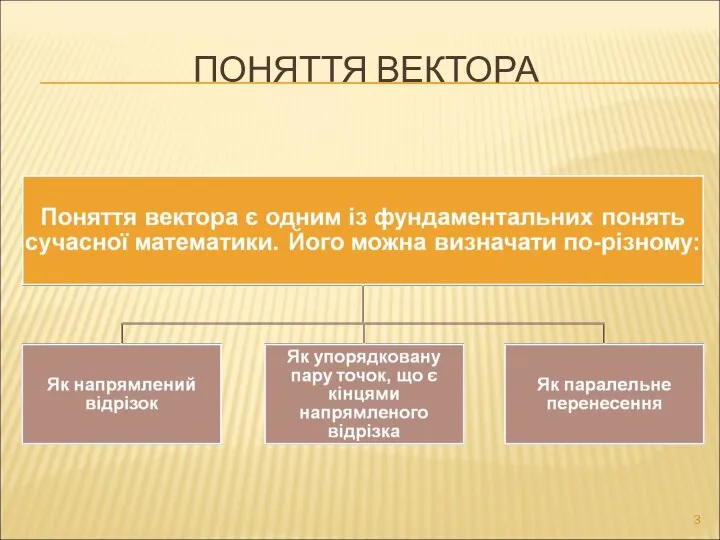
- 3. ПОНЯТТЯ ВЕКТОРА
- 4. ПОНЯТТЯ ВЕКТОРА Г. Грассман В. Гамільтон
- 5. ЗАСТОСУВАННЯ ВЕКТОРА
- 6. МАТЕМАТИЧНЕ ПОНЯТТЯ ВЕКТОРА
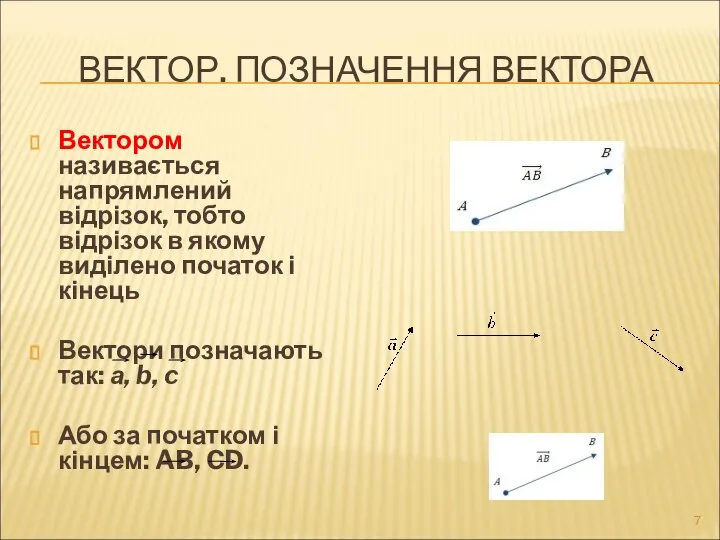
- 7. ВЕКТОР. ПОЗНАЧЕННЯ ВЕКТОРА Вектором називається напрямлений відрізок, тобто відрізок в якому виділено початок і кінець Вектори
- 8. МОДУЛЬ ВЕКТОРА Абсолютною величиною (або модулем) називається довжина відрізка, що задає вектор. Абсолютна величина нуль-вектора дорівнює
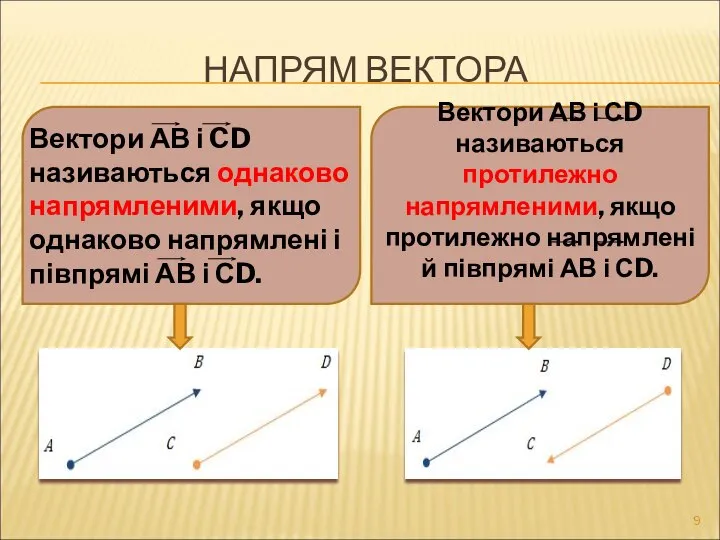
- 9. НАПРЯМ ВЕКТОРА Вектори АВ і CD називаються однаково напрямленими, якщо однаково напрямлені і півпрямі АВ і
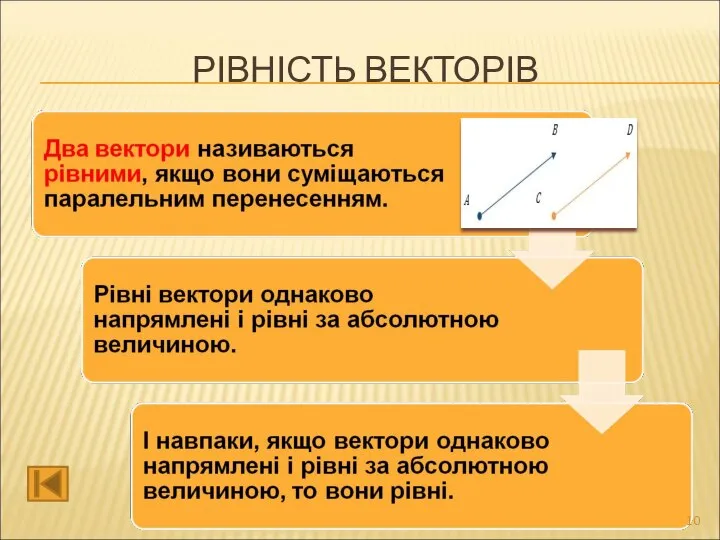
- 10. РІВНІСТЬ ВЕКТОРІВ
- 11. КООРДИНАТИ ВЕКТОРА Координатами вектора а з початком А(х1 ; у1 ) і кінцем В(х2 ; у2
- 12. ЗАДАЧА №1 Дано точки А(3;5) і В(-3;3). Знайдіть координати вектора АВ. Дано вектор а(3;4). Знайти абсолютну
- 13. РОЗВ’ЯЗАННЯ №1 АВ(-3-3;3-5) =АВ(-6;-2). Відповідь. АВ(-6;-2) ІаІ = = = Відповідь. ІаІ= 5. РОЗВ’ЯЗАННЯ №2
- 14. ДІЇ З ВЕКТОРАМИ Сумою векторів а і b з координатами а1, а2 і b1, b2 називається
- 15. ЗАДАЧА №3 Знайдіть координати вектора с, що є сумою векторів а(4;8) і b(-4;5). Нехай с(c1; с2
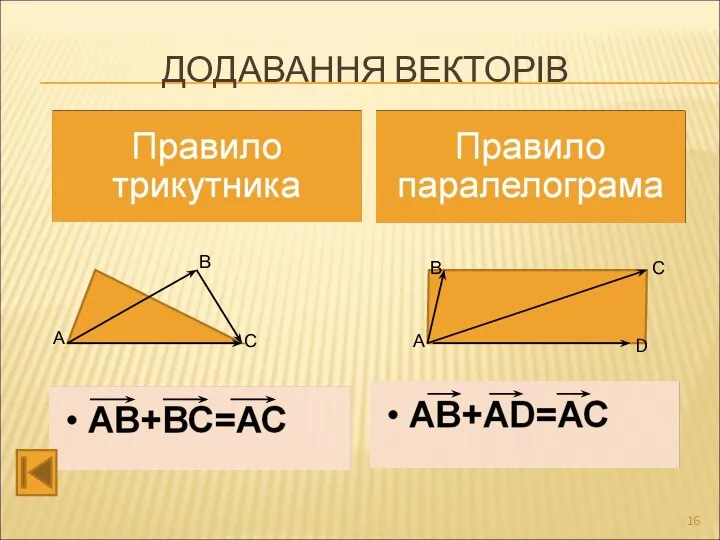
- 16. ДОДАВАННЯ ВЕКТОРІВ А В С А В С D
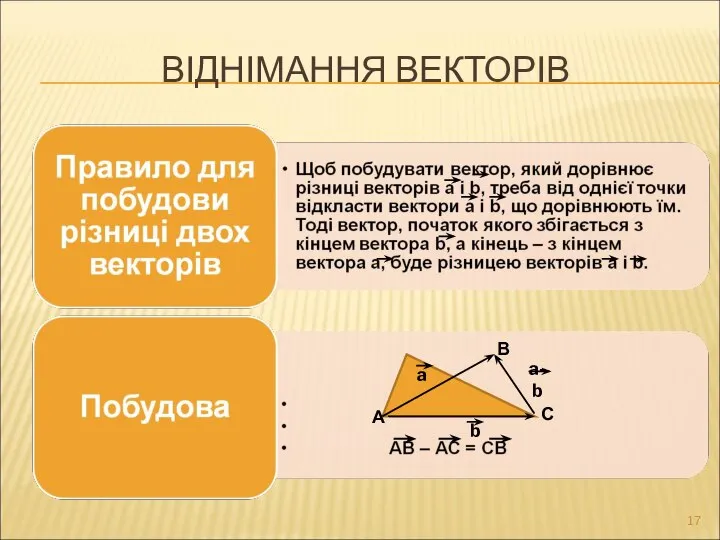
- 17. ВІДНІМАННЯ ВЕКТОРІВ А В С a a-b b
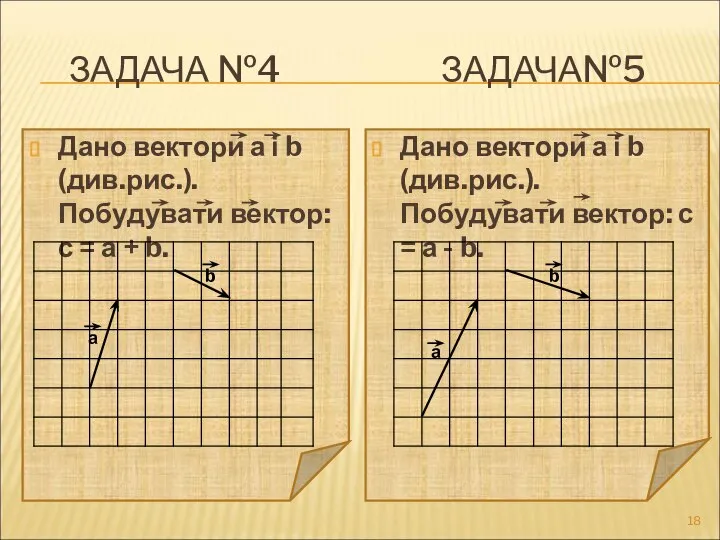
- 18. ЗАДАЧА №4 ЗАДАЧА№5 Дано вектори а і b (див.рис.). Побудувати вектор: с = а + b.
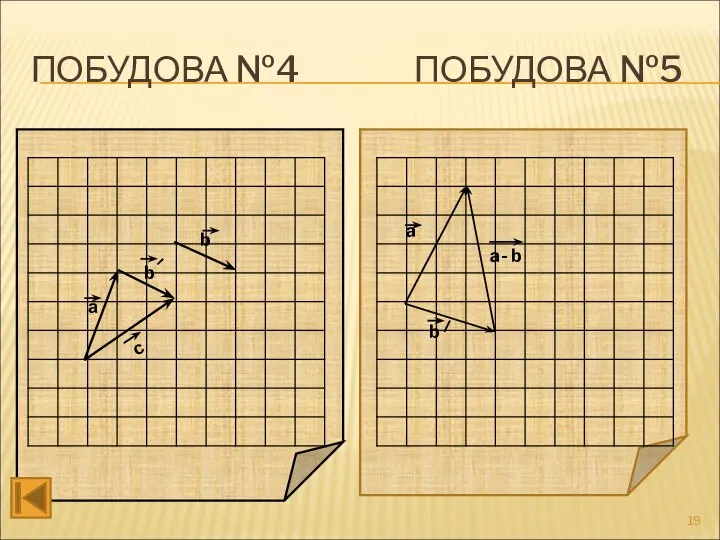
- 19. ПОБУДОВА №4 ПОБУДОВА №5 а b b c a b a- b
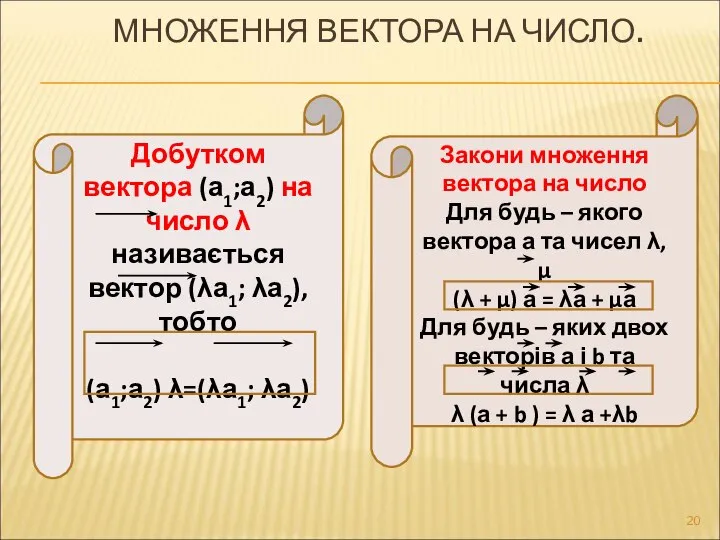
- 20. МНОЖЕННЯ ВЕКТОРА НА ЧИСЛО. Добутком вектора (а1;а2) на число λ називається вектор (λа1; λа2), тобто (а1;а2)
- 21. ЗАДАЧА №6 ЗАДАЧА №7 Дано вектори с (-3 ; 8 ) і b (4; 16). Обчислити
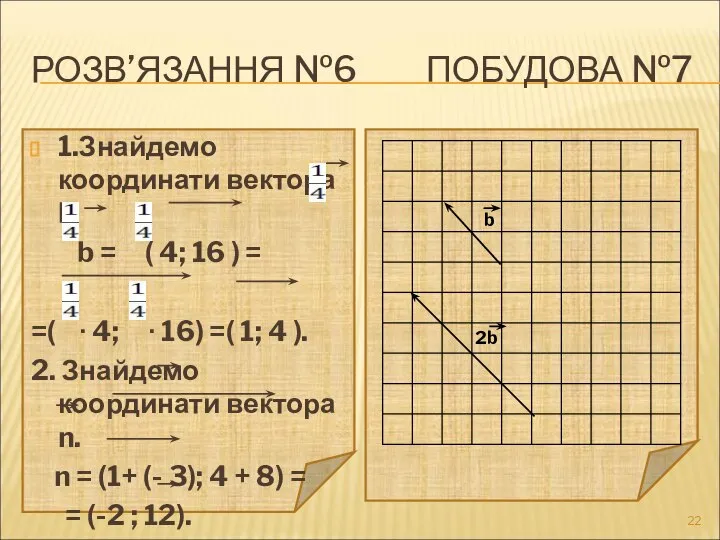
- 22. РОЗВ’ЯЗАННЯ №6 ПОБУДОВА №7 1.Знайдемо координати вектора b b = ( 4; 16 ) = =(
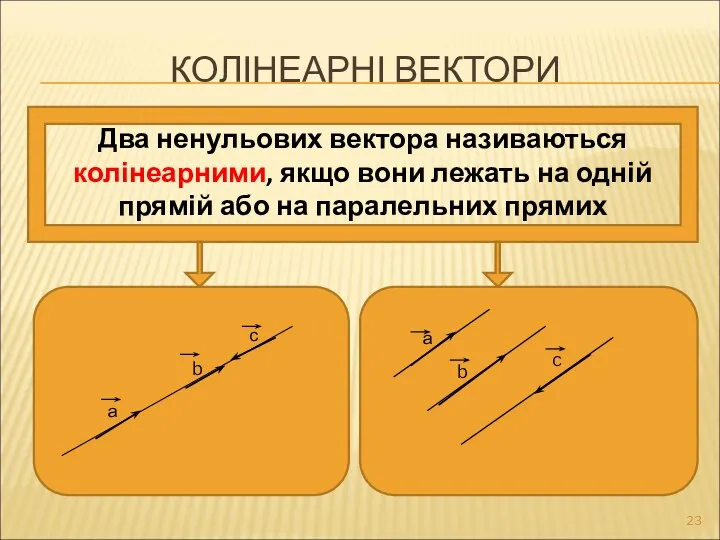
- 23. КОЛІНЕАРНІ ВЕКТОРИ Два ненульових вектора називаються колінеарними, якщо вони лежать на одній прямій або на паралельних
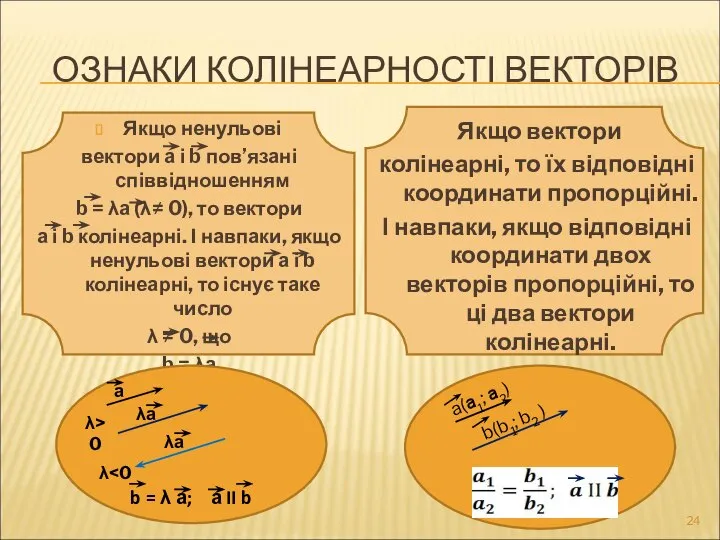
- 24. Якщо вектори колінеарні, то їх відповідні координати пропорційні. І навпаки, якщо відповідні координати двох векторів пропорційні,
- 25. ЗАДАЧА № 8 Дано чотири точки А(3;0), В(0;1), С(2;7) і D(5;6). Доведіть, що вектори АВ і
- 26. ДОВЕДЕННЯ 1.Знайдемо координати вектора АВ. АВ (0-3;1-0) =АВ(-3; 1); 2.Знайдемо координати вектора СD. СD (5 –
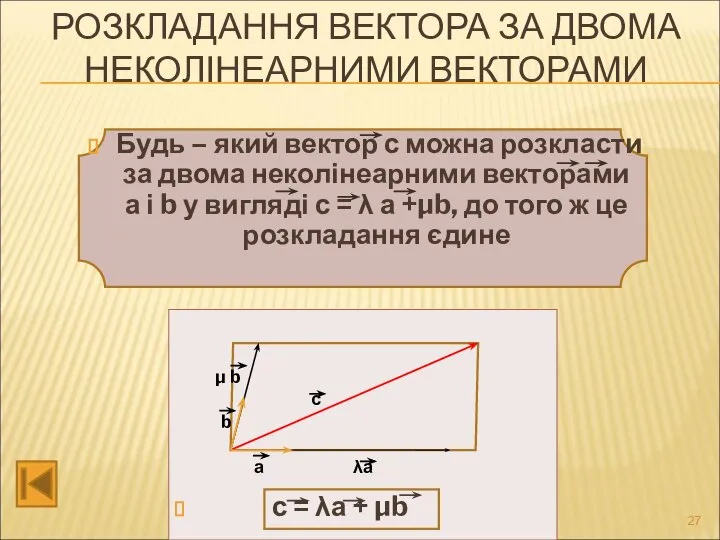
- 27. РОЗКЛАДАННЯ ВЕКТОРА ЗА ДВОМА НЕКОЛІНЕАРНИМИ ВЕКТОРАМИ с = λа + μb Будь – який вектор с
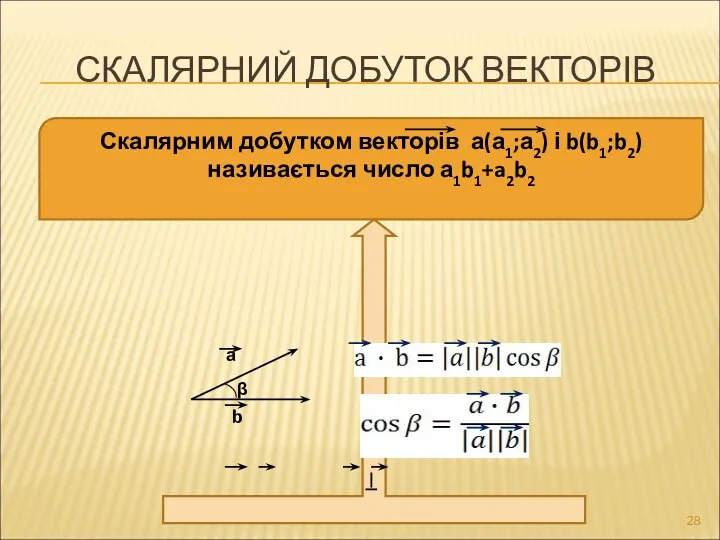
- 28. СКАЛЯРНИЙ ДОБУТОК ВЕКТОРІВ Скалярним добутком векторів а(а1;а2) і b(b1;b2) називається число а1b1+a2b2 Якщо а ∙ b
- 29. ЗАДАЧА № 9 ЗАДАЧА № 10 Знайти кут між векторами а і b, якщо І а
- 31. Скачать презентацию













 Умножаем на 2
Умножаем на 2 Сложение чисел до 15. (1 класс)
Сложение чисел до 15. (1 класс) Весь мир представлен из множества линий, которые являются для него золотым сечением.
Весь мир представлен из множества линий, которые являются для него золотым сечением. Теорема Пифагора
Теорема Пифагора Кольца. Области целостности. Поля
Кольца. Области целостности. Поля Числовые и буквенные выражения
Числовые и буквенные выражения Оптические свойства кривых второго порядка
Оптические свойства кривых второго порядка Иррациональные числа
Иррациональные числа Загадки и тайны треугольника
Загадки и тайны треугольника Параллельность прямых и плоскостей в пространстве. Лекция 2.2
Параллельность прямых и плоскостей в пространстве. Лекция 2.2 Повторение и закрепление изученного Отработать навык решения задач на нахождение части числа, числа по его части. Совершенствова
Повторение и закрепление изученного Отработать навык решения задач на нахождение части числа, числа по его части. Совершенствова Геометричні фігури
Геометричні фігури Урок -викторина «Счастливый случай». Параллельные прямые
Урок -викторина «Счастливый случай». Параллельные прямые Пирамида
Пирамида Взаимное расположение прямой и окружности. Анализ контрольной работы
Взаимное расположение прямой и окружности. Анализ контрольной работы Погрешности измерений
Погрешности измерений Деление по содержанию
Деление по содержанию Симметрия
Симметрия Объяснение выражений, записанных по условию задачи. Сравнение текстов задачи
Объяснение выражений, записанных по условию задачи. Сравнение текстов задачи Презентация на тему Рациональные числа
Презентация на тему Рациональные числа  МОЙ ЛЮБИМЫЙ УЧИТЕЛЬ
МОЙ ЛЮБИМЫЙ УЧИТЕЛЬ Решение задач В1, ОГЭ
Решение задач В1, ОГЭ Время. Единицы времени. Час. Минута. Ломаная линия. Длина ломаной
Время. Единицы времени. Час. Минута. Ломаная линия. Длина ломаной Алгебра логики. (Лекция 3)
Алгебра логики. (Лекция 3) Математическая викторина «Своя игра» для учащихся 5 классов
Математическая викторина «Своя игра» для учащихся 5 классов Понятие алгоритма. Свойства алгоритма. Способы описания алгоритмов: на естественном и алгоритмическом языках, в виде схем
Понятие алгоритма. Свойства алгоритма. Способы описания алгоритмов: на естественном и алгоритмическом языках, в виде схем Кривые второго порядка
Кривые второго порядка Формирование растра. Понятие связности пикселей. Растровое представление отрезка. Алгоритмы растризации
Формирование растра. Понятие связности пикселей. Растровое представление отрезка. Алгоритмы растризации