Содержание
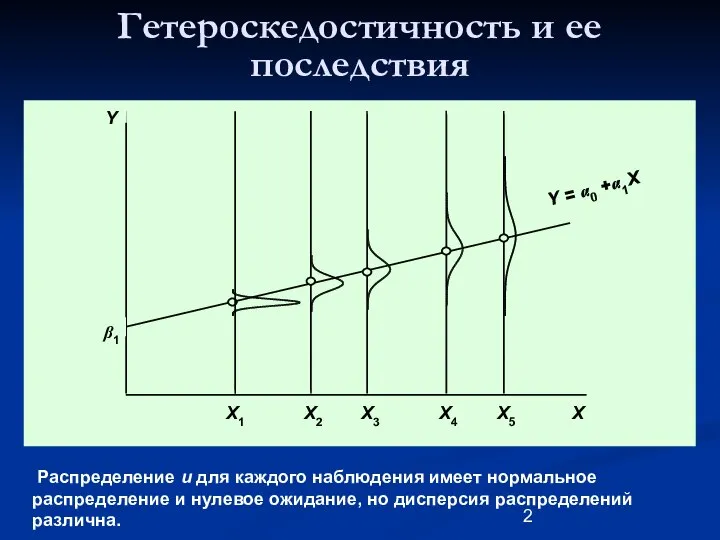
- 2. Гетероскедостичность и ее последствия β1 X Y = α0 +α1X Y Распределение u для каждого наблюдения
- 3. Гетероскедостичность и ее последствия Условия обеспечивающие гомоскедастичность (однородность) случайных возмущений: 1. Нормальное распределение случайных возмущений для
- 4. Гетероскедостичность и ее последствия В связи с тем, что оценка всех параметров модели, включая вид параметры
- 5. Методика проверки статистических гипотез Определение. Под статистической гипотезой понимается любое предположение о виде закона распределения случайной
- 6. Методика проверки статистических гипотез Алгоритм проверки статистических гипотез. Формулируется статистическая гипотеза H0. Искусственно формируется случайная величина
- 7. Методика проверки статистических гипотез Примеры. В схеме Гаусса-Маркова случайные переменные: называются дробью Стьюдента и подчиняются закону
- 8. Методика проверки статистических гипотез В схеме Гаусса-Маркова переменная: подчиняется закону распределения Фишера и критическое значение этой
- 9. Методика проверки статистических гипотез Возможные ошибки при проверке статистических гипотез. Ошибка первого рода. Когда справедливая гипотеза
- 10. Тест Готвальда-Квандта Данный тест предназначен для того, чтобы проверить гипотезу об отсутствии гетероскедастичности случайных возмущений в
- 11. Тест Готвальда-Квандта В основе теста лежат два предположения. Случайные возмущения подчиняются нормальному закону распределения. Стандартные ошибки
- 12. Алгоритм применения теста Готвальда-Квандта Шаг 1. Имеющаяся выборка из n наблюдений сортируется по возрастанию значений регрессора
- 13. Алгоритм применения теста Готвальда-Квандта Шаг 4. Для уравнений (9.1) и (9.2) вычисляются значения ESS1 и ESS3.
- 14. Алгоритм применения теста Готвальда-Квандта 5.2. Вычисленное значение GQ сравнивается с критическим значением Fкр(Pдов,n1,n3): Если GQ ≤
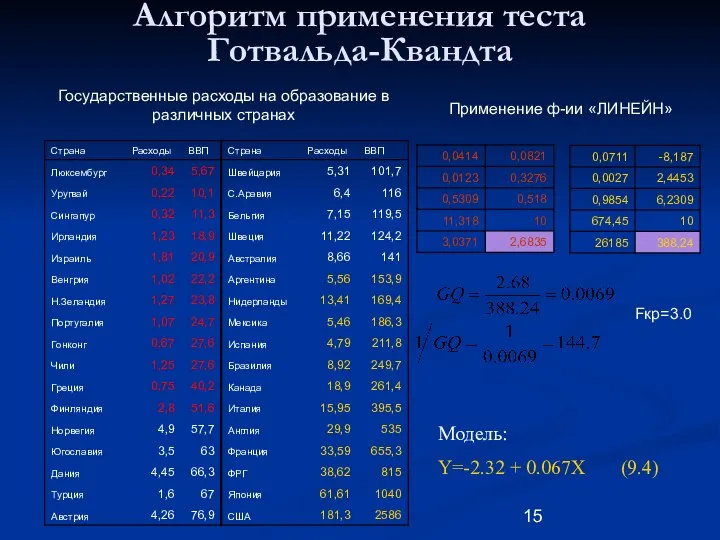
- 15. Алгоритм применения теста Готвальда-Квандта Государственные расходы на образование в различных странах Fкр=3.0 Применение ф-ии «ЛИНЕЙН» Модель:
- 16. Метод исправления гетероскедастичности Имеем: 1. Спецификацию модели: Yt=a0+a1x1t+a2x2t+a3x3t+ut (9.1) 2. Выборку наблюдений за переменными {Y,x1,x2,x3} 3.
- 17. Метод исправления гетероскедастичности Способ 1. Делится каждое уравнение наблюдений на свое σ(ut) и получается: Тогда дисперсия
- 18. Метод исправления гетероскедастичности Способ 2. Предполагаем, что σ(ut)=λxkt, где xkt регрессор «вызывающий» гетероскедастичность. Пусть для примера
- 19. Метод исправления гетероскедастичности Рассмотренные способы устранения гетероскедастичности носят название «Взвешенный метод наименьших квадратов». Теорема. Если в
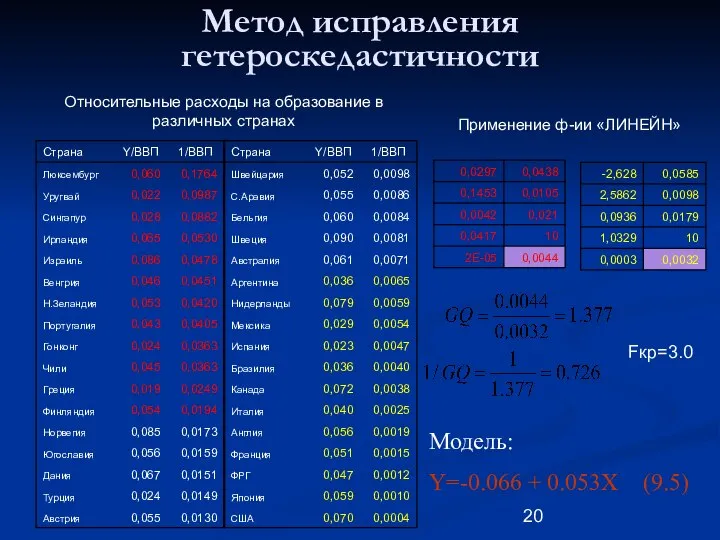
- 20. Метод исправления гетероскедастичности Применение ф-ии «ЛИНЕЙН» Относительные расходы на образование в различных странах Fкр=3.0 Модель: Y=-0.066
- 22. Скачать презентацию
















 Определители II и III порядка. Их свойства и вычисление
Определители II и III порядка. Их свойства и вычисление Метод интервалов
Метод интервалов Презентация по математике "Функция y=ax2+bx+c" - скачать
Презентация по математике "Функция y=ax2+bx+c" - скачать  Презентация Арифметические действия
Презентация Арифметические действия  Элементы алгебры логики. Математические основы информатики
Элементы алгебры логики. Математические основы информатики Линейная алгебра. Матрицы и их свойства
Линейная алгебра. Матрицы и их свойства Признаки параллельности прямых
Признаки параллельности прямых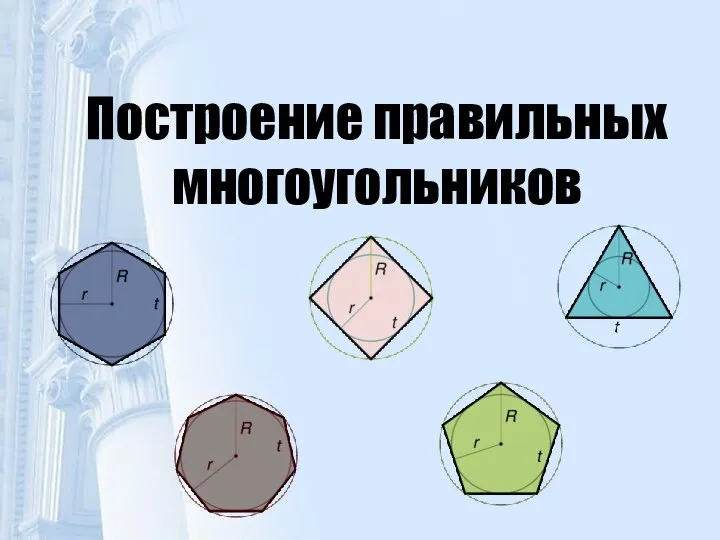 Построение правильных многоугольников
Построение правильных многоугольников Арифметическая прогрессия вокруг нас
Арифметическая прогрессия вокруг нас Варианты экзаменационных работ по математике
Варианты экзаменационных работ по математике Решение уравнений первой степени
Решение уравнений первой степени Решение примеров
Решение примеров Тема урока «Вычисление производных» Подготовил: учитель физики и математики Гребенщикова А.Г. ГОУ ТО «Тульская специальная (ко
Тема урока «Вычисление производных» Подготовил: учитель физики и математики Гребенщикова А.Г. ГОУ ТО «Тульская специальная (ко Уравнения, приводимые к квадратным
Уравнения, приводимые к квадратным Умножение натуральных чисел
Умножение натуральных чисел Презентация по математике "Угол" - скачать бесплатно
Презентация по математике "Угол" - скачать бесплатно Презентация по математике "Площадь прямоугольного треугольника" - скачать бесплатно
Презентация по математике "Площадь прямоугольного треугольника" - скачать бесплатно Углы. Математический диктант
Углы. Математический диктант Векторная алгебра. Векторы на плоскости и в пространстве
Векторная алгебра. Векторы на плоскости и в пространстве Презентация по математике "Отношения" - скачать бесплатно_
Презентация по математике "Отношения" - скачать бесплатно_ Теорема Пифагора
Теорема Пифагора Многогранники в биологии
Многогранники в биологии Математические старты
Математические старты Презентация по математике "Проценты в школьном курсе математики" - скачать
Презентация по математике "Проценты в школьном курсе математики" - скачать  Четырехугольники. Решение задач
Четырехугольники. Решение задач Наибольший общий делитель. Взаимно простые числа
Наибольший общий делитель. Взаимно простые числа Неравенства. Тест
Неравенства. Тест Уравнения. 5 класс
Уравнения. 5 класс