Содержание
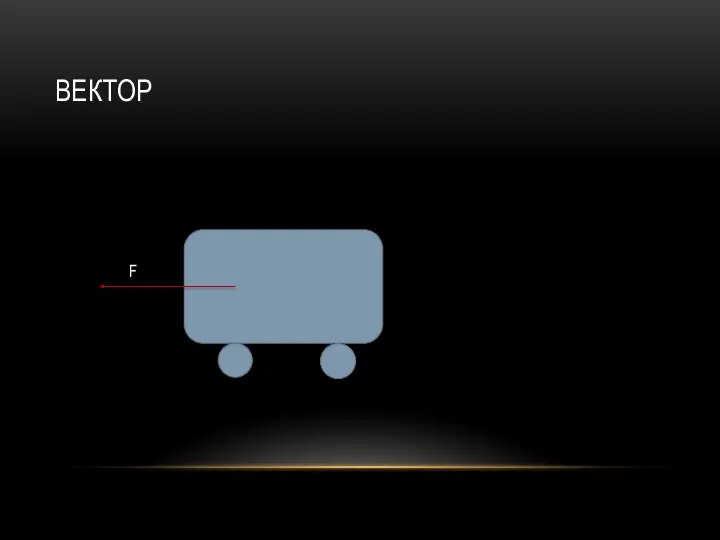
- 2. СКАЛЯРЫ. ПОНЯТИЕ ВЕКТОРА. Мы знаем, что есть 2 вида величин. Например, длина, площадь, объем, масса и
- 3. ВЕКТОР F
- 4. ВЕКТОРЫ В ГЕОМЕТРИИ Аналогично можно ввести понятие геометрического вектора. В отличие от физических векторов, векторы в
- 5. НАЧАЛО И КОНЕЦ ВЕКТОРА Любой отрезок имеет 2 конца. Назовем один из этих концов начальной точкой,
- 6. РАВЕНСТВО ВЕКТОРОВ Длину отрезка АВ называют модулем вектора AB и обозначают так: |AB|. Аналогично, модуль (длина)
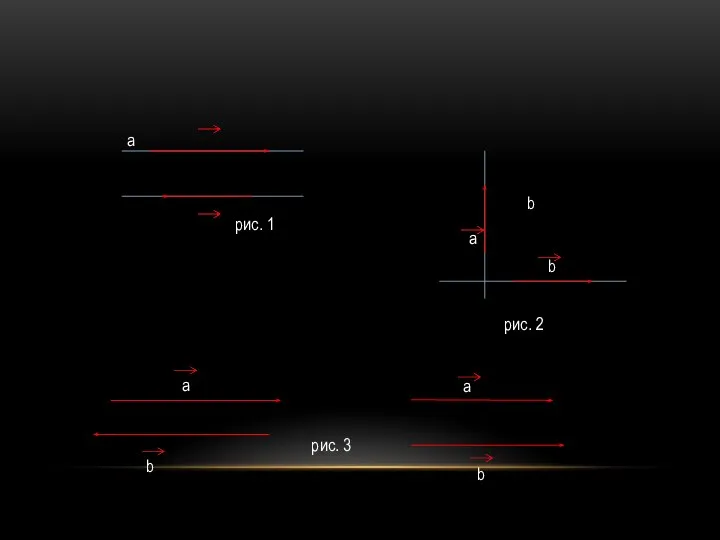
- 7. а b рис. 1 а b а b рис. 2 рис. 3 b а
- 8. Если векторы а и b лежат на перпендикулярных прямых, то их называют перпендикулярными (ортогональными) векторами и
- 9. Векторы называются равными, если они сонаправлены и их модули равны. Иными словами, если a b и
- 10. СВОЙСТВА РАВНЫХ ВЕКТОРОВ Теорема. Равные векторы можно совместить параллельным переносом, и, обратно, если векторы совмещаются парллельным
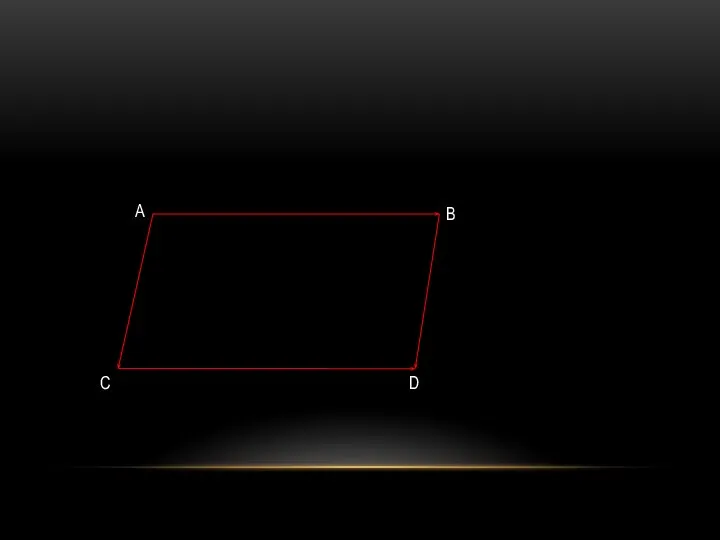
- 11. А C D B
- 12. СЛЕДСТВИЯ Следствие 1. Если АВ=СD, то АС=ВD. Если точка А является началом вектора а, то говорят,
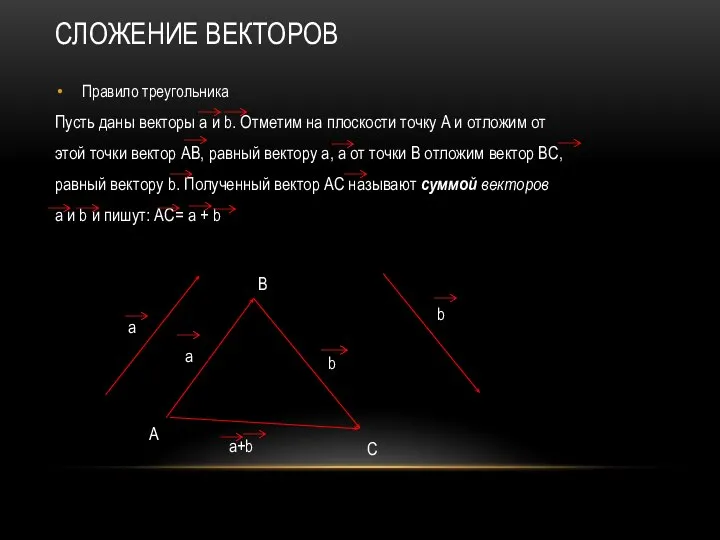
- 13. СЛОЖЕНИЕ ВЕКТОРОВ Правило треугольника Пусть даны векторы а и b. Отметим на плоскости точку А и
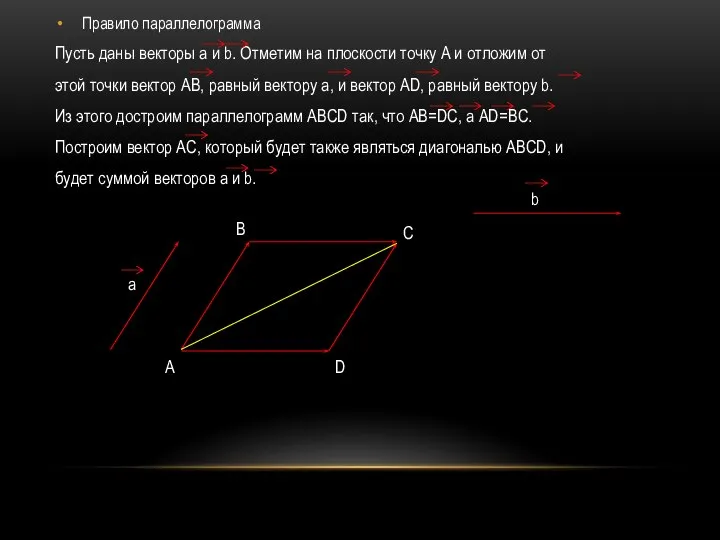
- 14. Правило параллелограмма Пусть даны векторы а и b. Отметим на плоскости точку А и отложим от
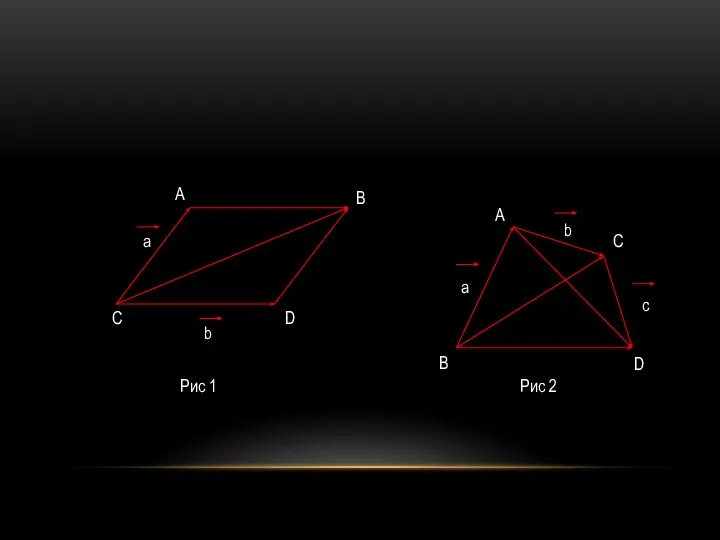
- 15. СВОЙСТВА СЛОЖЕНИЯ ВЕКТОРОВ Теорема 1. Для любых векторов a, b и c верно: 1) а+b=b+a (переместительный
- 16. Рис 1 Рис 2 C D B А a b c a D B C А
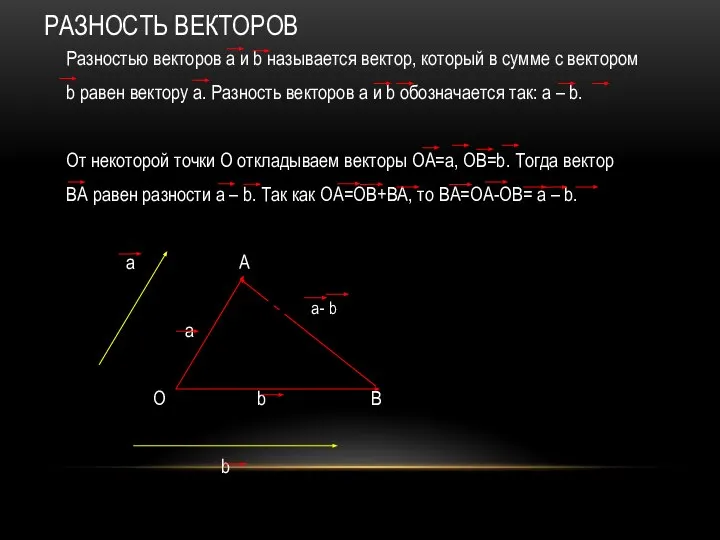
- 17. РАЗНОСТЬ ВЕКТОРОВ Разностью векторов а и b называется вектор, который в сумме с вектором b равен
- 18. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО Произведением вектора а≠0 на число k называется вектор, модуль которого равен числу
- 19. ПРИЗНАК КОЛЛИНЕАРНОСТИ ВЕКТОРОВ Теорема. Чтобы вектор b был коллинеарен ненулевому вектору а, необходимо и достаточно существование
- 20. УГОЛ МЕЖДУ ВЕКТОРАМИ Углом между векторами АВ и АС называется угол ВАС. Углом между ненулевыми векторами
- 21. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 22. ДОПОЛНОИТЕЛЬНАЯ ИНФОРМАЦИЯ. ИСТОРИЯ ВЕКТОРОВ. Раздел математики, изучающий векторы и действия над ними называется векторной алгеброй. Основные
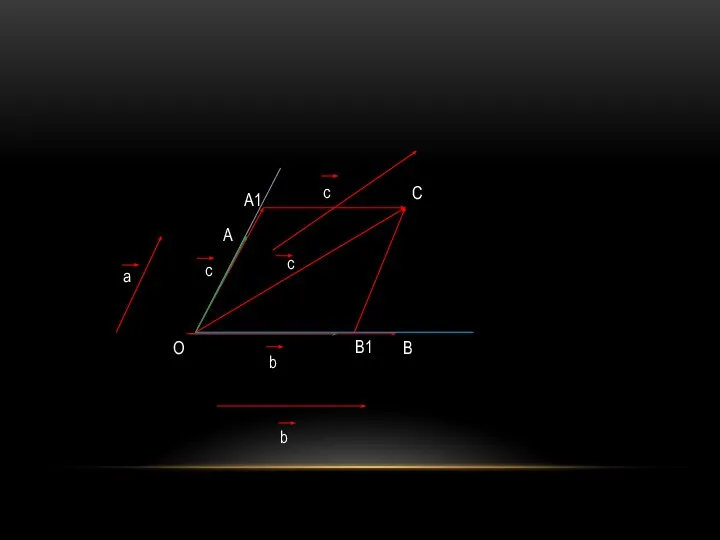
- 23. РАЗЛОЖЕНИЕ ВЕКТОРА ПО ДВУМ НЕКОЛЛИНЕАРНЫМ Теорема. Если ненулевые векторы а и b не коллинеарны, то для
- 24. B1 O C b b c a c B c A A1
- 25. КООРДИНАТЫ ВЕКТОРА В ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ Рассмотрим прямоугольную систему координат Оху. Пусть i- единичный вектор, сонаправленнный
- 26. СВОЙСТВА КООРДИНАТ ВЕКТОРА 1. У равных векторов соответствующие координаты равны: если а= (х; у), b= (u;
- 27. РАДИУС-ВЕКТОР. КООРДИНАТНЫЙ ВИД СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ. Если на плоскости Оху задана точка А (х;у), то вектор ОА
- 28. КООРДИНАТНЫЙ ВИД КОЛЛИНЕАРНОСТИ И ПЕРПЕНДИКУЛЯРНОСТИ ВЕКТОРОВ. ОПРЕДЕЛЕНИЕ УГЛА МЕЖДУ ВЕКТОРАМИ.
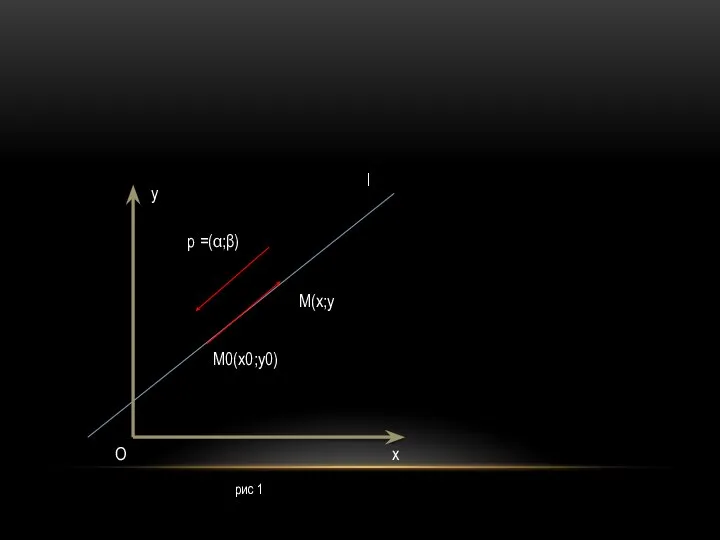
- 29. УРАВНЕНИЕ ПРЯМОЙ. НАПРАВЛЯЮЩИЙ ВЕКТОР И ВЕКТОР НОРМАЛИ ПРЯМОЙ. Уравнение прямой можно задать различными способами. Например, в
- 30. рис 1 у M(x;y M0(x0;y0) O х p =(α;β) l
- 32. Скачать презентацию




















 Решение задач на смеси и растворы с помощью уравнений
Решение задач на смеси и растворы с помощью уравнений Предикаты и кванторы. Действия над предикатами и их свойства
Предикаты и кванторы. Действия над предикатами и их свойства Угол между плоскостями. (Урок 3. Решаем С2 ЕГЭ. 11класс)
Угол между плоскостями. (Урок 3. Решаем С2 ЕГЭ. 11класс) Преобразование графиков. 8 класс
Преобразование графиков. 8 класс Планиметрия. Четырёхугольники
Планиметрия. Четырёхугольники Задачи на готовых чертежах (Теорема Пифагора)
Задачи на готовых чертежах (Теорема Пифагора) Возникновение понятия натурального числа. Освоение количественных представлений
Возникновение понятия натурального числа. Освоение количественных представлений Начертательная геометрия. Пересечение поверхности плоскостью частного положения. (Лекция 5)
Начертательная геометрия. Пересечение поверхности плоскостью частного положения. (Лекция 5) Системы счисления
Системы счисления Проверочная работа. Деление с остатком
Проверочная работа. Деление с остатком Теорема Эйлера
Теорема Эйлера Урок математики 4 класс Тема: «Площадь прямоугольного треугольника» Выполнила: учитель начальных классов МБОУ СОШ №16 г. Иши
Урок математики 4 класс Тема: «Площадь прямоугольного треугольника» Выполнила: учитель начальных классов МБОУ СОШ №16 г. Иши Математики России
Математики России Целые и дробные числа
Целые и дробные числа Статистические и аналитические методы оцеки рисков
Статистические и аналитические методы оцеки рисков Алгебра және анализ бастамалары пәні. 10 сынып
Алгебра және анализ бастамалары пәні. 10 сынып Тренажёр. Таблица умножения. «С Барби за покупками»
Тренажёр. Таблица умножения. «С Барби за покупками» Применение вероятностных методов в технике Выполнила: студентка гр.СО-11 Третьяк Юлия
Применение вероятностных методов в технике Выполнила: студентка гр.СО-11 Третьяк Юлия  Параллельные прямые в пространстве
Параллельные прямые в пространстве Применение симметрии при решении алгебраических задач Учениц 10И класса: Коротковой Анастасии Журавлёвой Дарьи Руководитель:
Применение симметрии при решении алгебраических задач Учениц 10И класса: Коротковой Анастасии Журавлёвой Дарьи Руководитель:  Перестановка слагаемых. Применение переместительного свойства
Перестановка слагаемых. Применение переместительного свойства Перемасштабирование каротажных диаграмм
Перемасштабирование каротажных диаграмм Презентация на тему Сложение двузначных чисел урок - сказка
Презентация на тему Сложение двузначных чисел урок - сказка  Нахождение конуса в природе
Нахождение конуса в природе Решение задач на нахождение площади
Решение задач на нахождение площади Геометрические тела
Геометрические тела Тела и поверхности вращения
Тела и поверхности вращения «Путешествие в страну обыкновенных дробей»
«Путешествие в страну обыкновенных дробей»