Содержание
- 2. Властивість 1. Значення визначника не змінюється при транспонуванні. Приклад 1. Наслідок. У визначнику рядки та стовпці
- 3. Властивість 3. Визначник, стовпець якого складається з нулів, дорівнює нулеві. Приклад 3 Властивість 4. Визначник, що
- 4. Властивість 5. Визначник, що має два пропорційні стовпці, дорівнює нулю. Приклад 5 Властивість 6. Визначник зросте
- 5. Властивість 7. Значення визначника не зміниться, якщо до елементів якогось стовпця додати (відняти) відповідні елементи іншого
- 6. Властивість 8. Якщо у визначнику елементи i-го рядка є сумою двох доданків, то він дорівнює сумі
- 7. Для обчислення визначників порядку використовують алгебраїчні доповнення Правило обчислення визначника n- го порядку. Мінори та алгебраїчні
- 8. Правило обчислення визначника n- го порядку. Приклад 9 Знайти алгебраїчні доповнення елементів a21 та a33 визначника
- 9. Приклад 10 Правило обчислення визначника n- го порядку. Записати алгебраічне доповненя елемента a23 визначника Розв’язок А23
- 10. Правило. Розклад визначника за елементами рядка (стовпця). (теорема Лапласа (23.03.1747-5.03.1827)). Визначник n-го порядку дорівнює сумі добутків
- 11. Обчислення визначника порядку n≥3 . Приклад 11
- 12. Обернена матриця. Матрицю А-1 називають оберненою до матриці А, якщо виконуються рівності А× А-1 = А-1×А
- 13. Обернена матриця. Знайти матрицю, обернену до матриці Приклад 12 1) Обчислюємо значення визначника матриці А Розв’язок
- 14. 3) Записуємо обернену до А матрицю Приклад 12 (продовження)
- 15. Системи лінійних рівнянь Систему алгебраїчних рівнянь називають лінійною, якщо вона може бути записана у вигляді де
- 16. Системи лінійних рівнянь Розв’язком системи називають множину дійсних чисел с1, с2, …, сn, підстановка яких у
- 17. Системи лінійних рівнянь Знаходження єдиного розв’язку Системи n лінійних рівнянь з n невідомими . С. Л.
- 18. Системи n лінійних рівнянь з n невідомими Метод Крамера. Цей визначник отримано шляхом послідовної заміни j-го
- 19. Приклад 13 Розв’язати систему лінійних рівнянь за формулами Крамера: Розв’язок ∆ ≠ 0, можемо застосувати правило
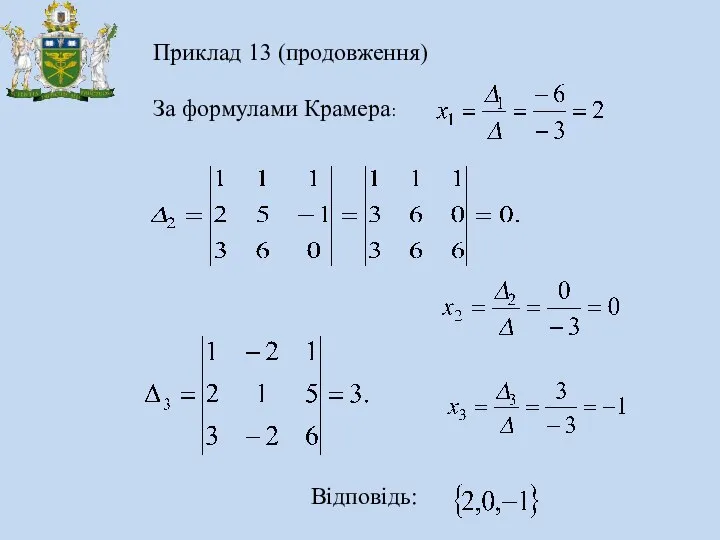
- 20. Приклад 13 (продовження) За формулами Крамера: Відповідь:
- 21. Системи n лінійних рівнянь з n невідомими Метод оберненої матриці. то С.Л. Р. , згідно з
- 22. Приклад 14 Розв’язати C.Л.Р. методом оберненої матриці Запишемо систему рівнянь у вигляді матричного рівняння Розв’язок де
- 23. Приклад 14 (продовження) Знаходимо алгебраїчні доповнення:
- 24. Приклад 14 (продовження) Запишемо обернену матрицю до матриці А
- 26. Скачать презентацию






















 Эластичности и логарифмические модели
Эластичности и логарифмические модели Взаимно обратные числа. 6 класс
Взаимно обратные числа. 6 класс Модуль «АЛГЕБРА» №7 Автор презентации: Гладунец Ирина Владимировна учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой об
Модуль «АЛГЕБРА» №7 Автор презентации: Гладунец Ирина Владимировна учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой об Матрицы. Виды и действия над матрицами
Матрицы. Виды и действия над матрицами Итоговое повторение. 9 класс (2)
Итоговое повторение. 9 класс (2) Применение интеграла для нахождения площадей объектов ландшафтного дизайна
Применение интеграла для нахождения площадей объектов ландшафтного дизайна Числа. Количественные числительные от 6 до 10
Числа. Количественные числительные от 6 до 10 Аттестационная работа. Решение логарифмических неравенств
Аттестационная работа. Решение логарифмических неравенств Среднее арифметическое
Среднее арифметическое Кольорові числа Х. Кюізенера
Кольорові числа Х. Кюізенера МАТЕМАТИКА 1 КЛАСС УЧИТЕЛЬ: Федчишина Милана Вадимовна МОУ СОШ № 31
МАТЕМАТИКА 1 КЛАСС УЧИТЕЛЬ: Федчишина Милана Вадимовна МОУ СОШ № 31 Презентация по математике "Умножение положительных и отрицательных чисел" - скачать
Презентация по математике "Умножение положительных и отрицательных чисел" - скачать  Можно ли измерить длину окружности?
Можно ли измерить длину окружности? Классическая теория вероятности. 6 и 11 класс
Классическая теория вероятности. 6 и 11 класс Презентация по математике "Задачи по математике для 4 класса" - скачать бесплатно
Презентация по математике "Задачи по математике для 4 класса" - скачать бесплатно Десятичнвя дробь в виде смешанного числа
Десятичнвя дробь в виде смешанного числа Уроки математики с любимыми героями. Простые множители
Уроки математики с любимыми героями. Простые множители Скрещивающиеся прямые
Скрещивающиеся прямые Прямая и окружность
Прямая и окружность Линия тождественных преобразований в курсе алгебры
Линия тождественных преобразований в курсе алгебры Квадратный корень из дроби
Квадратный корень из дроби Искусственные и нечеткие нейронные сети
Искусственные и нечеткие нейронные сети Числовые выражения, содержащие знаки + и -
Числовые выражения, содержащие знаки + и - Решение иррациональных уравнений обобщающее повторение
Решение иррациональных уравнений обобщающее повторение Примеры задач линейного программирования
Примеры задач линейного программирования Развитие познавательного интереса при обучении математике
Развитие познавательного интереса при обучении математике Координатная плоскость (часть 3)
Координатная плоскость (часть 3) Объемы прямой призмы и цилиндра. (ЕГЭ. Задачи В10, В1)
Объемы прямой призмы и цилиндра. (ЕГЭ. Задачи В10, В1)