Содержание
- 2. Цель Научиться решать геометрические задачи, которые приводят к появлению вневписанной окружности, и составить алгоритм их решения.
- 3. Задачи 1. Ввести определение вневписанной окружности треугольника и рассмотреть ее свойство. 2.Проанализировать какие задачи в ОГЭ
- 4. Понятие вневписанной окружности Определение: Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений
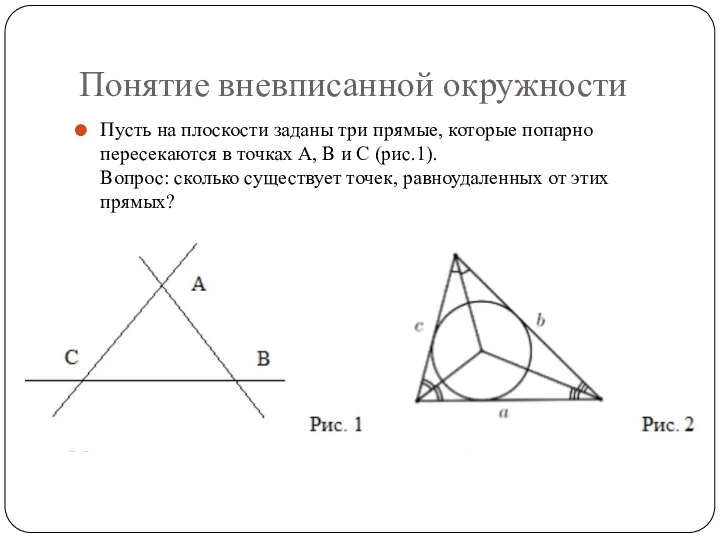
- 5. Понятие вневписанной окружности Пусть на плоскости заданы три прямые, которые попарно пересекаются в точках A, B
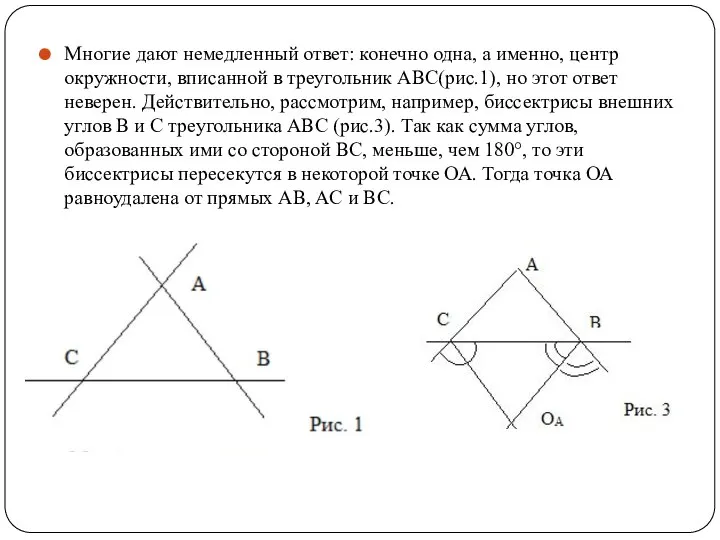
- 6. Многие дают немедленный ответ: конечно одна, а именно, центр окружности, вписанной в треугольник ABC(рис.1), но этот
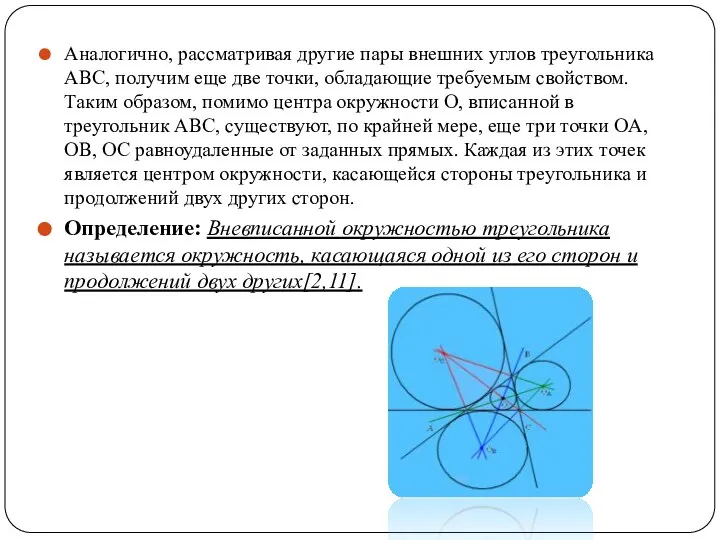
- 7. Аналогично, рассматривая другие пары внешних углов треугольника ABC, получим еще две точки, обладающие требуемым свойством. Таким
- 8. Свойство вневписанной окружности Свойство: Центр вневписанной окружности в треугольник есть точка пересечения биссектрисы внутреннего угла треугольника,
- 9. Свойство вневписанной окружности Доказательство: Т. к. окружность касается сторон угла САК, то центр окружности О равноудален
- 10. Вневписанная окружность в задачах По итогам ОГЭ прошлого года многие девятиклассники даже не приступали к решению
- 11. Задача 1. Алгоритм решения 1. Обозначить О – центр вневписанной окружности, Q – центр окружности, вписанной
- 12. Задача 2. Алгоритм решения 1. Обозначить Q – центр вневписанной окружности, О – центр окружности, вписанной
- 13. Задача 2. Алгоритм решения 5. Рассмотреть подобные прямоугольные треугольники ANO и АМQ и найти коэффициент подобия
- 14. Задача 2. Алгоритм решения 8. Рассмотреть прямоугольный треугольник SВК, в котором по теореме Пифагора r2 =
- 15. Задача 3. Алгоритм решения 1. Обозначить М – центр вневписанной окружности, О – центр вписанной окружности
- 16. ЗАДАЧА 1. Нахождение радиуса окружности вписанного в треугольник. (Демонстрационный вариант 2018г., КИМ[7]) «Основание АС равнобедренного треугольника
- 17. ЗАДАЧА 1. Нахождение радиуса окружности вписанного в треугольник. (Демонстрационный вариант 2018г., КИМ[7]) ∆AQO – прямоугольный треугольник,
- 18. ЗАДАЧА 2. Нахождение радиуса окруж - ности описанной около треугольника. (Решу ОГЭ[9]) «Две касающиеся внешним образом
- 19. ЗАДАЧА 2. Нахождение радиуса окруж - ности описанной около треугольника. (Решу ОГЭ[9]) Решение: Пусть Q –
- 20. ЗАДАЧА 2. Нахождение радиуса окруж - ности описанной около треугольника. (Решу ОГЭ[9]) Отрезки МС, СК и
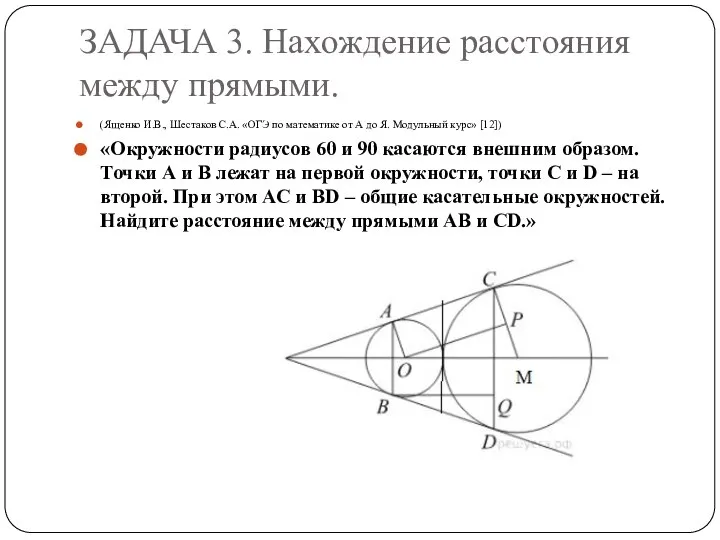
- 21. ЗАДАЧА 3. Нахождение расстояния между прямыми. (Ященко И.В., Шестаков С.А. «ОГЭ по математике от А до
- 22. ЗАДАЧА 3. Нахождение расстояния между прямыми. (Ященко И.В., Шестаков С.А. «ОГЭ по математике от А до
- 23. ЗАКЛЮЧЕНИЕ В результате проделанной работы я выяснила, что собой представляют вневписанные окружности треугольника, каким свойством они
- 25. Скачать презентацию

















 Решение квадратных уравнений различного вида разными способами
Решение квадратных уравнений различного вида разными способами Подобные треугольники
Подобные треугольники Статистика в медико-биологических исследованиях
Статистика в медико-биологических исследованиях Нумерация многозначных чисел. Сложение и вычитание многозначных чисел. Решение уравнений и задач
Нумерация многозначных чисел. Сложение и вычитание многозначных чисел. Решение уравнений и задач Час веселой математики. Внеклассное мероприятие для 5-6 классов
Час веселой математики. Внеклассное мероприятие для 5-6 классов Метод координат
Метод координат Функция её свойства и график. Урок 2
Функция её свойства и график. Урок 2 Статистические характеристики
Статистические характеристики 2.1. Матрицы
2.1. Матрицы Внеклассное занятие. Математический брейн-ринг
Внеклассное занятие. Математический брейн-ринг В этом проекте мы предложим вам на чуть – чуть побыть настоящим рыцарем и победить своего соперника. Для этого давайте поиграем в к
В этом проекте мы предложим вам на чуть – чуть побыть настоящим рыцарем и победить своего соперника. Для этого давайте поиграем в к Презентация по математике "Математика 4 класс «Деление»" - скачать бесплатно
Презентация по математике "Математика 4 класс «Деление»" - скачать бесплатно Частини величини. Дроби з чисельником 1 як частина цілого. Утворення і запис
Частини величини. Дроби з чисельником 1 як частина цілого. Утворення і запис Основы теории вероятностей или случайные события ( лекция 2)
Основы теории вероятностей или случайные события ( лекция 2) Изображение точек на координатной плоскости
Изображение точек на координатной плоскости Определение производной. Её геометрический и физический смысл
Определение производной. Её геометрический и физический смысл Презентация по математике "Основные элементы в структуре повседневного урока математики" - скачать
Презентация по математике "Основные элементы в структуре повседневного урока математики" - скачать  Примеры задач линейного программирования
Примеры задач линейного программирования Алгебра логики и таблицы истинности. (лекция 4)
Алгебра логики и таблицы истинности. (лекция 4) Понятие логарифма
Понятие логарифма Самый умный
Самый умный Моделирование систем и процессов. Свойства, классификация математических моделей. Марковские случайные процессы. (Лекция 1)
Моделирование систем и процессов. Свойства, классификация математических моделей. Марковские случайные процессы. (Лекция 1) Вертикальные углы
Вертикальные углы Правила суммы и произведения. Перестановки и подстановки
Правила суммы и произведения. Перестановки и подстановки Презентация по математике "МАТЛОГИКА" - скачать
Презентация по математике "МАТЛОГИКА" - скачать  Лист посвящен квадратам
Лист посвящен квадратам Решение задач на проценты
Решение задач на проценты Математика XIX ст. Жан Батист Жозеф Фур'є
Математика XIX ст. Жан Батист Жозеф Фур'є