Содержание
- 2. Понятие функции. Способы задания функций Пусть X – некоторое множество действительных чисел.
- 3. Определение. Если каждому элементу x из множества X по некоторому закону f ставится в соответствие вполне
- 4. Множество X называется областью определения функции f(x) и обозначается D(f ). Множество всех значений y функции
- 5. Например, для функции y = sin x область определения D(f ) = R, область значений E(f
- 6. Различают следующие способы задания функции: табличный, графический, аналитический (с помощью формул).
- 7. Под графиком функции понимают множество точек плоскости, абсциссы которых есть значения независимой переменной, а ординаты равны
- 8. К основным элементарным функциям относятся: y = xa (при постоянном a ∊ R) – степенная функция;
- 9. y = sin x, y = cos x, y = tg x, y = ctg x
- 10. Функция, заданная последовательной цепью нескольких функций (y = f(u), где u = φ(x)), называется сложной функцией.
- 11. Функции, образованные из основных элементарных функций посредством конечного числа алгебраических операций и взятия функции от функции,
- 12. Все остальные функции называются неэлементарными. Примером неэлементарной функции может служить функция вида
- 13. Функция, определяемая уравнениями в которых зависимость между y и x устанавливается посредством третьей переменной t, называется
- 14. Например, уравнения определяют линейную функцию
- 15. Предел числовой последовательности. Предел функции
- 16. Определение. Число A называется пределом последовательности a1, a2, …,an,…, если для любого положительного числа ε существует
- 17. Если последовательность a1, a2, …an,… имеет своим пределом число A, то это записывается следующим образом: или
- 18. Определение. Число А называется пределом функции y = f(x) при x → a (в точке x
- 19. Обозначают этот факт так:
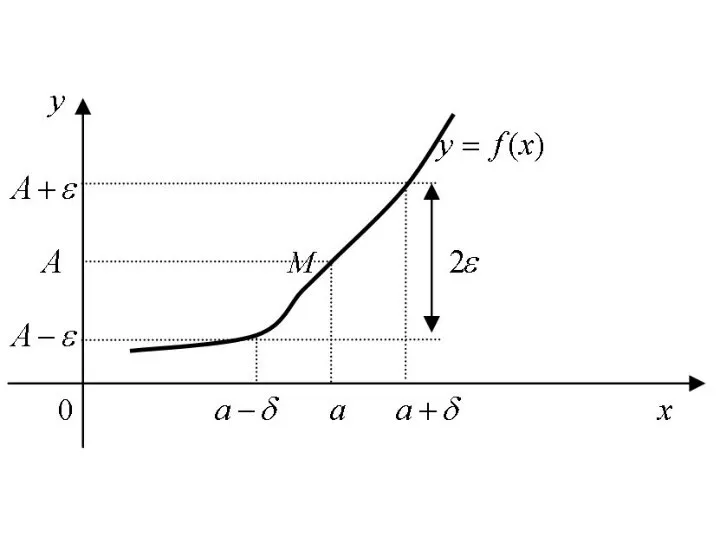
- 20. Если число A является пределом функции y = f(x) при x → a, то на графике
- 21. Так как из неравенства 0
- 23. Число A называется пределом функции y = f(x) при x → ±∞, если для любого ε
- 24. Функция y = f(x) называется ограниченной в области D, если существует постоянное число M > 0,
- 25. Например, функция ограничена для всех x ∊ R, так как в этой области |f(x)| ≤ 2.
- 26. Бесконечно малые и бесконечно большие функции
- 27. Определение. Функция α(x) называется бесконечно малой при x → a, если Функция β(x) называется бесконечно большой
- 28. Например, функция y = sin x является бесконечно малой при x → 0, а функция есть
- 29. Теорема. Если функция α(x) – бесконечно малая при x → a, то — бесконечно большая функция
- 30. Если функция β(x) – бесконечно большая при x → a, то – бесконечно малая функция при
- 31. Справедливы следующие утверждения: Сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
- 32. Произведение ограниченной функции на бесконечно малую есть бесконечно малая функция. Произведение конечного числа бесконечно малых функций
- 33. Теоремы о пределах Если пределы и существуют и конечны, то
- 34. 1) где с = const; 2)
- 35. 3) 4) где
- 36. Замечательные пределы Первый замечательный предел:
- 37. Второй замечательный предел: где e — иррациональное число, e ≈ 2,718281828 — одна из фундаментальных величин
- 38. Функция y = ex = exp(x) называется экспонентой; y = loge x = ln x называется
- 39. Пример. Вычислить
- 40. Решение.Так как то применима теорема о пределе частного. Значит,
- 41. Пример. Вычислить
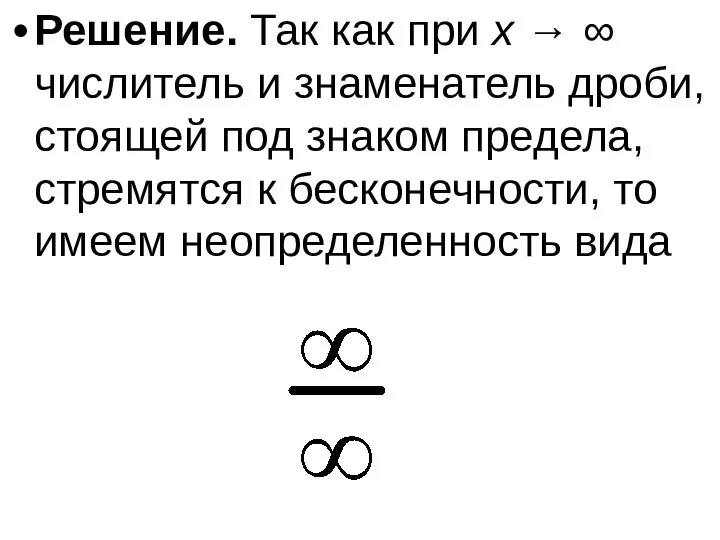
- 42. Решение. Так как при x → ∞ числитель и знаменатель дроби, стоящей под знаком предела, стремятся
- 43. Для раскрытия таких неопределенностей делят числитель и знаменатель дроби на старшую степень x. После деления на
- 45. Пример. Вычислить
- 46. Решение. Так как то имеем неопределённость вида
- 47. Так как, то
- 48. Пример. Вычислить
- 49. Решение. Имеем неопределенность вида Умножим числитель и знаменатель дроби на выражение ( ), а также разложим
- 52. Пример. Вычислить
- 53. Решение. Для раскрытия неопределённости воспользуемся первым замечательным пределом. Считая, что x ≠ 0, проведём очевидные преобразования:
- 55. Пример. Вычислить
- 56. Решение. Для раскрытия неопределённости 1∞ воспользуемся вторым замечательным пределом:
- 57. поскольку
- 58. Сравнение бесконечно малых функций Для сравнения двух бесконечно малых функций α(x) и β(x) в точке x
- 59. Если A ≠ 0 и A ≠ ∞, то функции α(x) и β(x) называются бесконечно малыми
- 60. Если A = 1, то бесконечно малые функции α(x) и β(x) называют эквивалентными и обозначают α(x)
- 61. Основные эквивалентности при x → 0: sin kx ~ kx, tg kx ~ kx, arcsin kx
- 62. При вычислении пределов используют следующую теорему. Теорема. Предел отношения двух бесконечно малых функций в некоторой точке
- 63. Пример. Вычислить
- 64. Решение. Воспользуемся эквивалентными бесконечно малыми функциями. Так как при x → 0 и sin 3x ~
- 66. Сравнение бесконечно малых функций Для сравнения двух бесконечно малых функций α(x) и β(x) в точке x
- 67. Если A ≠ 0 и A ≠ ∞, то функции α(x) и β(x) называются бесконечно малыми
- 68. Если A = 1, то бесконечно малые функции α(x) и β(x) называют эквивалентными и обозначают α(x)
- 69. Основные эквивалентности при x → 0: sin kx ~ kx, tg kx ~ kx, arcsin kx
- 70. При вычислении пределов используют следующую теорему. Теорема. Предел отношения двух бесконечно малых функций в некоторой точке
- 71. Пример. Вычислить
- 72. Решение. Воспользуемся эквивалентными бесконечно малыми функциями. Так как при x → 0 и sin 3x ~
- 74. Непрерывность функции Определение. Функция y = f(x) называется непрерывной в точке x = x0, если предел
- 75. Односторонними называются пределы: левосторонний предел в точке a: правосторонний предел в точке a:
- 76. Определение. Функция y = f(x) называется непрерывной в точке x = x0, если существуют односторонние пределы
- 77. Если односторонние пределы конечны, но нарушается хотя бы одно из равенств то x0 называется точкой разрыва
- 78. Если хотя бы один из этих односторонних пределов не существует или равен бесконечности, то x0 называется
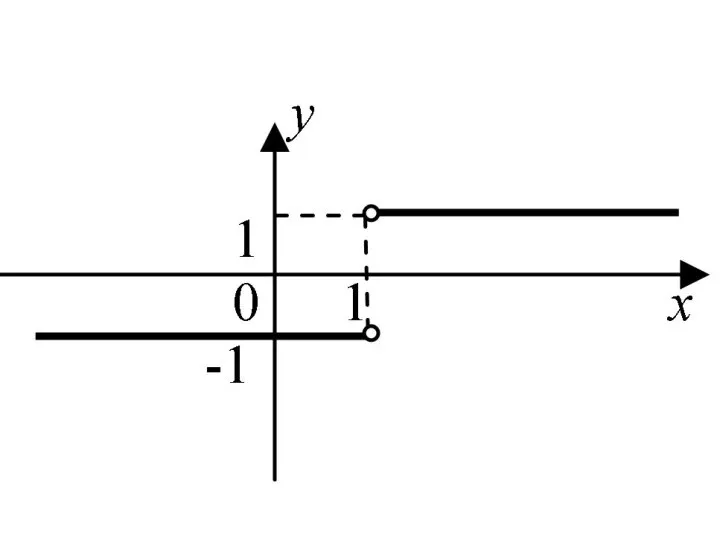
- 79. Например, функция имеет в точке x = 1 разрыв 1-го рода
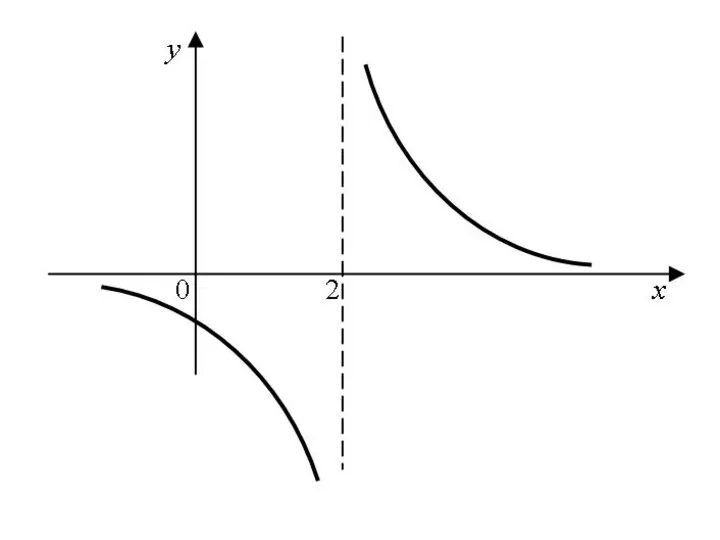
- 81. Функция имеет в точке x = 2 разрыв второго рода
- 83. Если функция непрерывна во всех точках отрезка [a; b], то она называется непрерывной на этом отрезке.
- 84. Из определения непрерывности функции и теорем о пределах следуют теоремы: I. Если функции f(x) и g(x)
- 86. Скачать презентацию












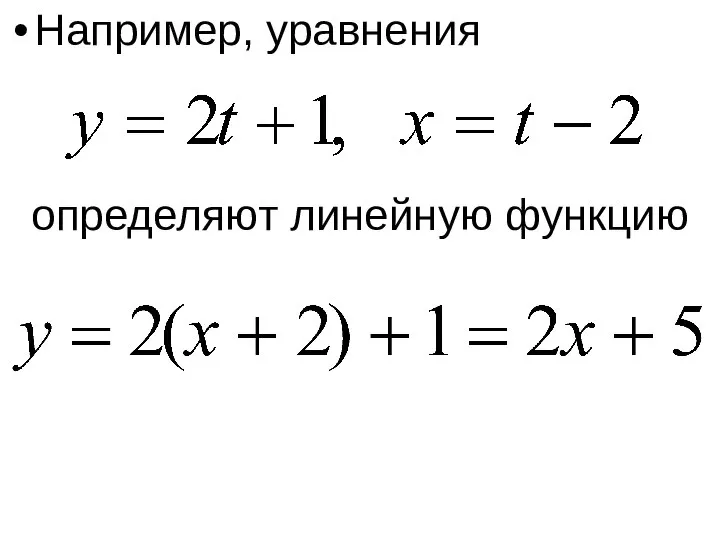


















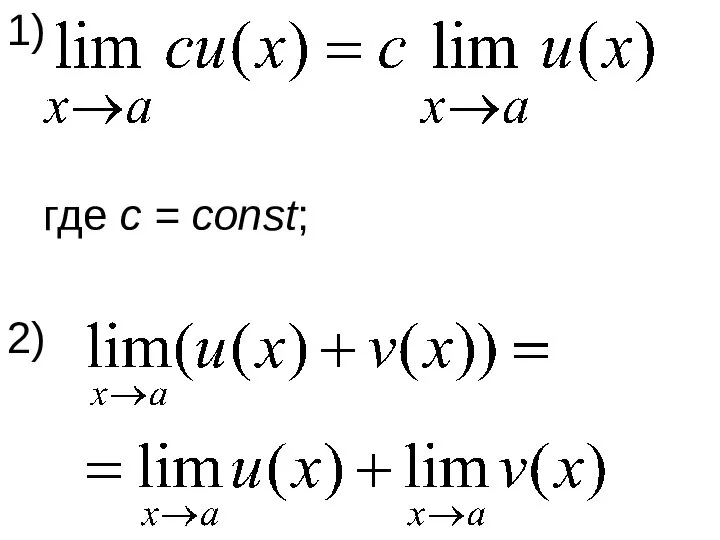
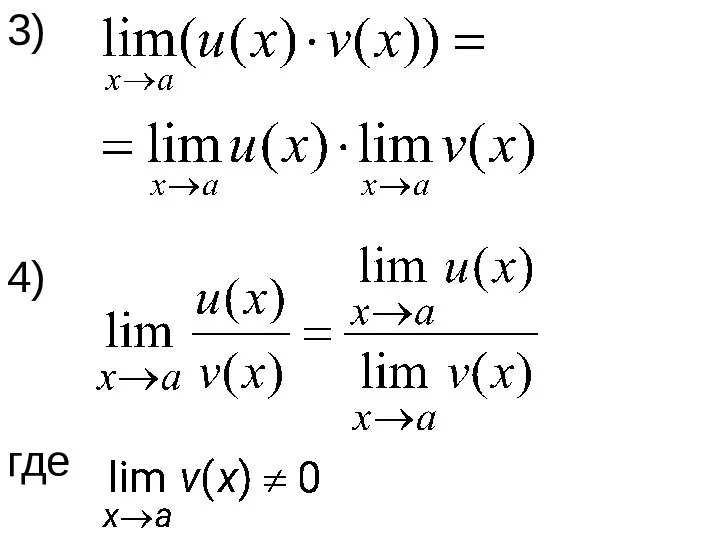
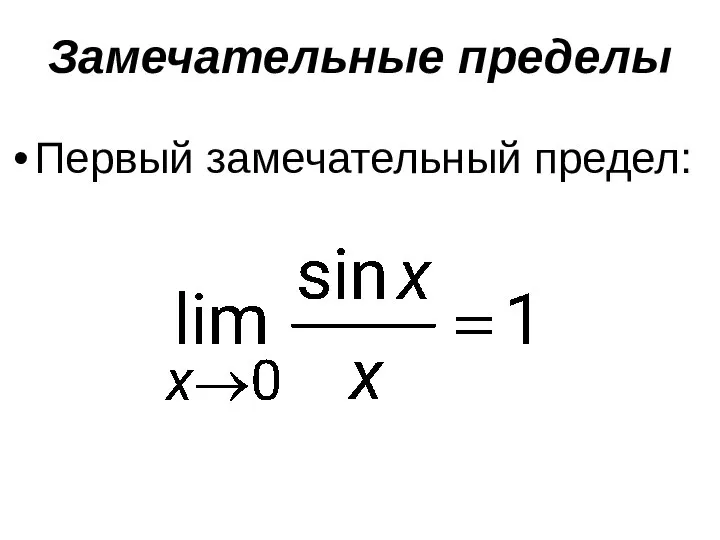


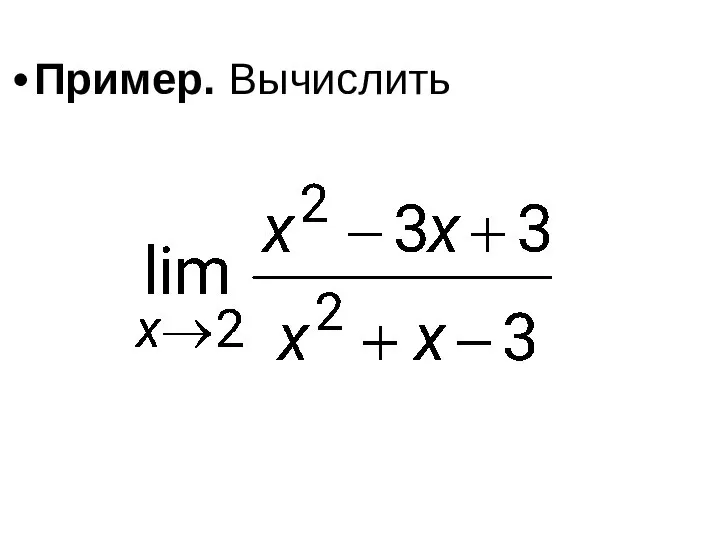

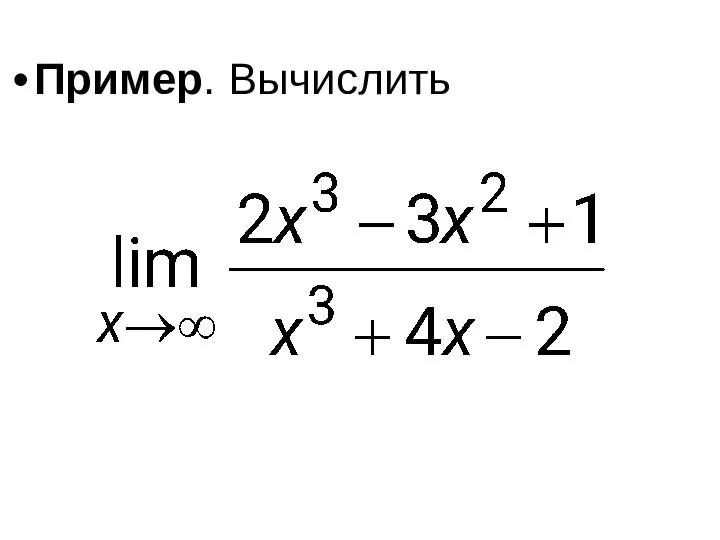

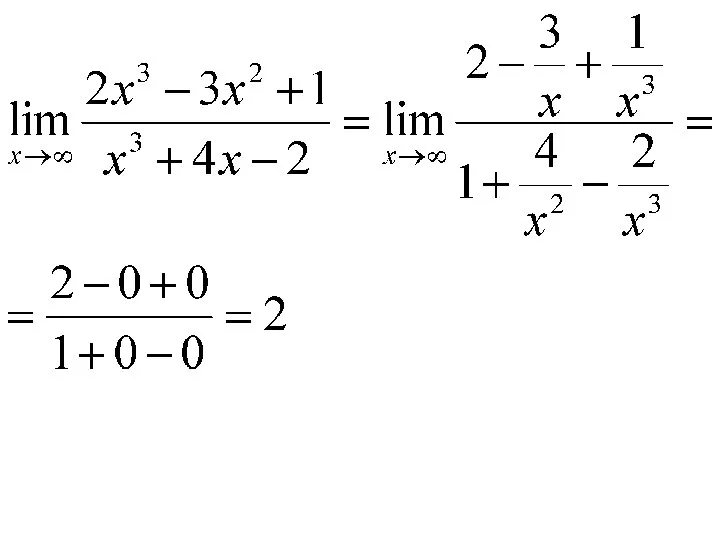
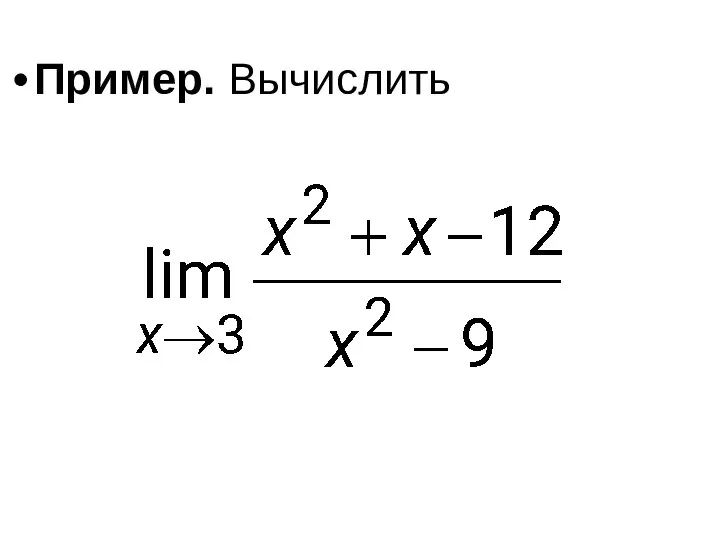
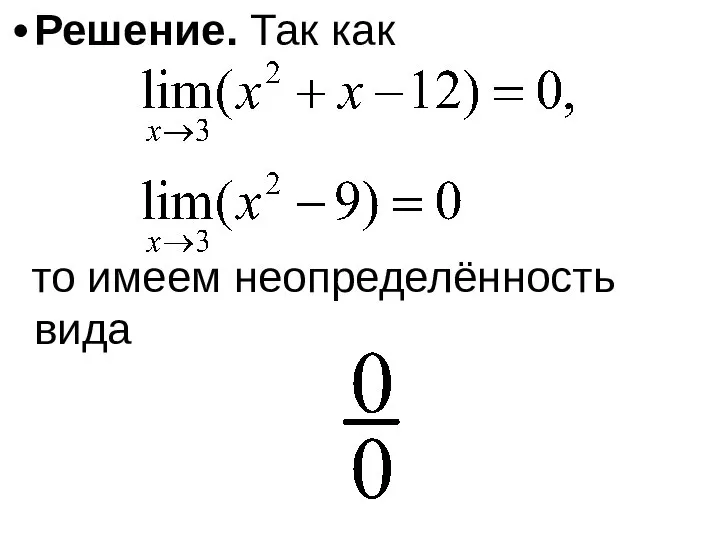
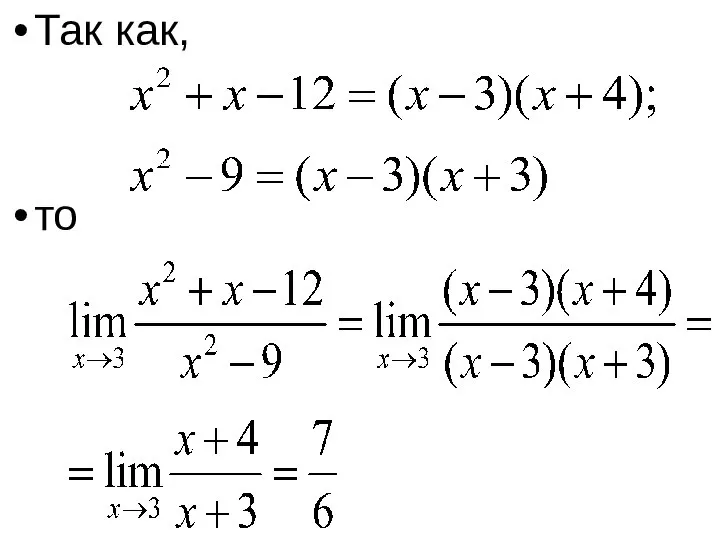
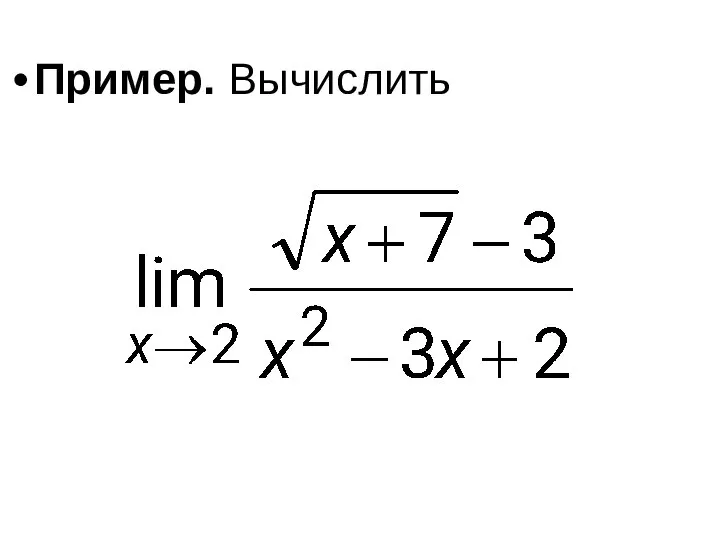

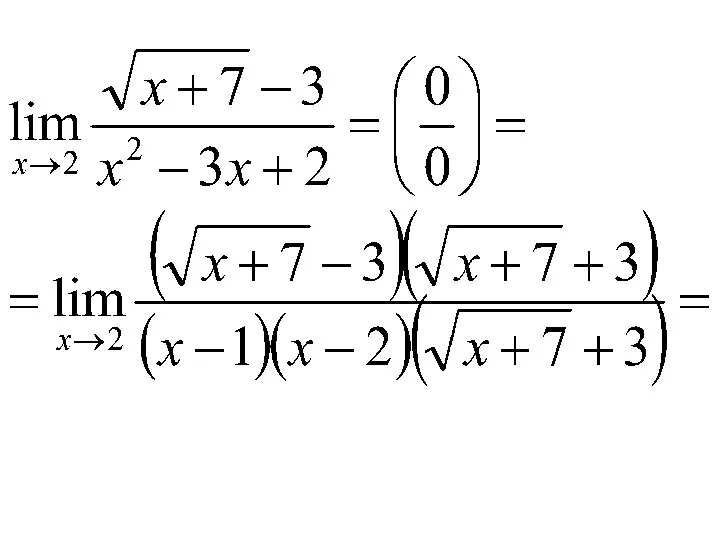
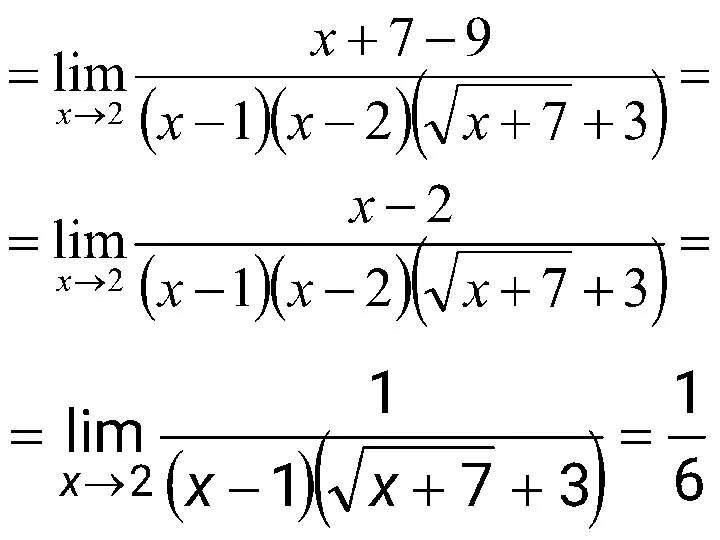
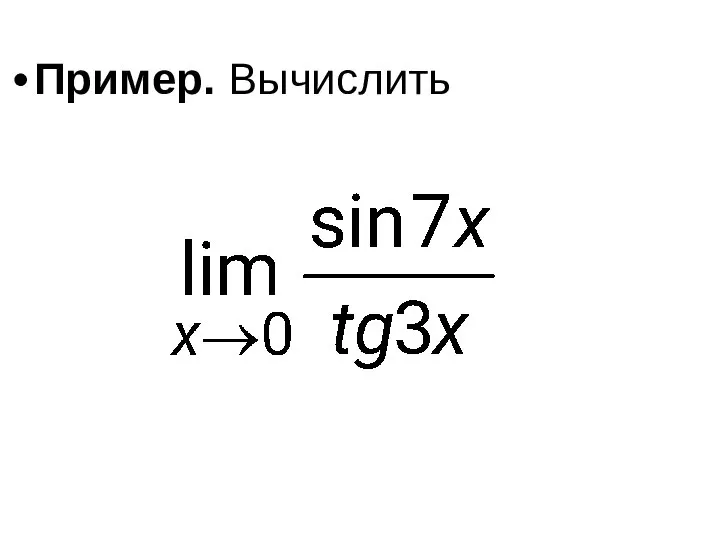

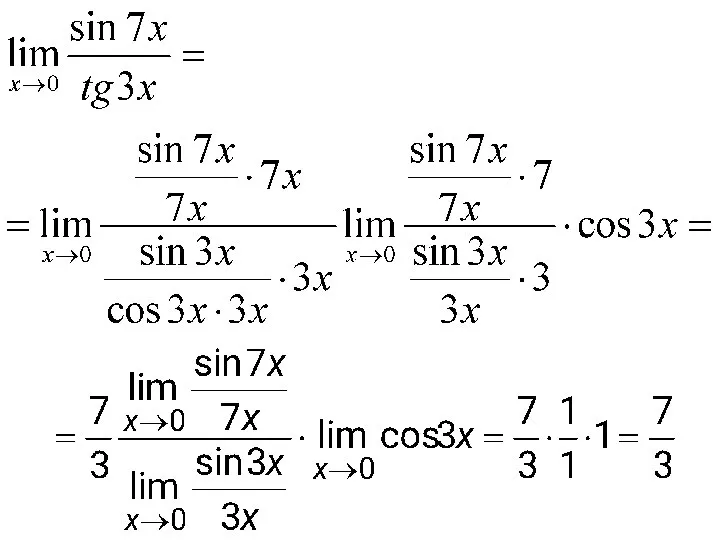
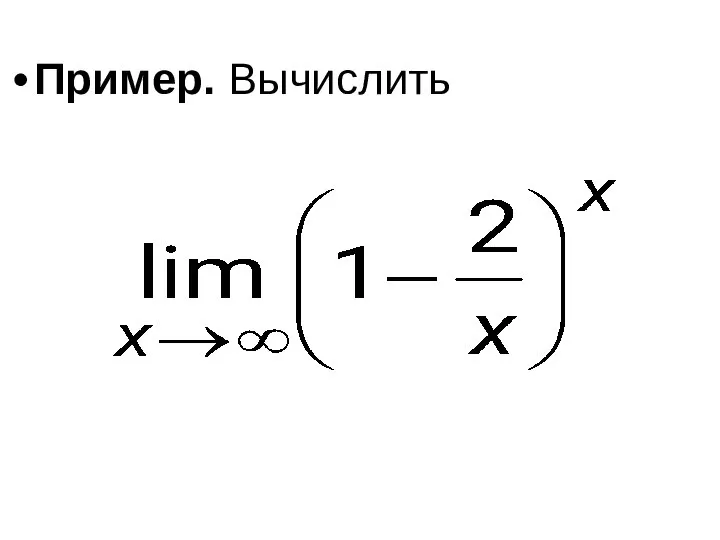

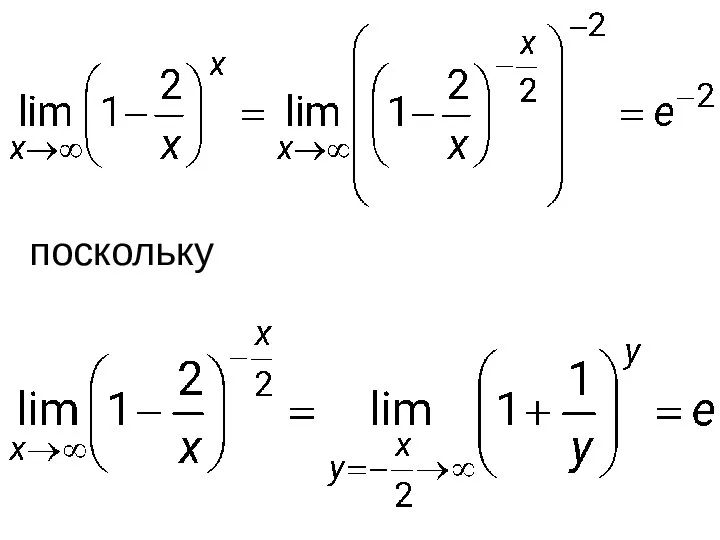





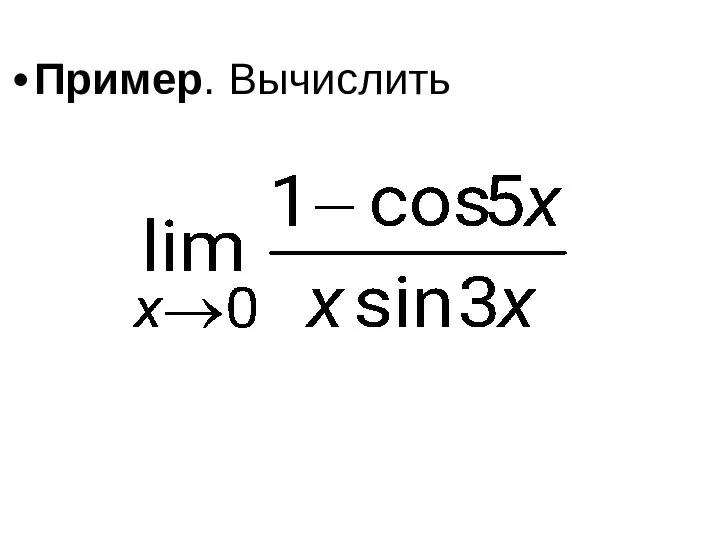

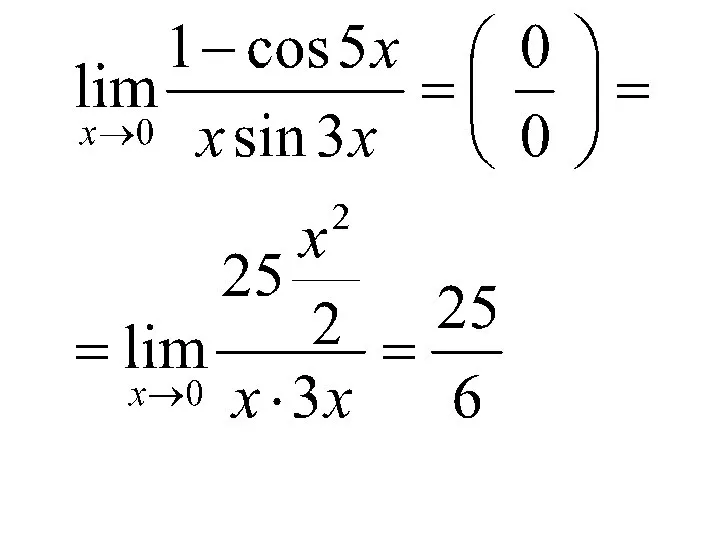


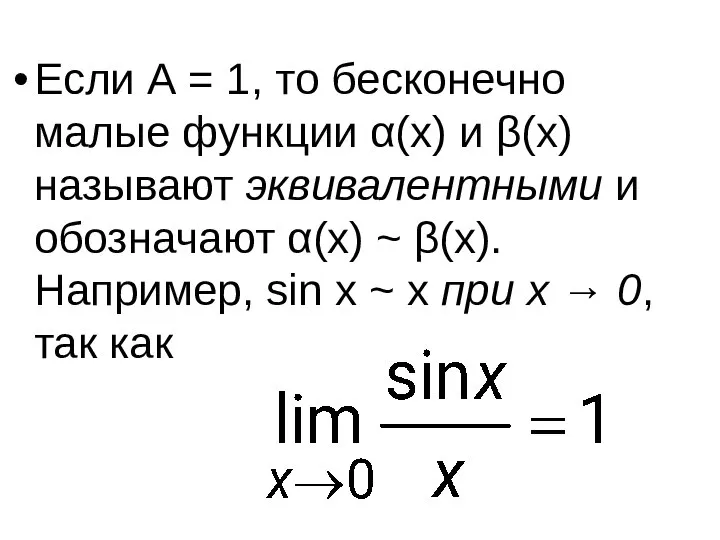


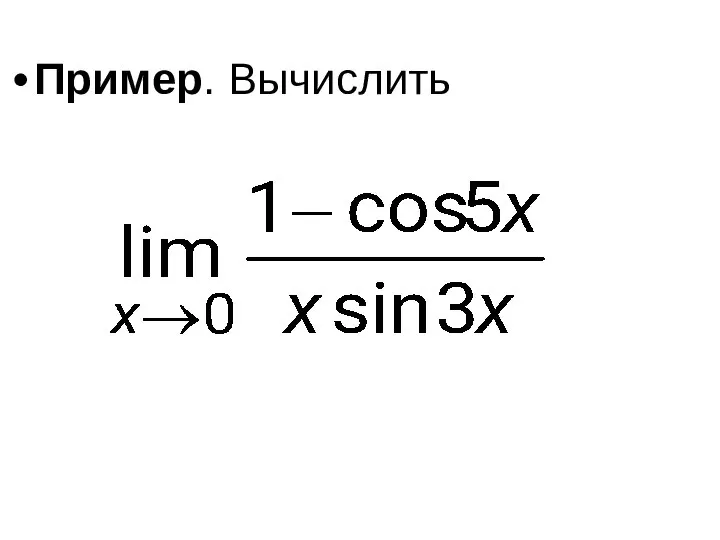

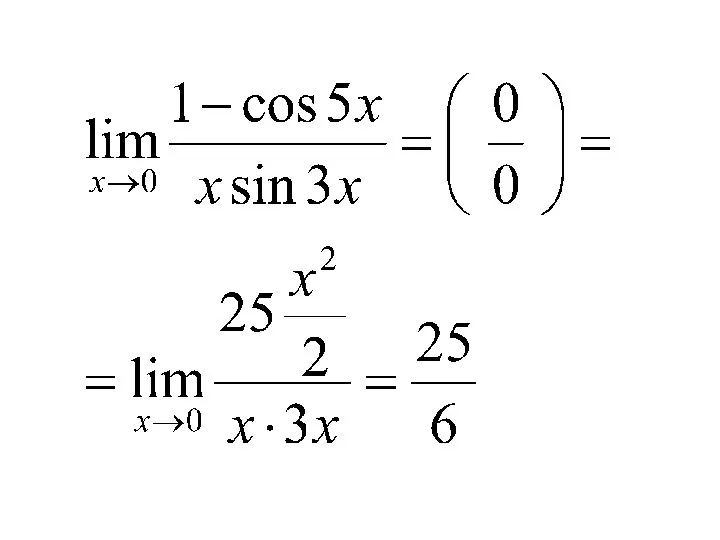







![Если функция непрерывна во всех точках отрезка [a; b], то она называется непрерывной на этом отрезке.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1466297/slide-82.jpg)

 Моделирование выборочных данных суммой экспоненциальных функций Лекция 12
Моделирование выборочных данных суммой экспоненциальных функций Лекция 12 Основные тригонометрические формулы
Основные тригонометрические формулы Свойства функции. Практическое занятие №20
Свойства функции. Практическое занятие №20 Структурные схемы и их преобразование. Типовые динамические звенья САУ и их классификация
Структурные схемы и их преобразование. Типовые динамические звенья САУ и их классификация Сравнение, сложение и вычитание дробей с разными знаменателями и смешанных чисел.
Сравнение, сложение и вычитание дробей с разными знаменателями и смешанных чисел.  Инструменты для вычислений и измерений. 5 класс
Инструменты для вычислений и измерений. 5 класс Двугранный угол
Двугранный угол Умножение и деление алгебраических дробей
Умножение и деление алгебраических дробей Квадратное уравнение
Квадратное уравнение Пропорции. Члены пропорции. Основное свойство пропорции
Пропорции. Члены пропорции. Основное свойство пропорции Теорема Пифагора
Теорема Пифагора Кроссворд по геометрии, 7 класс
Кроссворд по геометрии, 7 класс Работа с одаренными детьми во внеклассной работе по математике в 5-6 классах
Работа с одаренными детьми во внеклассной работе по математике в 5-6 классах Свойства параллельных плоскостей
Свойства параллельных плоскостей Правила и законы математики
Правила и законы математики Обобщение по теме "Четырехугольники". 8 класс
Обобщение по теме "Четырехугольники". 8 класс Класи потоків викликів
Класи потоків викликів Неравенства с двумя переменными
Неравенства с двумя переменными Аттестационная работа. Методическая разработка по выполнению исследовательской работы «Математика оригами»
Аттестационная работа. Методическая разработка по выполнению исследовательской работы «Математика оригами» Свойства числовых функций
Свойства числовых функций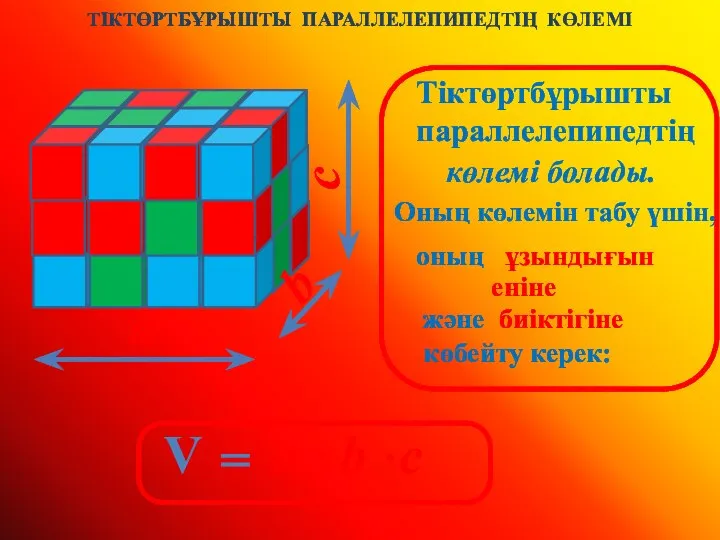 Тіктөртбұрышты параллелепипедтің көлемі
Тіктөртбұрышты параллелепипедтің көлемі Квадрат и куб числа. Тест
Квадрат и куб числа. Тест Симетрія відносно прямої (осьова симетрія)
Симетрія відносно прямої (осьова симетрія) Алгоритмическая разрешимость. Алгоритмически неразрешимые задачи
Алгоритмическая разрешимость. Алгоритмически неразрешимые задачи Конус как тело вращения
Конус как тело вращения Математика в средней группе. Цифра 6
Математика в средней группе. Цифра 6 Геометрический смысл производной
Геометрический смысл производной НЕРАВЕНСТВА (8 КЛАСС)
НЕРАВЕНСТВА (8 КЛАСС)