Содержание
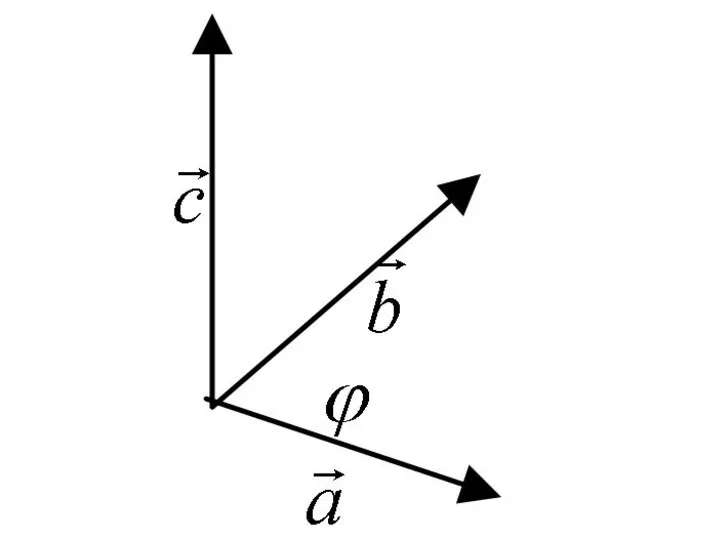
- 2. 1. 2. 3. тройка – правая (т.е. при наблюдении из конца вектора кратчайший поворот от к
- 4. Свойства векторного произведения 1. 2. 3. 4.
- 5. Если то векторное произведение вычисляется по формуле
- 6. Приложения векторного произведения к задачам геометрии и механики.
- 7. Площадь параллелограмма (геометрический смысл векторного произведения). Площадь треугольника
- 8. Момент силы (механический смысл векторного произведения). Пусть точка А твердого тела закреплена, а в точке В
- 9. Пример. Вычислить площадь треугольника с вершинами A(7,3,4), B(1,0,6) , C(4,5,-2).
- 10. Решение. Находим векторы Вычисляем векторное произведение
- 12. Тогда
- 13. Смешанное произведение векторов Определение. Смешанным произведением трех векторов называется число
- 14. Если то
- 15. Приложения смешанного произведения к задачам геометрии
- 16. Объём параллелепипеда, построенного на векторах (геометрический смысл смешанного произведения). Объём пирамиды
- 17. Условие компланарности векторов в координатной форме: – компланарны
- 18. Пример. Вычислить объём пирамиды с вершинами в точках A(2,0,0), B(0,3,0), C(4,0,6), D(2,3,8).
- 19. Решение. Находим векторы Вычислим смешанное произведение этих векторов:
- 21. Тогда
- 23. Модуль 2 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
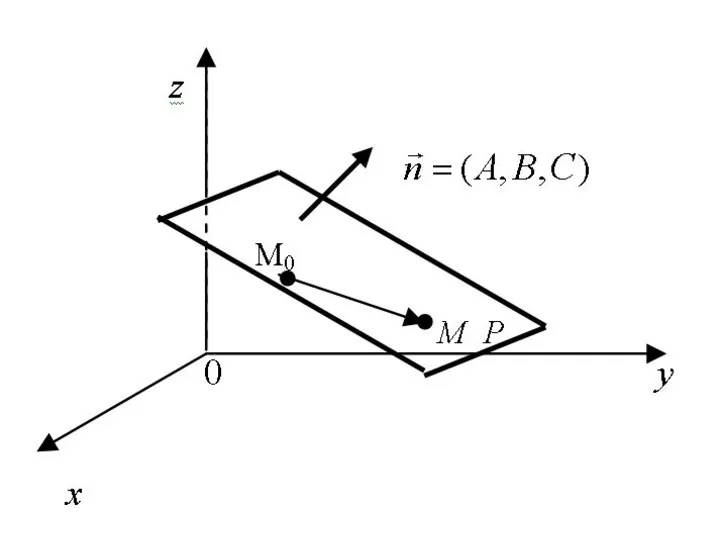
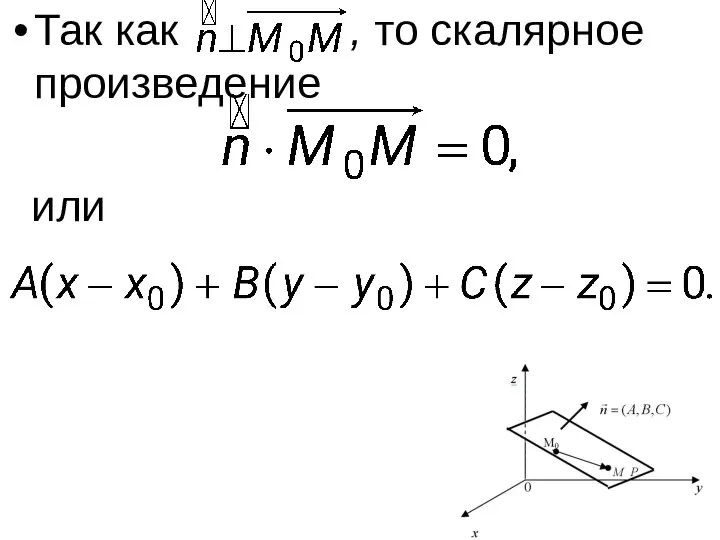
- 24. Плоскость и её основные уравнения Рассмотрим плоскость P в прямоугольной декартовой системе координат.
- 25. Положение плоскости вполне определяется точкой и вектором нормали
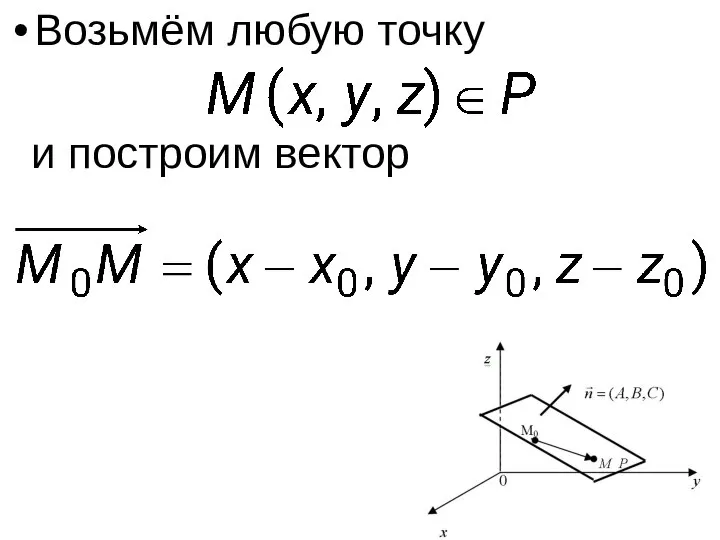
- 27. Возьмём любую точку и построим вектор
- 28. Так как , то скалярное произведение или
- 29. Получили уравнение плоскости, заданной точкой и вектором нормали
- 30. Если в уравнении раскрыть скобки и обозначить то получим общее уравнение плоскости:
- 31. Теорема. Всякое уравнение вида определяет некоторую плоскость в пространстве.
- 32. Если в этом уравнении какой-либо из коэффициентов A, B, C равен нулю, то плоскость расположена параллельно
- 33. Например, при A = 0 плоскость By + Cz + D = 0 параллельна оси Ox;
- 34. Пусть в уравнении ни один из коэффициентов не равен 0. Перепишем это уравнение в виде разделим
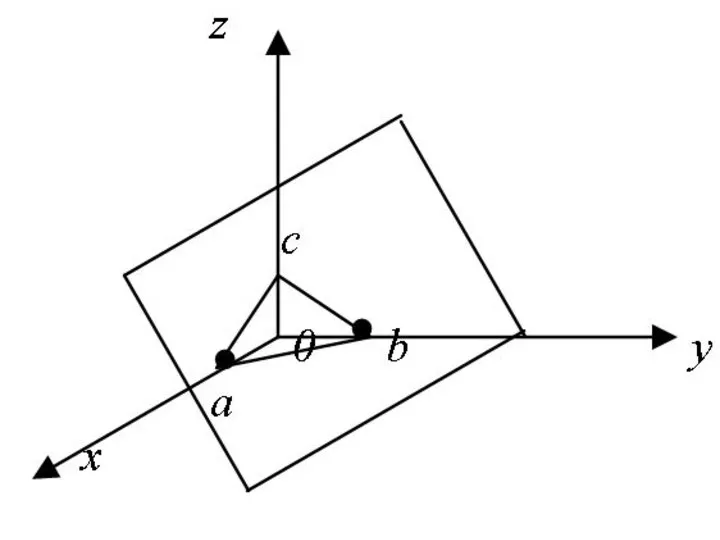
- 35. Получим уравнение плоскости в отрезках:
- 36. где a, b, c – это величины направленных отрезков, отсекаемых плоскостью на осях координат
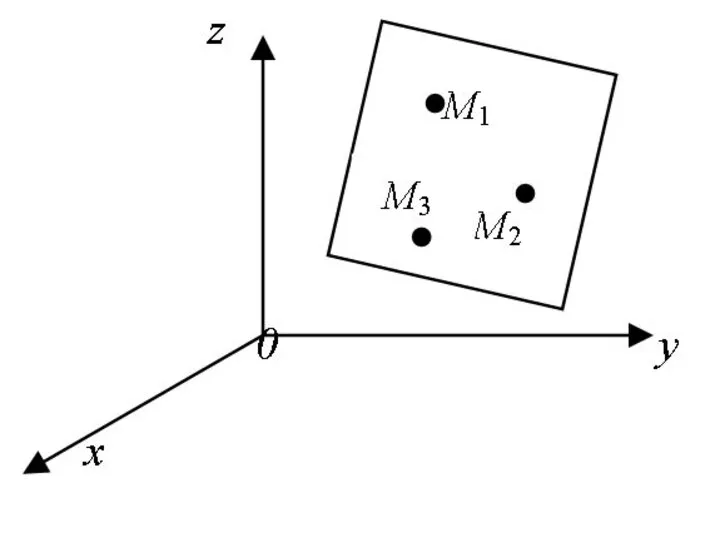
- 38. Если три точки не лежат на одной прямой, то через эти точки проходит единственная плоскость:
- 40. Уравнение плоскости, проходящей через три точки, имеет вид:
- 41. Пусть даны две плоскости и Угол φ между двумя плоскостями равен углу между их векторами нормали:
- 43. Расстояние d от точки до плоскости определяется по формуле
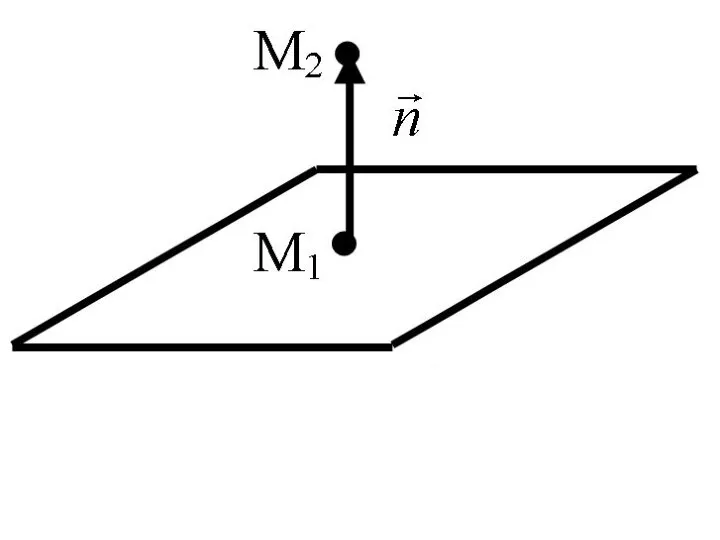
- 44. Пример. Даны две точки Записать уравнение плоскости, проходящей через точку M1 перпендикулярно вектору
- 45. Решение. Поскольку искомая плоскость перпендикулярна вектору , то в качестве вектора нормали возьмем вектор
- 47. Подставив теперь в уравнение а также координаты точки M1: получим уравнение
- 49. Скачать презентацию








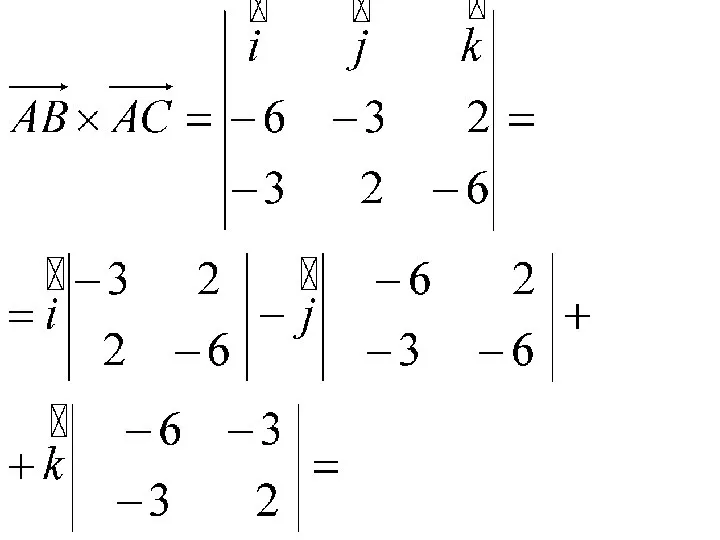
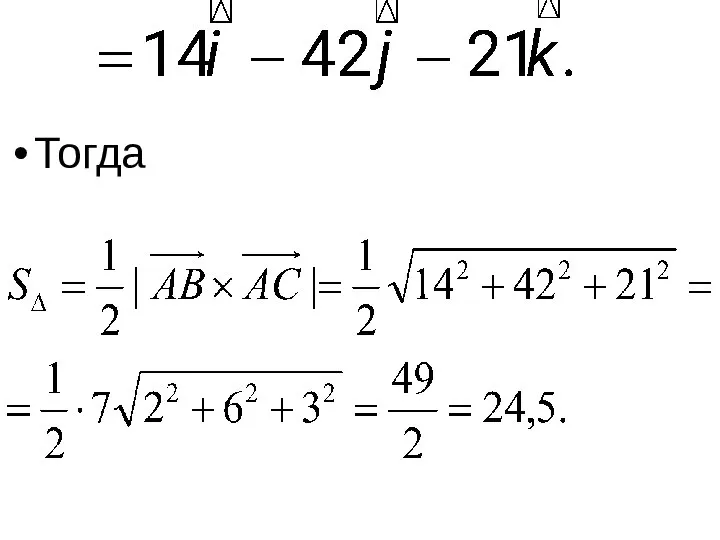

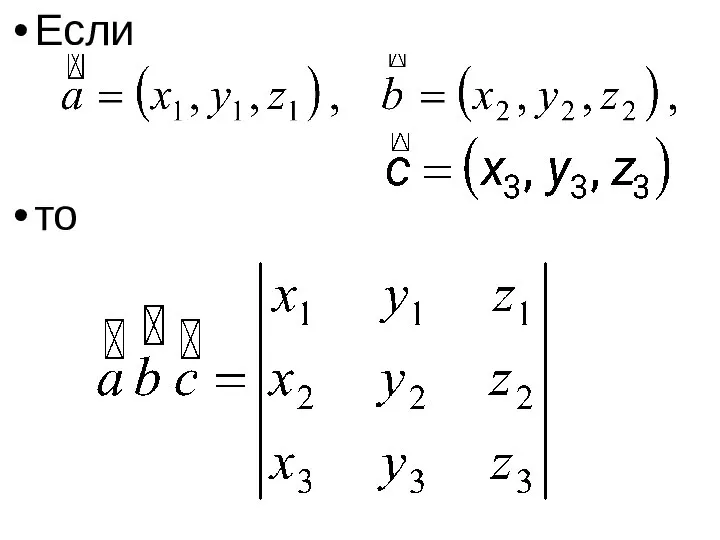





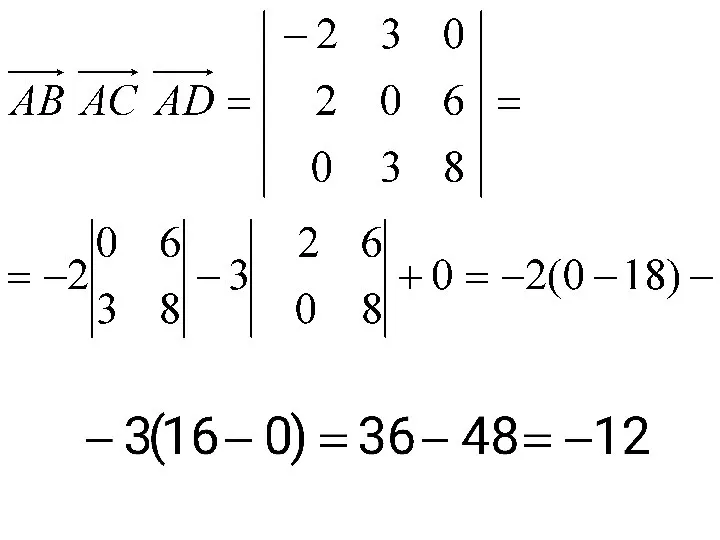
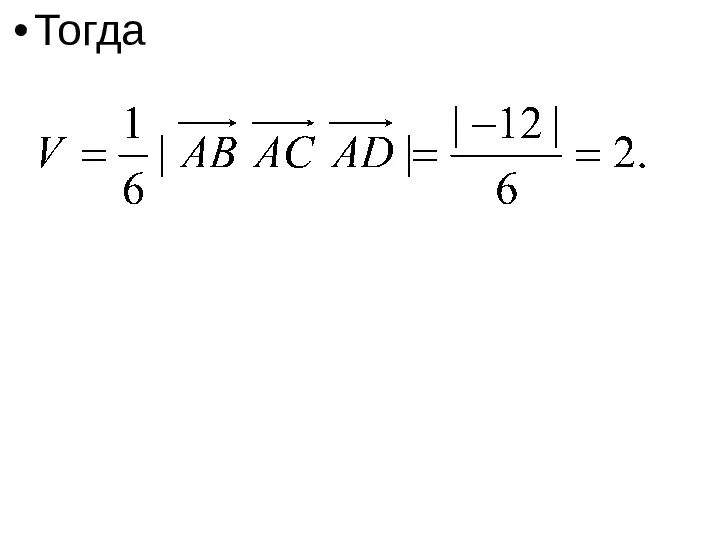















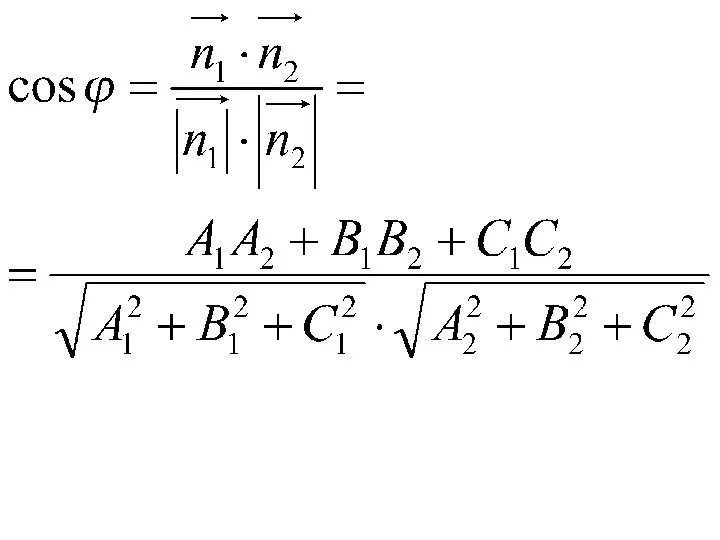




 Параллель к перпендикуляру
Параллель к перпендикуляру Презентация на тему Аксиомы стереометрии
Презентация на тему Аксиомы стереометрии  Презентация на тему Решение задач 1 класс
Презентация на тему Решение задач 1 класс  УМК по предмету «Счёт и конструирование» и дидактический материал по данной теме, для подготовительного класса
УМК по предмету «Счёт и конструирование» и дидактический материал по данной теме, для подготовительного класса Непрерывность функций Лекция 3
Непрерывность функций Лекция 3  Четырёхугольники (повторение материала)
Четырёхугольники (повторение материала) Интерполяционные формулы Гаусса, Стирлинга, Бесселя
Интерполяционные формулы Гаусса, Стирлинга, Бесселя Метод координат
Метод координат Презентация по математике "Расположение точек относительно осей координат" - скачать бесплатно
Презентация по математике "Расположение точек относительно осей координат" - скачать бесплатно Сечение сферы плоскостями уровня. Сечение шара проецирующими плоскостями
Сечение сферы плоскостями уровня. Сечение шара проецирующими плоскостями Ֆունկցիայի գրաֆիկի ձևափոխություններ
Ֆունկցիայի գրաֆիկի ձևափոխություններ Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Дифференциальные уравнения
Дифференциальные уравнения Презентация по математике "Обыкновенные дроби" - скачать
Презентация по математике "Обыкновенные дроби" - скачать  Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки. Сумма двух векторов
Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки. Сумма двух векторов Применение производной при решении физических задач» (11 класс)
Применение производной при решении физических задач» (11 класс) Решение простейших тригонометрических неравенств
Решение простейших тригонометрических неравенств Координатная плоскость
Координатная плоскость Интегральный признак Коши. (Лекция 2.16)
Интегральный признак Коши. (Лекция 2.16) Интерполяция. Графический способ интерполяции
Интерполяция. Графический способ интерполяции Сводка и группировка статистических даных. (Лекция 3)
Сводка и группировка статистических даных. (Лекция 3) Равнобедренный треугольник
Равнобедренный треугольник О, математики! Игра
О, математики! Игра Презентация на тему Число 9
Презентация на тему Число 9 Комбинаторика
Комбинаторика Последовательности
Последовательности Презентация по математике "Двузначные числа" - скачать
Презентация по математике "Двузначные числа" - скачать  Действия над обыкновенными дробями. Счет и вычисления
Действия над обыкновенными дробями. Счет и вычисления