Вычисление интегралов различными методами

Июль 25, 2022

Главная
Математика
Вычисление интегралов различными методами

Содержание

2. Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b) (конечном или бесконечном), если в каждой
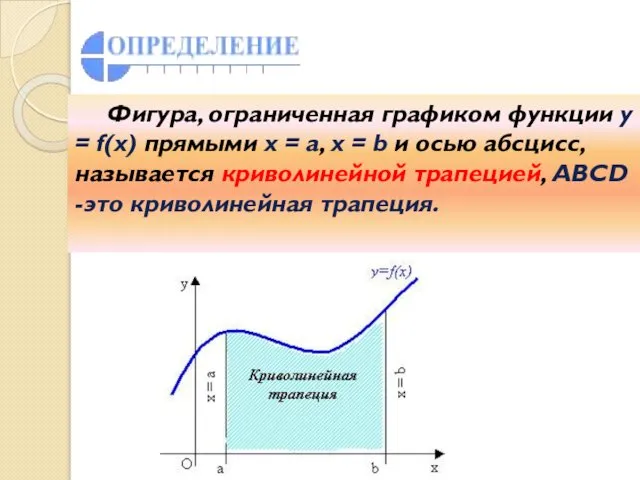
3. Фигура, ограниченная графиком функции y = f(x) прямыми x = a, x = b и осью
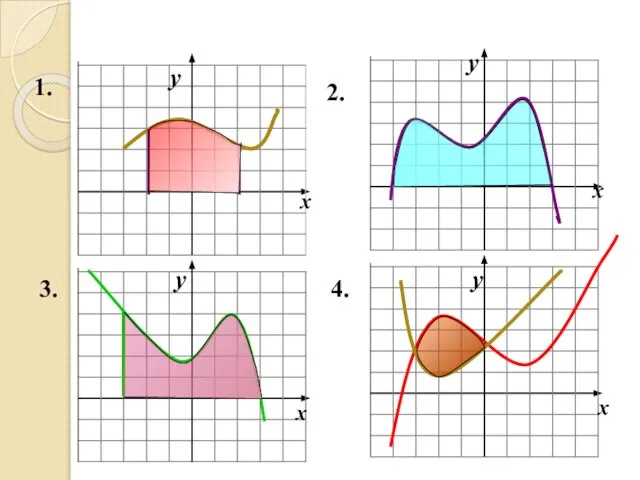
4. y y y y x x x x 1. 4. 3. 2.
6. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
7. ФОРМУЛА НЬЮТОНА- ЛЕЙБНИЦА Если f(х) – непрерывная и неотрицательная на отрезке [a; b] функция , а
8. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
10. Таблица интегралов
11. Примеры:
12. Пример Вычислить .
13. Интегрирование методом подстановки.
15. Пример
16. Интегрирование по частям
18. Пример
19. Применение определенного интеграла для вычисления площадей плоских фигур
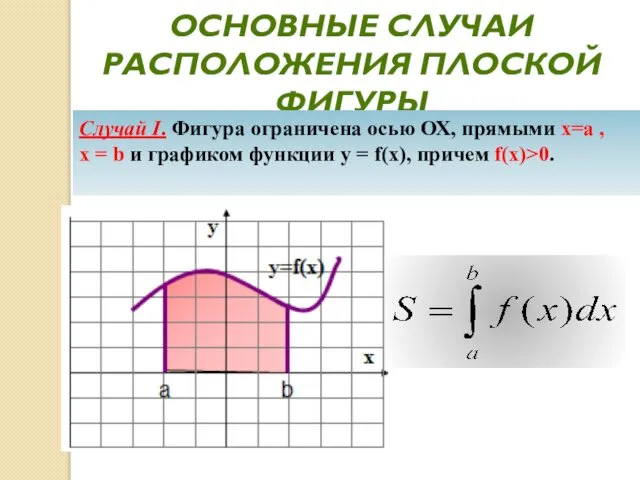
20. ОСНОВНЫЕ СЛУЧАИ РАСПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ Случай I. Фигура ограничена осью ОХ, прямыми х=а , х =
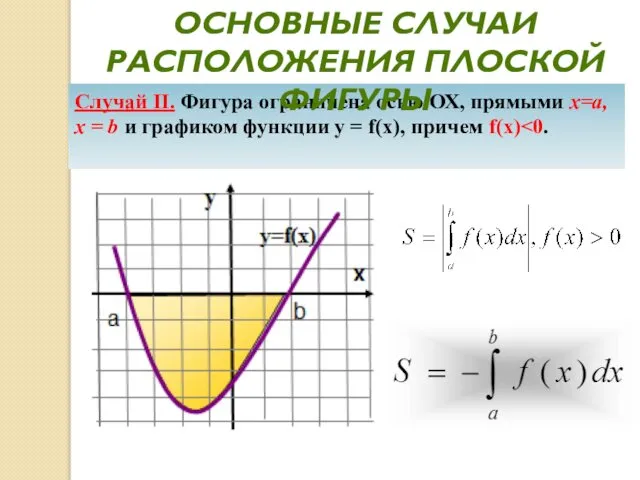
21. Случай II. Фигура ограничена осью ОХ, прямыми х=а, х = b и графиком функции у =
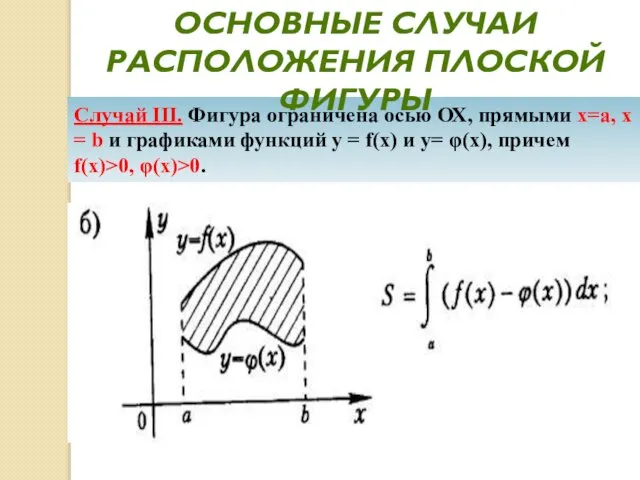
22. Случай III. Фигура ограничена осью ОХ, прямыми х=а, х = b и графиками функций у =
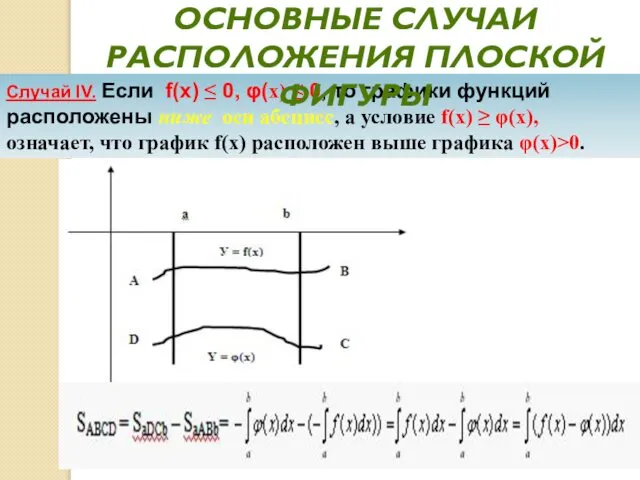
23. Случай IV. Если f(x) ≤ 0, φ(x) ≤ 0, то графики функций расположены ниже оси абсцисс,
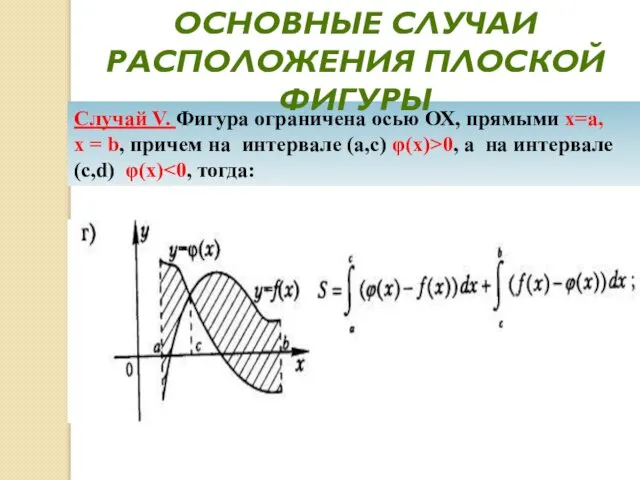
24. Случай V. Фигура ограничена осью ОХ, прямыми х=а, х = b, причем на интервале (а,с) φ(x)>0,
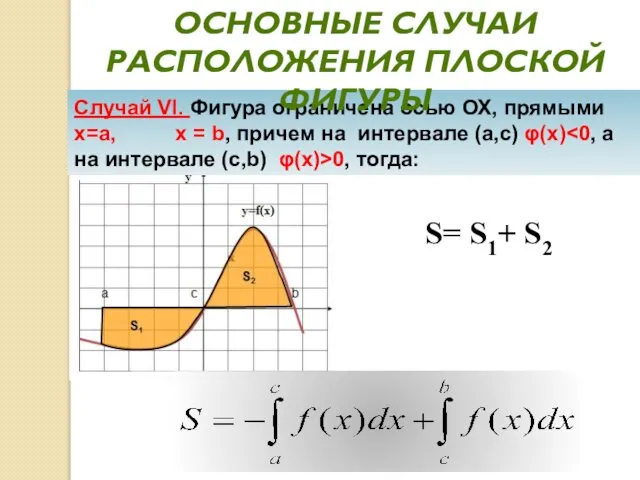
25. Случай VI. Фигура ограничена осью ОХ, прямыми х=а, х = b, причем на интервале (а,с) φ(x)
26. Сделать чертеж графиков заданных функций, ограничивающих площадь плоских фигур. Найти пределы интегрирования. Выяснить какой формулой площади
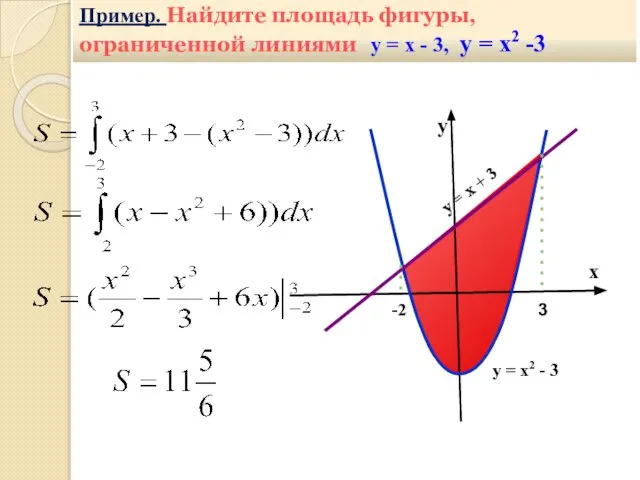
27. х у = х2 - 3 Пример. Найдите площадь фигуры, ограниченной линиями у = х -
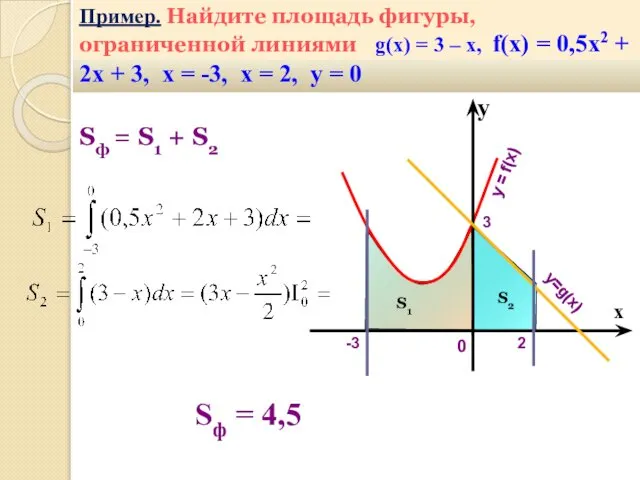
28. Пример. Найдите площадь фигуры, ограниченной линиями g(x) = 3 – х, f(x) = 0,5х2 + 2х
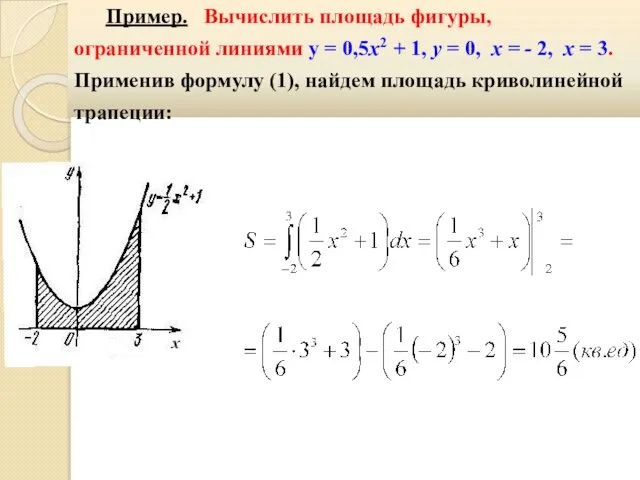
29. Пример. Вычислить площадь фигуры, ограниченной линиями y = 0,5х2 + 1, y = 0, х =
30. Пример. Вычислить площадь фигуры, ограниченной линиями y = - х2 - 1, у = 0, х
31. Пример . Вычислить площадь фигуры, ограниченной линиями у = sin х, y = 0, х =
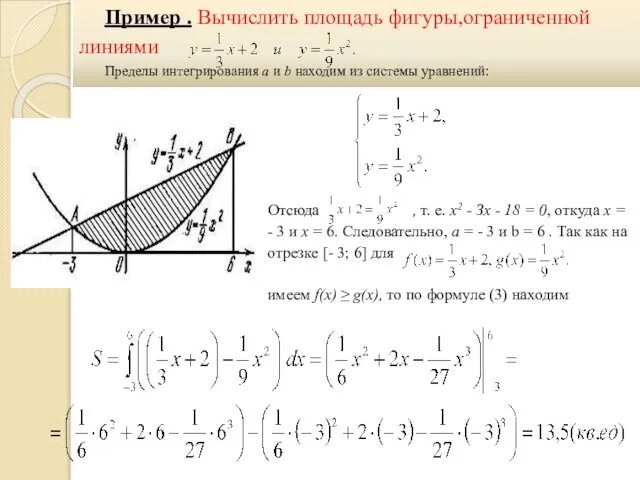
32. Пример . Вычислить площадь фигуры,ограниченной линиями Пределы интегрирования а и b находим из системы уравнений: Отсюда
33. Вычислить площадь фигур, ограниченных линиями (работа в группах) у = х2 + 1, у = 5
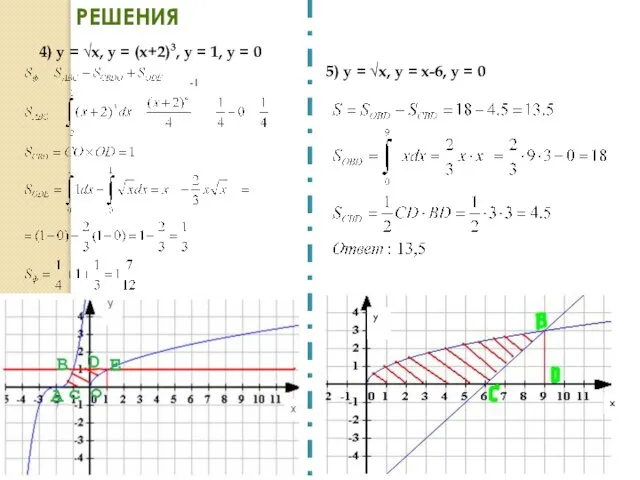
34. РЕШЕНИЯ 4) у = √х, у = (х+2)3, у = 1, у = 0 5) у
35. Итоговый контроль Вычислить площади фигур, ограниченных линиями. у = 5 - х2, у = 3 -
36. Ответы 1 – б 2 – г 3 – в 4 – в Назад к заданиям
37. Самостоятельная работа.
39. Скачать презентацию

Слайд 2

Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b) (конечном

или бесконечном), если в каждой точке этого интервала f(x) является производной для F(x), т.е.

Слайд 3

Фигура, ограниченная графиком функции y = f(x) прямыми x = a,

x = b и осью абсцисс, называется криволинейной трапецией, ABCD -это криволинейная трапеция.

Слайд 4

y
y
y
y
x
x
x
x
1.
4.
3.
2.

Слайд 5

Слайд 6

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Слайд 7

ФОРМУЛА НЬЮТОНА- ЛЕЙБНИЦА
Если f(х) – непрерывная и неотрицательная на отрезке [a;

b] функция , а F(х) – ее первообразная на этом отрезке , то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a; b] , т.е.

Слайд 8

СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Слайд 9

СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Слайд 10

Таблица интегралов

Слайд 11

Примеры:

Слайд 12

Пример
Вычислить .

Слайд 13

Интегрирование методом подстановки.

Слайд 14

Слайд 15

Пример

Слайд 16

Интегрирование по частям

Слайд 17

Слайд 18

Пример

Слайд 19

Применение определенного интеграла для вычисления площадей плоских фигур

Слайд 20

ОСНОВНЫЕ СЛУЧАИ РАСПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
Случай I. Фигура ограничена осью ОХ, прямыми

х=а , х = b и графиком функции у = f(x), причем f(x)>0.

Слайд 21