Содержание
- 2. Площади фигур, расположенных над осью Ох Пусть на отрезке функция f(x) принимает неотрицательные значения, т.е. для
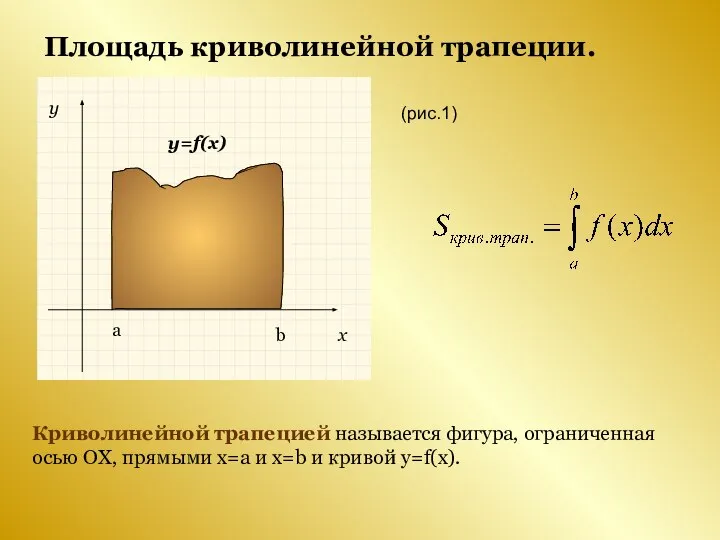
- 3. Площадь криволинейной трапеции. Криволинейной трапецией называется фигура, ограниченная осью ОХ, прямыми х=а и х=b и кривой
- 4. Вычислим площади фигур, ограниченных заданными линиями: Дано: =9x, x=16, x=25 и y=0 Решение: Для любого функция
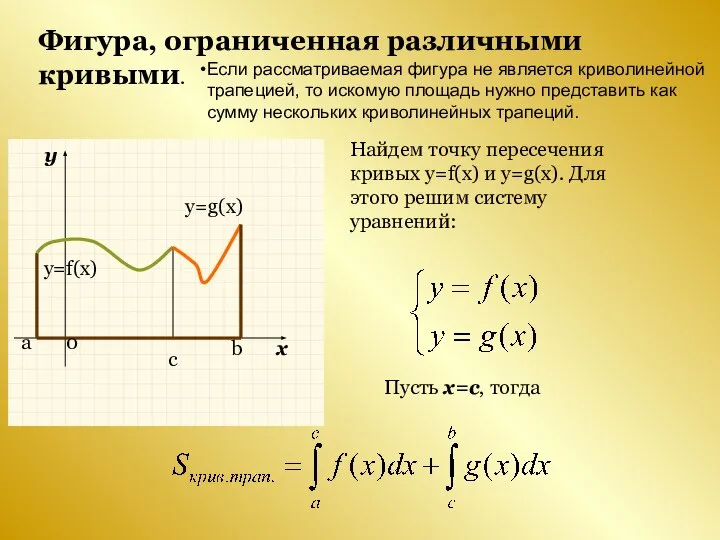
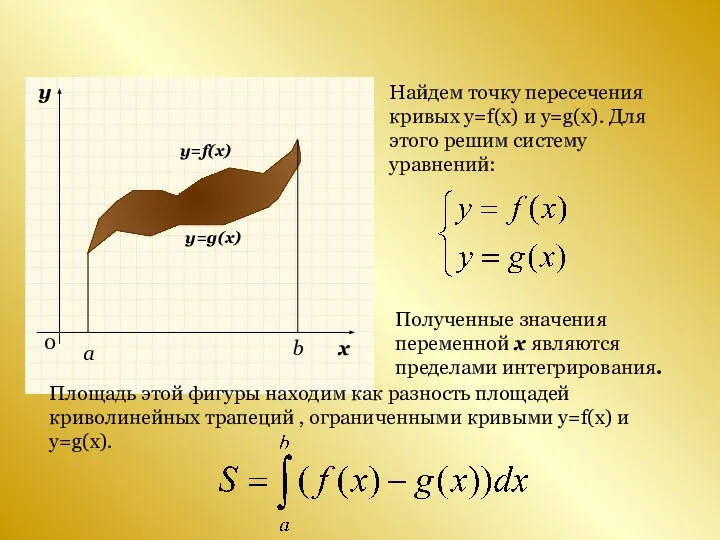
- 5. Фигура, ограниченная различными кривыми. Найдем точку пересечения кривых y=f(x) и y=g(x). Для этого решим систему уравнений:
- 6. y=f(x) y=g(x) a b Найдем точку пересечения кривых y=f(x) и y=g(x). Для этого решим систему уравнений:
- 7. Вычислить площадь фигуры, ограниченной линиями x-2y+4=0, y+x-5=0 и y=0 Решение: 1. Выполним построение фигуры. Построим прямую
- 8. 3. Для треугольника AMN имеем х-2у+4=0; , ; а=-4; b=2. Для треугольника NMC получим х+у-5=0; у=-х+5;
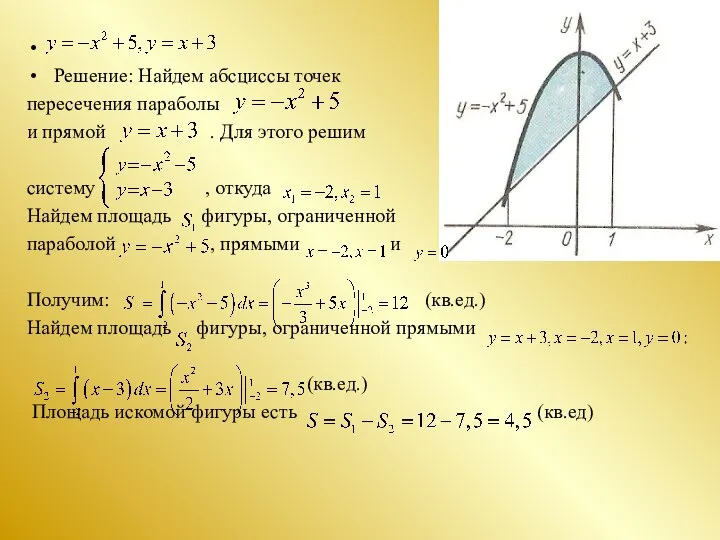
- 9. Решение: Найдем абсциссы точек пересечения параболы и прямой . Для этого решим систему , откуда Найдем
- 10. Вычислить площадь фигуры, ограниченной кривыми Решение: Как видно из рисунка, площадь фигуры ОВАМАО можно представить как
- 11. Данную задачу можно решить и другим способом. Представим искомую площадь в виде разностей площадей фигур ОАМNO
- 12. Площади фигур, расположенных полностью или частично под осью Ох Пусть на отрезке [a,b] задана неположительная непрерывная
- 13. у=-2х, у=0 и х=3 Решение: На отрезке [0,3] функция f(x)=-2x отрицательна; поэтому для вычисления площади искомой
- 14. Решение: Парабола пересекает ось абсцисс в точках х=0 и х=4. Фигура, площадь которой требуется найти, отмечена
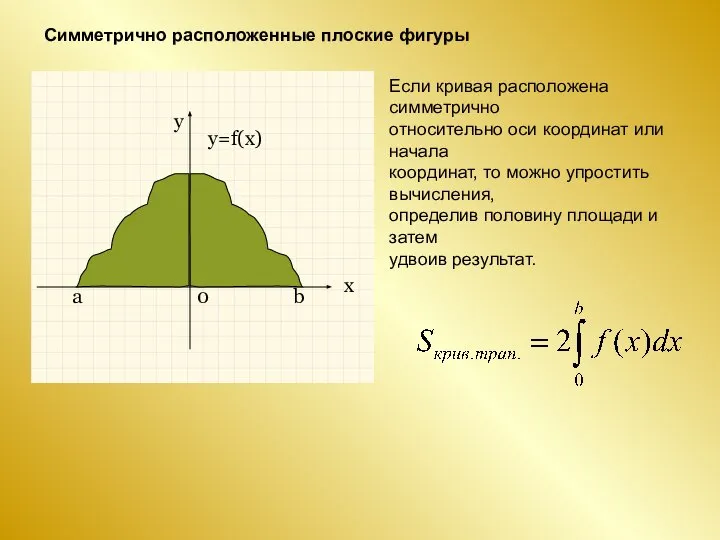
- 15. Симметрично расположенные плоские фигуры Если кривая расположена симметрично относительно оси координат или начала координат, то можно
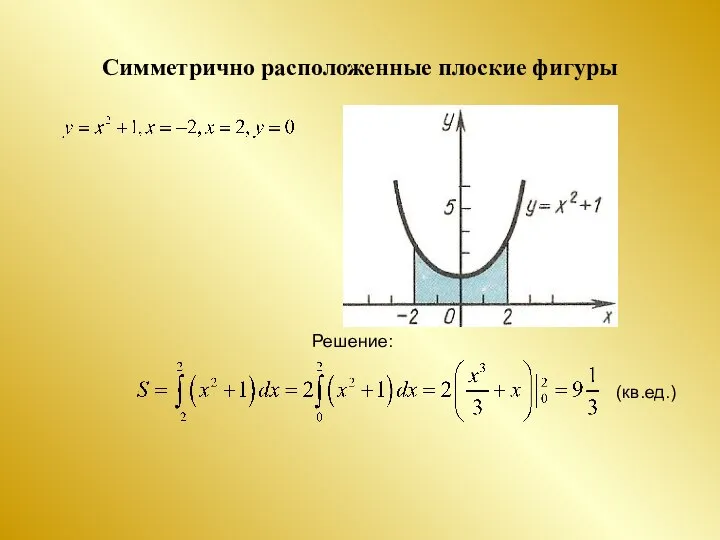
- 16. Симметрично расположенные плоские фигуры Решение: (кв.ед.)
- 17. Если f(x) на отрезке [a,b] меняет знак конечное число раз, то этот отрезок следует разбить на
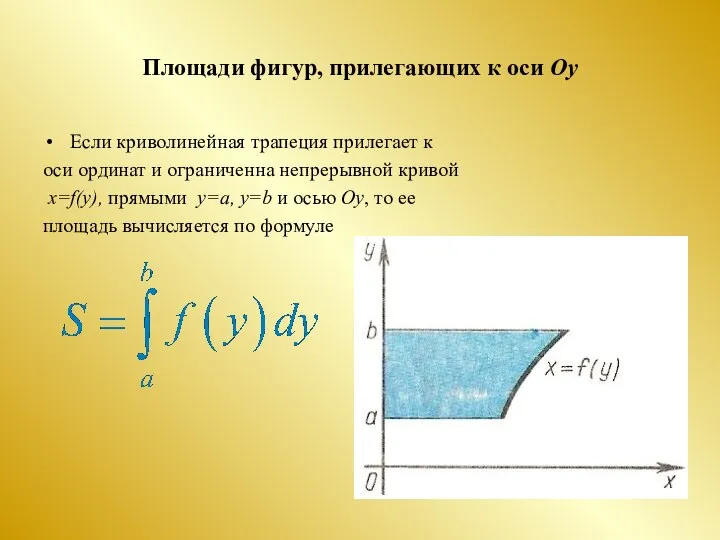
- 18. Площади фигур, прилегающих к оси Оу Если криволинейная трапеция прилегает к оси ординат и ограниченна непрерывной
- 20. Скачать презентацию







![у=-2х, у=0 и х=3 Решение: На отрезке [0,3] функция f(x)=-2x отрицательна;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1490660/slide-12.jpg)

![Если f(x) на отрезке [a,b] меняет знак конечное число раз, то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1490660/slide-16.jpg)
 Сравнение чисел
Сравнение чисел Введение в теорию игр
Введение в теорию игр Фрактальная графика
Фрактальная графика Визначений інтеграл
Визначений інтеграл Луч и угол. (7 класс)
Луч и угол. (7 класс) Задачи на смеси, сплавы, растворы
Задачи на смеси, сплавы, растворы Квадратный корень. Математический диктант
Квадратный корень. Математический диктант Математические ребусы
Математические ребусы Решение уравнений, приводимых к квадратным
Решение уравнений, приводимых к квадратным Десятичная дробь. Графический диктант
Десятичная дробь. Графический диктант Требования к оформлению печатных проектно-исследовательских работ
Требования к оформлению печатных проектно-исследовательских работ Зеркальная симметрия и параллельный перенос
Зеркальная симметрия и параллельный перенос Вынесение общего множителя за скобки
Вынесение общего множителя за скобки Вычисление площади треугольника
Вычисление площади треугольника Время. Решение задач
Время. Решение задач Проверка гипотез. Основы ДА
Проверка гипотез. Основы ДА Correlation and regression
Correlation and regression Координатная плоскость. (6 класс)
Координатная плоскость. (6 класс) Математический тренажёр «Бабушкины примеры»
Математический тренажёр «Бабушкины примеры» Треугольники. Практика. Первый уровень
Треугольники. Практика. Первый уровень Путешествия на тропинках математики
Путешествия на тропинках математики Координаты вектора
Координаты вектора Кружок Занимательная математика
Кружок Занимательная математика Таблицы сложения и вычитания с числом 2
Таблицы сложения и вычитания с числом 2 Случайные процессы
Случайные процессы Степень числа. Квадрат и куб числа. Математика, 5 класс
Степень числа. Квадрат и куб числа. Математика, 5 класс Прямая в пространстве
Прямая в пространстве Проценты. 5 класс. Урок № 3
Проценты. 5 класс. Урок № 3