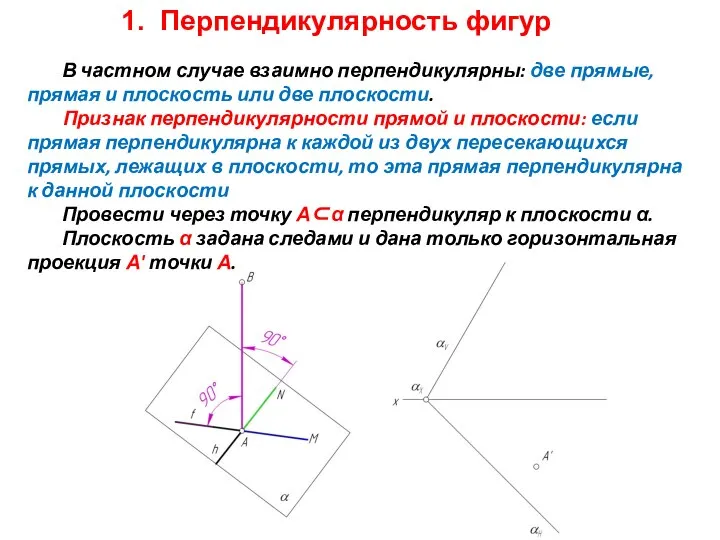
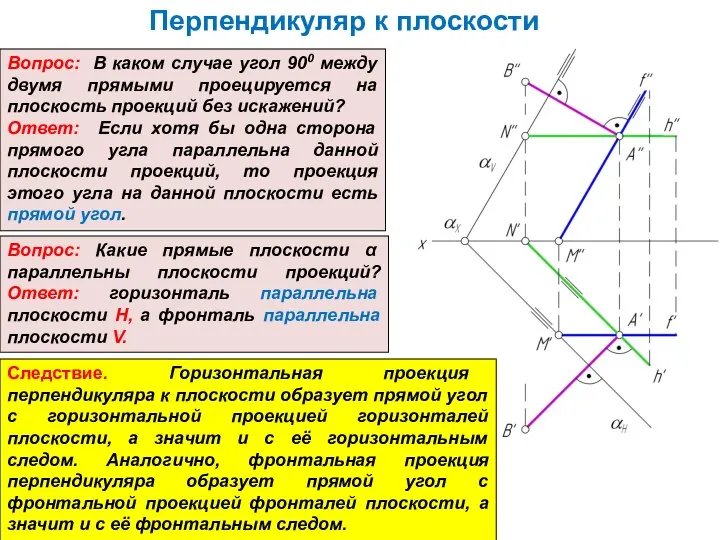
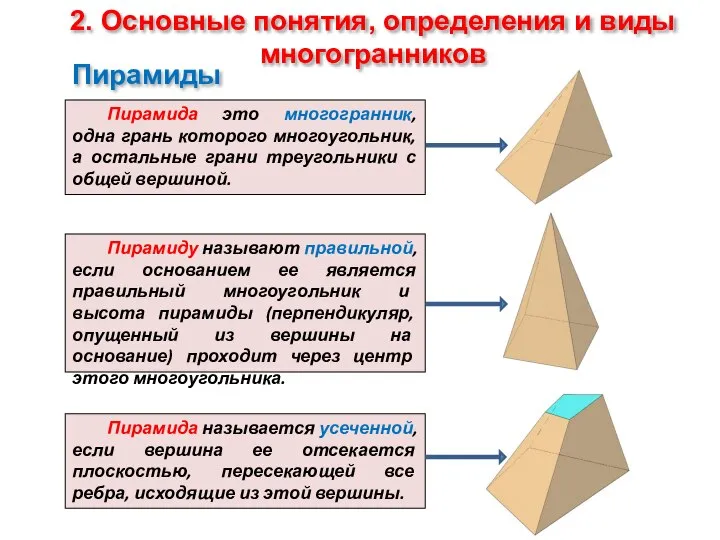
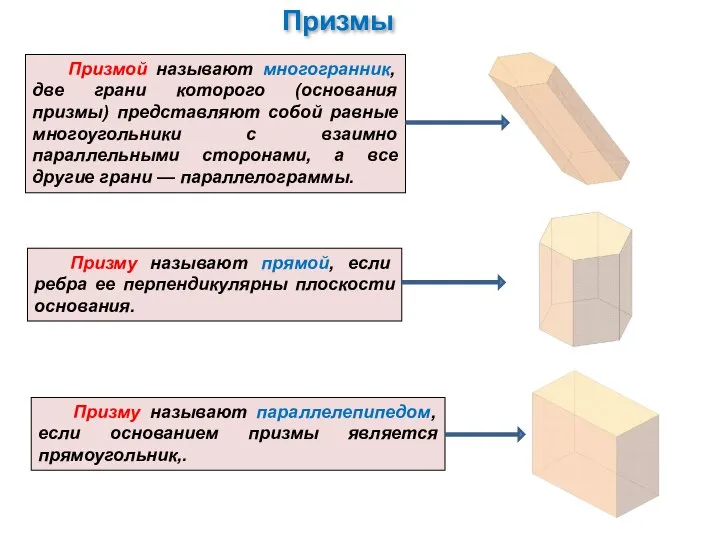
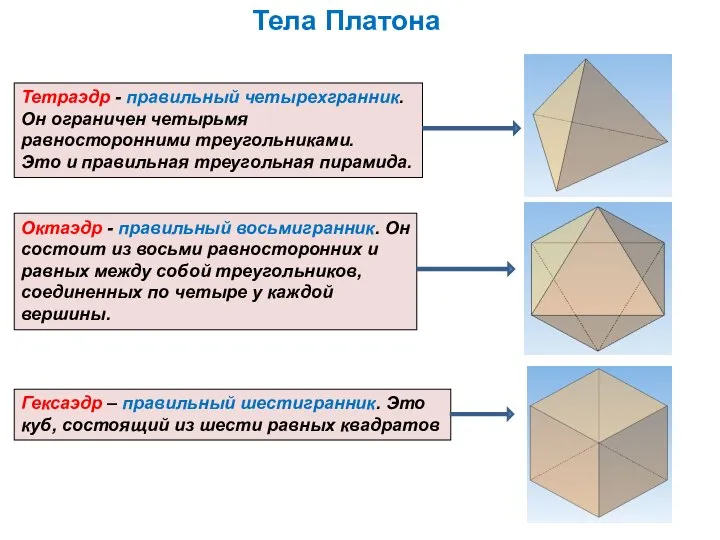
Перпендикуляр к плоскости
Вопрос: В каком случае угол 900 между двумя прямыми
проецируется на плоскость проекций без искажений?
Ответ: Если хотя бы одна сторона прямого угла параллельна данной плоскости проекций, то проекция этого угла на данной плоскости есть прямой угол.
Вопрос: Какие прямые плоскости α параллельны плоскости проекций? Ответ: горизонталь параллельна плоскости Н, а фронталь параллельна плоскости V.
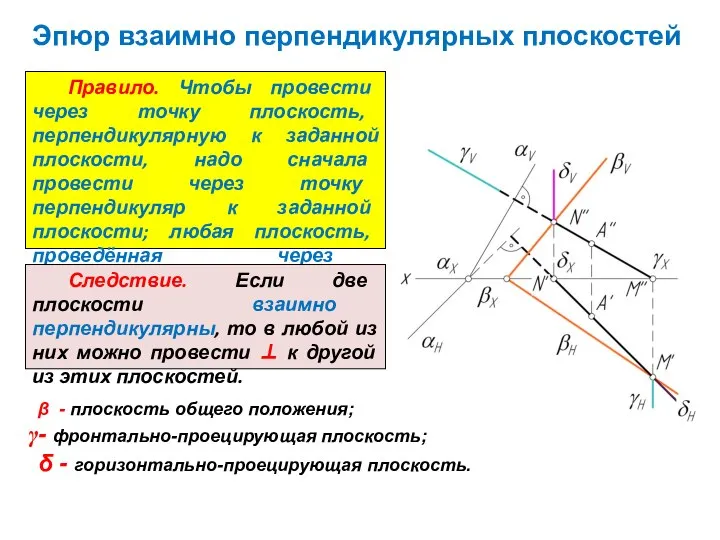
Следствие. Горизонтальная проекция перпендикуляра к плоскости образует прямой угол с горизонтальной проекцией горизонталей плоскости, а значит и с её горизонтальным следом. Аналогично, фронтальная проекция перпендикуляра образует прямой угол с фронтальной проекцией фронталей плоскости, а значит и с её фронтальным следом.
 Наибольший общий делитель
Наибольший общий делитель Аттестационная работа. Эссе о включении учащихся в проектную деятельность на уроках математики
Аттестационная работа. Эссе о включении учащихся в проектную деятельность на уроках математики Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Устный счет. Арифметический корень натуральной степени
Устный счет. Арифметический корень натуральной степени Теорема Пифагора (теорема нимфы, теорема невесты)
Теорема Пифагора (теорема нимфы, теорема невесты)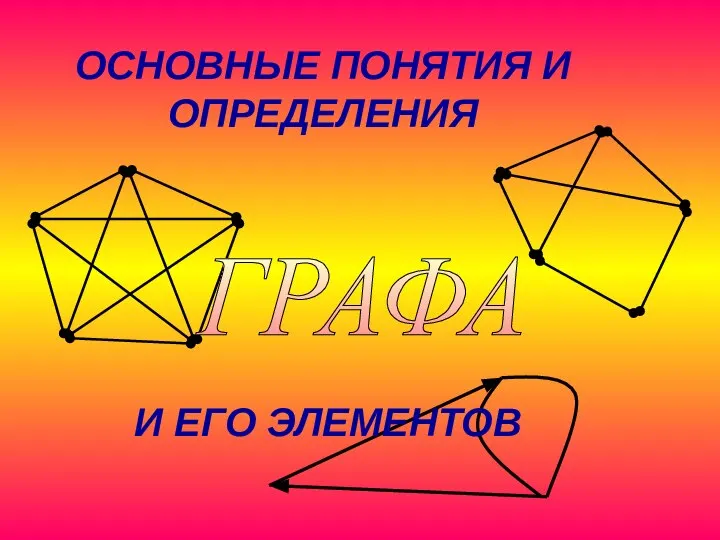 Основные понятия и определения графа и его элементов
Основные понятия и определения графа и его элементов Задачи на проценты 2
Задачи на проценты 2 Серединный перпендикуляр
Серединный перпендикуляр Аттестационная работа. Математическое общество учащихся Ориентир
Аттестационная работа. Математическое общество учащихся Ориентир Решение задач по теме «Векторы»
Решение задач по теме «Векторы» Булевы отношения
Булевы отношения Как путешествует точка? 6 класс
Как путешествует точка? 6 класс Аналитическая геометрия
Аналитическая геометрия Задача оптимизации
Задача оптимизации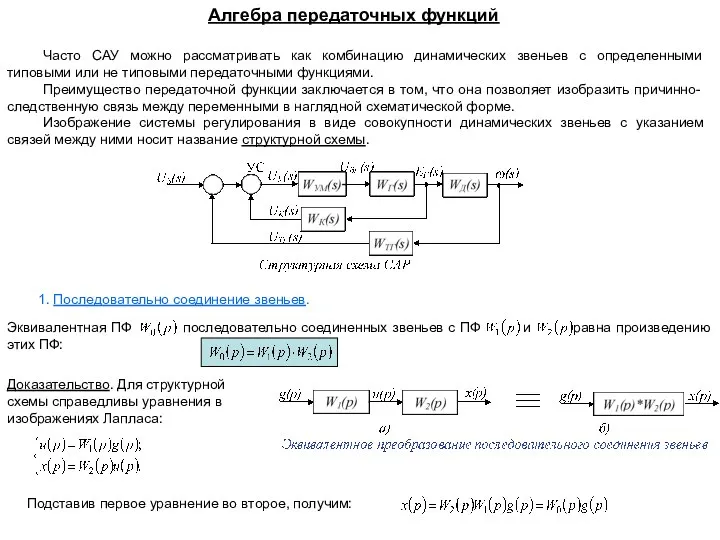 Алгебра передаточных функций
Алгебра передаточных функций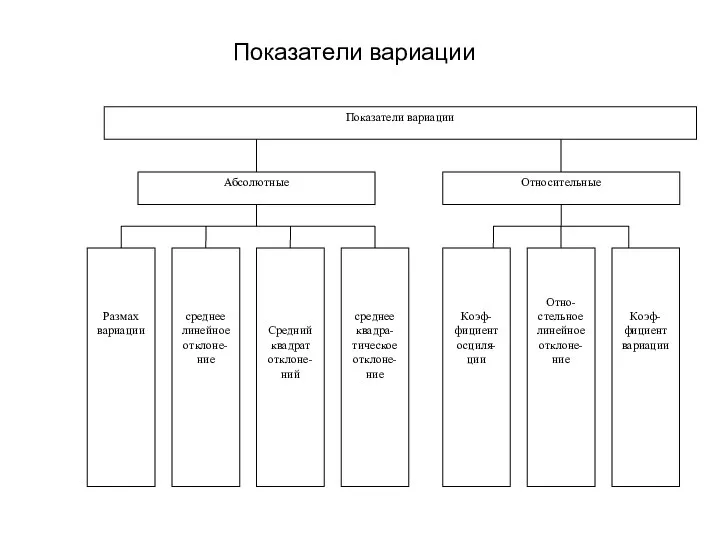 Показатели вариации
Показатели вариации Презентация на тему Сложение и вычитание в пределах 20
Презентация на тему Сложение и вычитание в пределах 20  Математика в жизни человека Киреева Ольга и Пономарёва Анастасия ученицы 6 класса МБОУ ООШ с.Никольское.
Математика в жизни человека Киреева Ольга и Пономарёва Анастасия ученицы 6 класса МБОУ ООШ с.Никольское. В царстве чисел-великанов. (6 класс)
В царстве чисел-великанов. (6 класс) Решение тригонометрических уравнений функционально-графическим методом
Решение тригонометрических уравнений функционально-графическим методом Графики, уравнения, неравенства
Графики, уравнения, неравенства Формула разности квадратов. 7 класс
Формула разности квадратов. 7 класс Шар. Задачи
Шар. Задачи Пропорции и отношения
Пропорции и отношения Рисуем по координатам
Рисуем по координатам Сумма углов треугольника
Сумма углов треугольника Система линейных уравнений с двумя переменными
Система линейных уравнений с двумя переменными 8 способов решения квадратного уравнения. 8 класс
8 способов решения квадратного уравнения. 8 класс