Содержание
- 2. Рассматриваемые показатели эффективности СМО с отказами A - абсолютную пропускную способность СМО, т.е. среднее число заявок,
- 3. Рассмотрим классическую задачу Эрланга Условие: Имеется n каналов, на которые поступает поток заявок с интенсивностью λ.
- 4. Нумерация по числу заявок Система S (СМО) имеет следующие состояния (нумеруем их по числу заявок, находящихся
- 5. Граф состояний СМО Граф состояний СМО соответствует процессу гибели и размножения и показан на рисунке: Поток
- 6. Схема гибели и размножения Для схемы гибели и размножения получим для предельной вероятности состояния формулу: где
- 7. Формулы Эрланга Последние формулы для предельных вероятностей получили названия формул Эрланга в честь основателя теории массового
- 8. Относительная пропускная способность Относительная пропускная способность – вероятность того, что заявка будет обслужена:
- 9. Среднее число занятых каналов
- 10. Пример решения задачи Эрланга Условие: Контроль представляет собой открытую многоканальную систему массового обслуживания с отказом в
- 11. Пример решения задачи Эрланга
- 12. Пример решения задачи Эрланга
- 13. Пример решения задачи Эрланга
- 14. Пример решения задачи Эрланга
- 16. Скачать презентацию













 Приёмы устных вычислений вида: 470+80, 560-90
Приёмы устных вычислений вида: 470+80, 560-90 Добери знак
Добери знак Противоположные числа Какие числа называют противоположными? Как на координатной прямой располагаются точки, соответствующие п
Противоположные числа Какие числа называют противоположными? Как на координатной прямой располагаются точки, соответствующие п Элементы теории вероятностей
Элементы теории вероятностей Длина окружности. Коллекция задач для 6 класса
Длина окружности. Коллекция задач для 6 класса Матриці та дії над ними. Поняття і види матриць
Матриці та дії над ними. Поняття і види матриць Первообразная и неопределённый интеграл
Первообразная и неопределённый интеграл Свойства двойного интеграла
Свойства двойного интеграла Дифференциал функции
Дифференциал функции Метрология. Основные понятия
Метрология. Основные понятия Правильные многоугольники
Правильные многоугольники Арифметическая и геометрическая прогрессии Учитель математики МБОУ «Адаевская ООШ» Актанышского муниципального района Респу
Арифметическая и геометрическая прогрессии Учитель математики МБОУ «Адаевская ООШ» Актанышского муниципального района Респу Презентация по математике "Теорема Пифагора" -
Презентация по математике "Теорема Пифагора" -  Многогранники. Все формулы. Геометрия (10-11 класс)
Многогранники. Все формулы. Геометрия (10-11 класс) Математическое моделирование. Значимость коэффициентов регрессии
Математическое моделирование. Значимость коэффициентов регрессии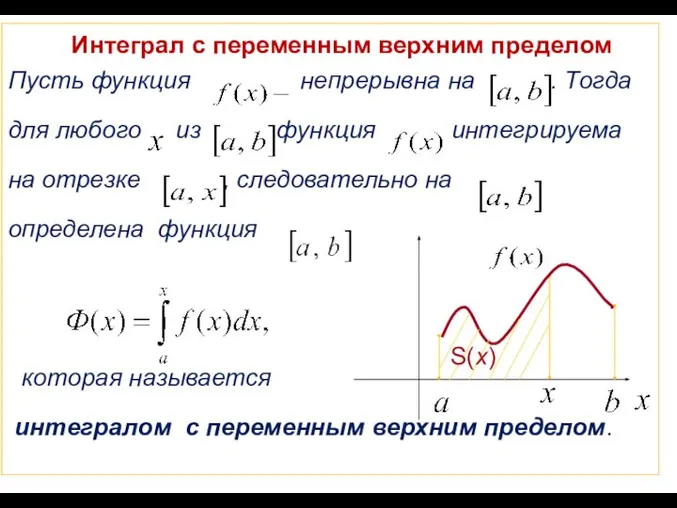 Интеграл с переменным верхним пределом
Интеграл с переменным верхним пределом Количественные характеристики случайной величины. Описательная статистика. (Лекция 4)
Количественные характеристики случайной величины. Описательная статистика. (Лекция 4) Математические забавы
Математические забавы Построение информационной модели метода изготовления изделия
Построение информационной модели метода изготовления изделия Применение подобия к доказательству теорем и решению задач. Урок 38
Применение подобия к доказательству теорем и решению задач. Урок 38 Площа бічної та повної поверхонь конуса
Площа бічної та повної поверхонь конуса Математика вокруг нас. Внеклассное мероприятие
Математика вокруг нас. Внеклассное мероприятие Презентация по математике "Упрощение выражений 6 класс" - скачать
Презентация по математике "Упрощение выражений 6 класс" - скачать  Практикум по решению задачи №20 (базовый уровень). ЕГЭ
Практикум по решению задачи №20 (базовый уровень). ЕГЭ Размещение из N элементов по k (k ≤ n)
Размещение из N элементов по k (k ≤ n) Число 14. Многоугольники
Число 14. Многоугольники Иррациональные неравенства. Виды и способы решения
Иррациональные неравенства. Виды и способы решения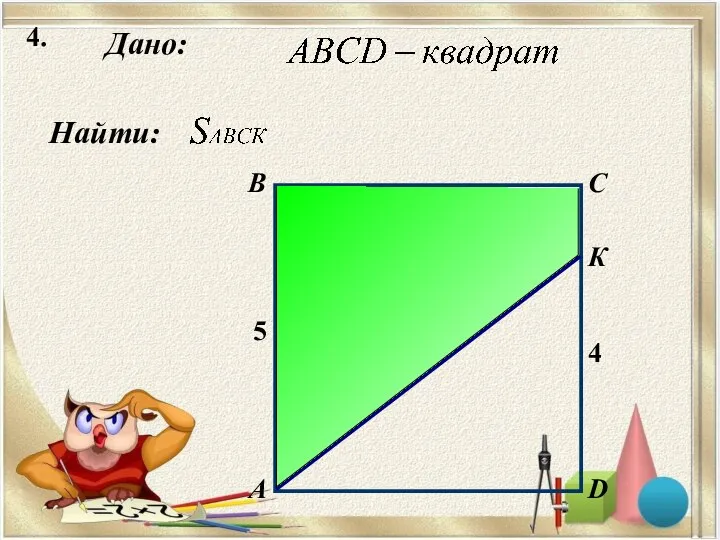 Решение задач на площадь треугольника
Решение задач на площадь треугольника