Слайд 3
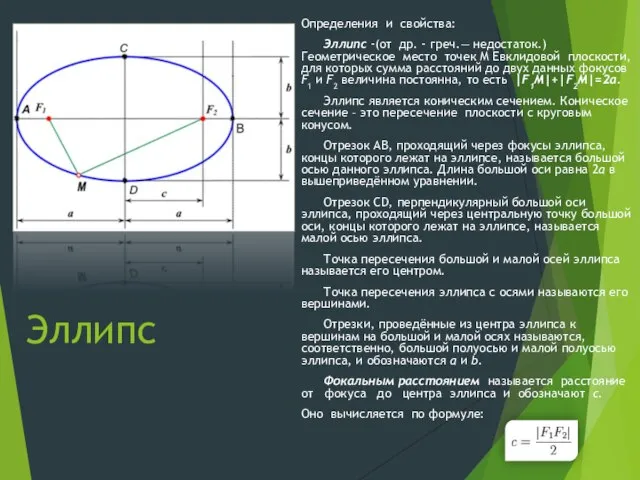
Эллипс
Определения и свойства:
Эллипс -(от др. - греч.— недостаток.) Геометрическое
место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных фокусов F1 и F2 величина постоянна, то есть |F1M|+|F2M|=2a.
Эллипс является коническим сечением. Коническое сечение – это пересечение плоскости с круговым конусом.
Отрезок AB, проходящий через фокусы эллипса, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
Точка пересечения большой и малой осей эллипса называется его центром.
Точка пересечения эллипса с осями называются его вершинами.
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
Фокальным расстоянием называется расстояние от фокуса до центра эллипса и обозначают c.
Оно вычисляется по формуле:


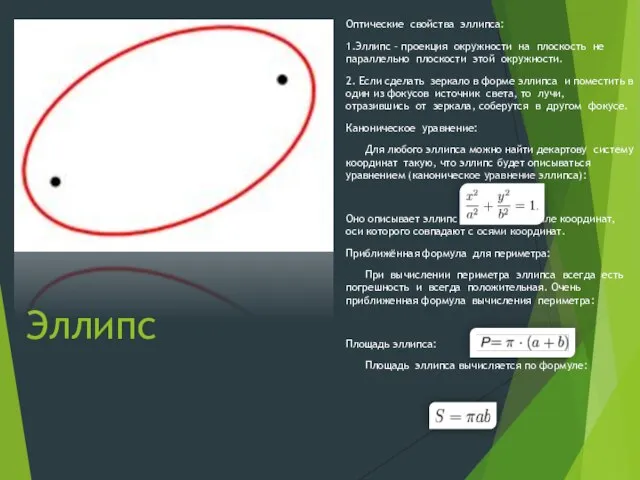





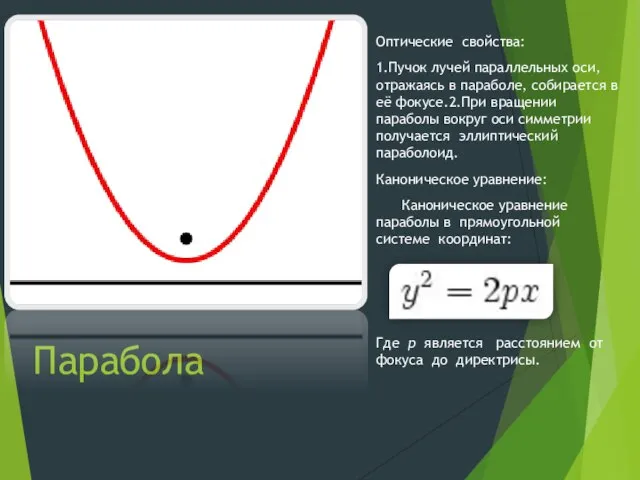
 Десятичные дроби. Путешествие на математическом поезде
Десятичные дроби. Путешествие на математическом поезде Числа 1-5. Закрепление изученного
Числа 1-5. Закрепление изученного Параллелепипед построение
Параллелепипед построение Презентация на тему Элементы статистики.
Презентация на тему Элементы статистики.  Source coordinate definition by. Non-destructive assay
Source coordinate definition by. Non-destructive assay Тренажёр. Счёт 1 - 20
Тренажёр. Счёт 1 - 20 Дифференциальные уравнения
Дифференциальные уравнения Перпендикулярные прямые
Перпендикулярные прямые Производная функции
Производная функции Математика в искусстве
Математика в искусстве Математический вечер "Ох, уж эта математика"
Математический вечер "Ох, уж эта математика" Числа в традиционном менталитете
Числа в традиционном менталитете Конусы в нашей жизни
Конусы в нашей жизни  Тетраэдр. Сечение тетраэдра
Тетраэдр. Сечение тетраэдра Платоновы тела и тайна мироздания
Платоновы тела и тайна мироздания Көп, аз, теңбе-тең
Көп, аз, теңбе-тең Устные упражнения. Выразите в процентах
Устные упражнения. Выразите в процентах Функция y=ах2+bx+c, ее свойства и график
Функция y=ах2+bx+c, ее свойства и график Математическая логика. Предмет математической логики
Математическая логика. Предмет математической логики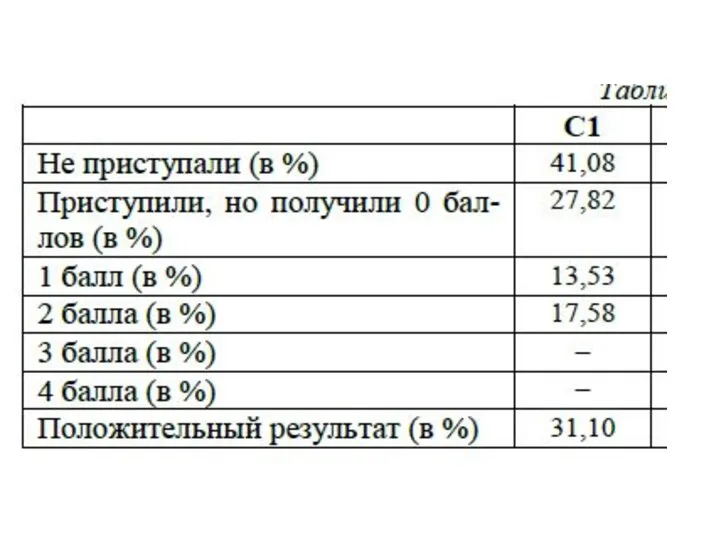 Некоторые особенности решения уравнений С1–С6 ЕГЭ
Некоторые особенности решения уравнений С1–С6 ЕГЭ Презентация по математике "Переместительное свойство сложения" - скачать бесплатно
Презентация по математике "Переместительное свойство сложения" - скачать бесплатно Первообразная. Неопределенный интеграл
Первообразная. Неопределенный интеграл Задачи на готовых чертежах. Квадрат
Задачи на готовых чертежах. Квадрат Презентация по математике "Равновеликие и равносоставленные плоские фигуры" - скачать
Презентация по математике "Равновеликие и равносоставленные плоские фигуры" - скачать  Способы решения систем уравнений (2)
Способы решения систем уравнений (2) Тренажер по арифметике для начальных классов. Задачи на сложение и вычитание
Тренажер по арифметике для начальных классов. Задачи на сложение и вычитание Десятичные дроби Понятие десятичной дроби. План: Немного истории Новая запись чисел Алгоритм десятичной записи Таблица разряд
Десятичные дроби Понятие десятичной дроби. План: Немного истории Новая запись чисел Алгоритм десятичной записи Таблица разряд Число 8. Цифра 8
Число 8. Цифра 8