Содержание
- 2. Следует повторить Понятие и виды экспертных оценок Шкалы и допустимые преобразования Проверка статистических гипотез Критическая точка
- 3. Входной контроль Укажите допустимые преобразования для заданных типов шкал
- 4. Самопроверка
- 5. План лекции Математические методы обработки и анализа экспертных оценок Стандартизация рангов Метод согласования кластеризованных ранжировок Оценка
- 6. Методы обработки экспертных оценок Обработка результатов коллективной экспертизы направлена на согласование позиций специалистов с целью выработки
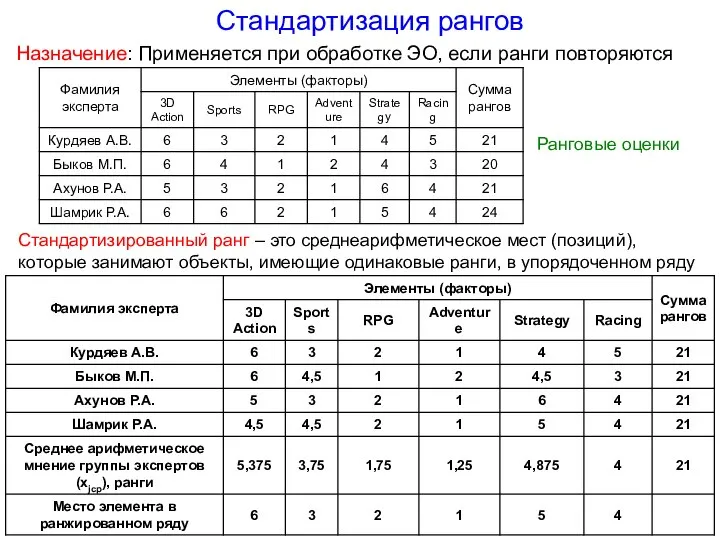
- 7. Стандартизация рангов Назначение: Применяется при обработке ЭО, если ранги повторяются Ранговые оценки Стандартизированный ранг – это
- 8. Метод согласования кластеризованных ранжировок
- 9. Кластеризованная ранжировка Ранжирование - расположение исследуемых объектов в порядке возрастания (или убывания) какого-либо присущего им свойства
- 10. Кластеризованная ранжировка в виде матрицы бинарного отношения Кластеризованную ранжировку, (как и любое бинарное отношение), можно задать
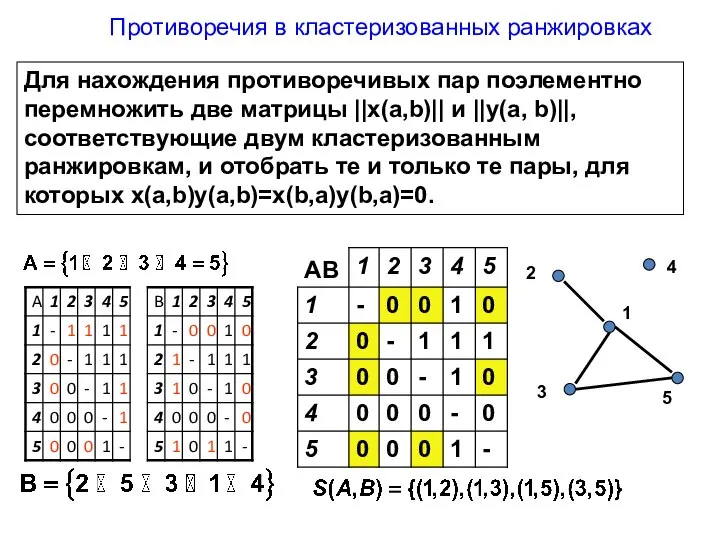
- 11. Пусть А и В – две кластеризованные ранжировки. Пару объектов (a,b) назовем «противоречивой» относительно кластеризованных ранжировок
- 12. Пусть А и В – две кластеризованные ранжировки. Пару объектов (a,b) назовем «противоречивой» относительно кластеризованных ранжировок
- 13. Пусть А и В – две кластеризованные ранжировки. Пару объектов (a,b) назовем «противоречивой» относительно кластеризованных ранжировок
- 14. Пример. Ядро противоречий ранжировок В и С S(B,C) = (1, 3), (2, 3), (2, 4), (5,
- 15. Противоречия в кластеризованных ранжировках Для нахождения противоречивых пар поэлементно перемножить две матрицы ||x(a,b)|| и ||y(a, b)||,
- 16. Выделяются противоречивые пары объектов во всех парах кластеризованных ранжировок. Формируются кластеры итоговой кластеризованной ранжировки (т.е. классы
- 17. Пример
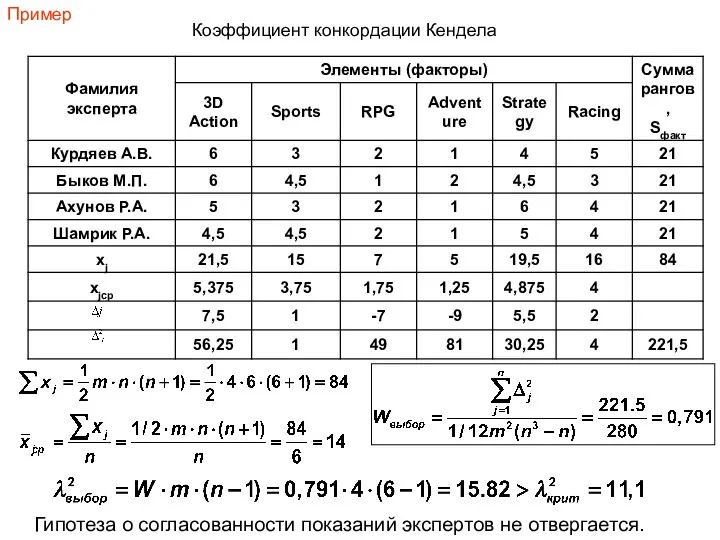
- 18. Если то гипотеза о согласованности показаний экспертов не отвергается; иначе - отвергается 3 Вычисляем фактические отклонения
- 19. Коэффициент конкордации Кендела jср Гипотеза о согласованности показаний экспертов не отвергается. Пример
- 20. Поиск результирующего ранжирования Если оценки экспертов согласованы, то для поиска результирующего ранжирования можно использовать метод средних
- 21. 1. Взять ответы экспертов, соответствующие одному из объектов, 2. Расположить их в порядке неубывания (если нет
- 22. Расстояние Кемени Определение. Расстоянием Кемени между ранжировками А и В, описываемыми матрицами || a(i,j) || и
- 23. Алгоритм Кемени-Снелла Пусть А1 , А2 , А3 ,…, Ар - ответы р экспертов, представленные в
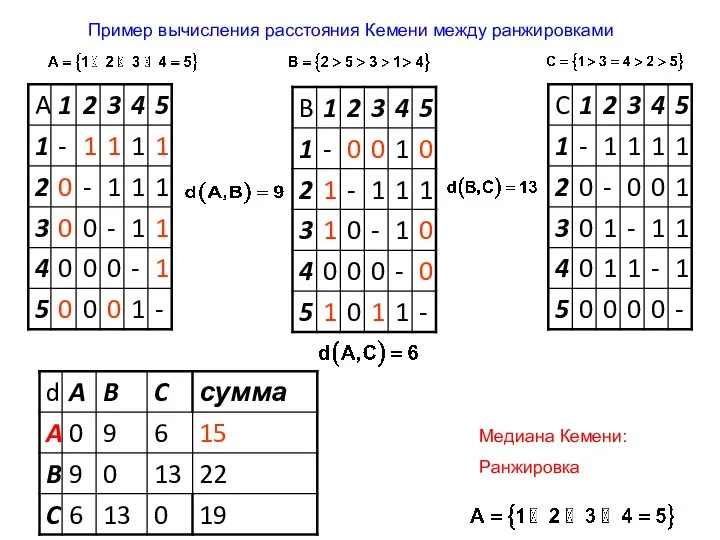
- 24. Пример вычисления расстояния Кемени между ранжировками Медиана Кемени: Ранжировка
- 25. Автоматизация ЭО * Вычисление результирующей экспертной оценки, а также классификация мнений экспертов реализованы в пакете STATISTICA
- 27. Скачать презентацию



















 Отчет по производственной и преддипломной практики
Отчет по производственной и преддипломной практики Аттестационная работа. Рабочая программа курса внеурочной деятельности Я - исследователь. (7 класс)
Аттестационная работа. Рабочая программа курса внеурочной деятельности Я - исследователь. (7 класс) Входное тестирование. ЕГЭ по обществознанию
Входное тестирование. ЕГЭ по обществознанию Пилотные группы РОСТЕХ (год поступления - 2021 г.)
Пилотные группы РОСТЕХ (год поступления - 2021 г.) Мониторинг, как важнейшее звено управления инновационными процессами в системе образования
Мониторинг, как важнейшее звено управления инновационными процессами в системе образования Формирование специалистами ДОУ цифровой образовательной среды в условиях реализации ФГОС ДО
Формирование специалистами ДОУ цифровой образовательной среды в условиях реализации ФГОС ДО Central European University
Central European University Санкт-Петербургский Государственный Университет Промышленных технологий и дизайна
Санкт-Петербургский Государственный Университет Промышленных технологий и дизайна Организация проведения государственной итоговой аттестации в ОЧУВО Международный инновационный университет в 2018 году
Организация проведения государственной итоговой аттестации в ОЧУВО Международный инновационный университет в 2018 году Аттестационная работа. Система работы с одарёнными детьми интеллектуальной направленности
Аттестационная работа. Система работы с одарёнными детьми интеллектуальной направленности Об образовании в Российской Федерации по вопросам воспитания обучающихся
Об образовании в Российской Федерации по вопросам воспитания обучающихся Дополнительные общеобразовательные общеразвивающие программы
Дополнительные общеобразовательные общеразвивающие программы Высшее образование в России
Высшее образование в России Характеристика образовательного центра в Великобритании
Характеристика образовательного центра в Великобритании Рыбинский промышленно-экономический колледж
Рыбинский промышленно-экономический колледж BEO (British English Olympics)
BEO (British English Olympics) Ими гордится факультет математики, механики и компьютерных наук. 2015 – 2016 учебный год
Ими гордится факультет математики, механики и компьютерных наук. 2015 – 2016 учебный год Приемная комиссия УГУ
Приемная комиссия УГУ Why i want to be a prosecutor
Why i want to be a prosecutor Інновації у роботі з першокласниками
Інновації у роботі з першокласниками Развитие саморегуляции младших школьников в процессе овладения регулятивными универсальными учебными действиями
Развитие саморегуляции младших школьников в процессе овладения регулятивными универсальными учебными действиями Любецкий А.Г. 25.08.2020
Любецкий А.Г. 25.08.2020 Аттестационная работа. Учебно-исследовательская деятельность студентов по дисциплине Основы маркетинга
Аттестационная работа. Учебно-исследовательская деятельность студентов по дисциплине Основы маркетинга Аттестационная работа. Планирование работы начальной школы, параллель 4-ых классов, в области проектной деятельности
Аттестационная работа. Планирование работы начальной школы, параллель 4-ых классов, в области проектной деятельности Аттестационная работа. Образовательная программа кружка Юные друзья полиции
Аттестационная работа. Образовательная программа кружка Юные друзья полиции Азаматтардың бiлiм алу құқы ҚР Конситутциясында кепiлденген және 1999жылы маусым айының 7 жұлдызында қабылданған “Бiлiм беру
Азаматтардың бiлiм алу құқы ҚР Конситутциясында кепiлденген және 1999жылы маусым айының 7 жұлдызында қабылданған “Бiлiм беру Влияние занятий музыкой на успеваемость в школе
Влияние занятий музыкой на успеваемость в школе Формы организации учебного процесса. Лабораторные (практические) занятия
Формы организации учебного процесса. Лабораторные (практические) занятия