Содержание
- 2. Простейший тип дискретного источника – это такой, который выдаёт последовательность букв (символов), выбираемых из определенного алфавита.
- 3. Чтобы конструировать математическую модель для дискретного источника предположим, что каждый символ алфавита {x1, x2, …, xL}
- 4. Рассмотрим две математические модели для дискретных источников. Предположим, что символы выходной последовательности источника статистически независимы, т.е.
- 5. Если отдельные выходные символы дискретного источника статистически взаимозависимы, как, например, в английском тексте, мы можем сконструировать
- 6. Аналоговый источник выдает сигнал x(t), который является реализацией случайного процесса X(t). Предположим, что X(t) - стационарный
- 7. Где X{(n/2W)} - отсчёты процесса X(t) взятые со скоростью Найквиста fs=2W, 1/c. Используя теорему отсчётов, мы
- 8. Заметим, что выходные отсчёты стационарного источника обычно непрерывны, и, следовательно, их нельзя представить в цифровой форме
- 9. «ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ»
- 10. Чтобы разработать подходящую меру для информации, рассмотрим две дискретные случайные величины X и Y с возможными
- 11. Заметим, что если X и Y статистически не зависят друг от друга, выбор Y=yj не даёт
- 12. Подходящая мера информации, которая удовлетворяет указанным условиям, - это логарифм отношения условной вероятности: P(X=xi | Y=yj)=P(xi
- 13. Это значит, что количество информации, полученное при появлении события Y=yj относительно события X=xi определяется как: названа
- 14. Единица измерения I(xi;yj) определяется основанием логарифма, в качестве которой обычно выбирается или 2, или е. Когда
- 15. Когда случайные величины X и Y статистически независимы, то P(xi|yj)=P(xi), следовательно, I(xi; yj)=0. С другой стороны,
- 16. Но (2) как раз определяет информацию X=xi Исходя из этих соображений, её называют собственной информацией события
- 17. Пример 1 Предположим, что имеется дискретный источник, который выдаёт двоичную цифру 0 или 1 с равной
- 18. Теперь предположим, что последовательные цифры на выходе источника статистически независимы, т.е. источник не имеет памяти. Рассмотрим
- 19. Она выдаётся на временном интервале Kτx. Таким образом, логарифмическая мера количества информации обладает желаемыми свойствами аддитивности,
- 20. вернёмся к определению взаимной информации, определяемой (1), и умножим числитель и знаменатель отношения вероятностей на p(yj)
- 21. Таким образом, информация, содержащаяся в выборе события Y=yj относительно события X=xi идентична информации, содержащейся в выборе
- 22. Пример 2 Предположим, что X и Y -двоичные {0,1} случайные величины, представляющие вход и выход канала
- 23. Определим, сколько информации об X=0 и X=1 содержится в событии Y=0 . Из заданных вероятностей получим:
- 24. Рассмотрим несколько частных случаев. В первом, когда, p0=p1=0 канал называют каналом без шумов и I(0;0)=log22=1бит. Следовательно,
- 25. Помимо определения взаимной информации и собственной информации полезно определить условную собственную информацию как: (5) Тогда, комбинируя
- 26. Мы интерпретируем I(xi|yj) как собственную информацию о событии X=xi после наблюдения события Y=yj . Из условия
- 27. «Средняя взаимная информация и энтропия»
- 28. Зная взаимную информацию, связанную с парой событий (xi;yj), которые являются возможной реализацией двух случайных величин X
- 29. Таким образом получим: как среднюю взаимную информацию между X и Y (1)
- 30. Видно, что I(X;Y)=0, когда X и Y статистически независимы и P(xi;yj)=P(xi)P(yj) Важным свойством средней взаимной информации
- 31. Аналогично определим среднюю собственную информацию, обозначенную H(X) (2) Если X представляет собой алфавит возможных символов источника,
- 32. В общем случае H(X) ≤ logn при любых заданных вероятностях символов источника. Другими словами, энтропия источника
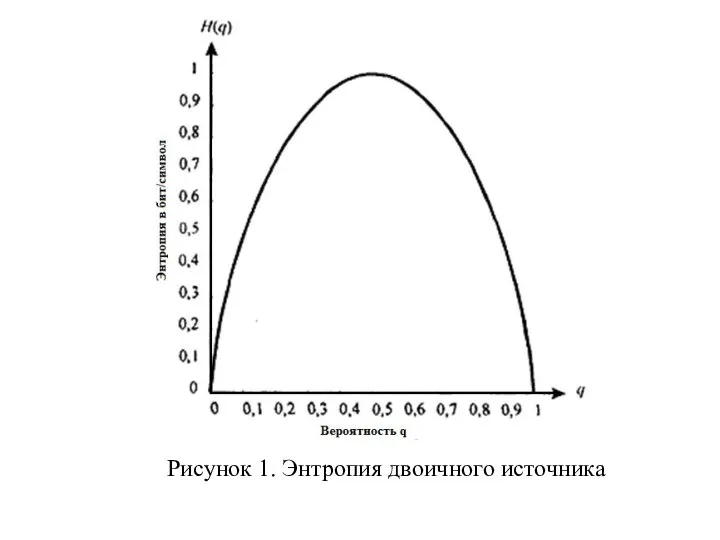
- 33. Пример 1 Рассмотрим двоичный источник, который выдаёт последовательности независимых символов, причём выходной кодовый символ «0» с
- 34. Рисунок 1. Энтропия двоичного источника
- 35. Среднее значение условной собственной информации называется условной энтропией и определяется как: Мы интерпретируем H(X|Y) как неопределённость
- 36. Из условия I(X,Y) ≥0 следует, что H(X)≥H(X|Y) и H(Y)≥H(Y|X), причём равенство имеет место тогда, и только
- 37. т.е. имевшейся до наблюдения, тогда I(X;Y) определяет взаимную информацию (уменьшение среднего значения неопределённости, имеющейся относительно X
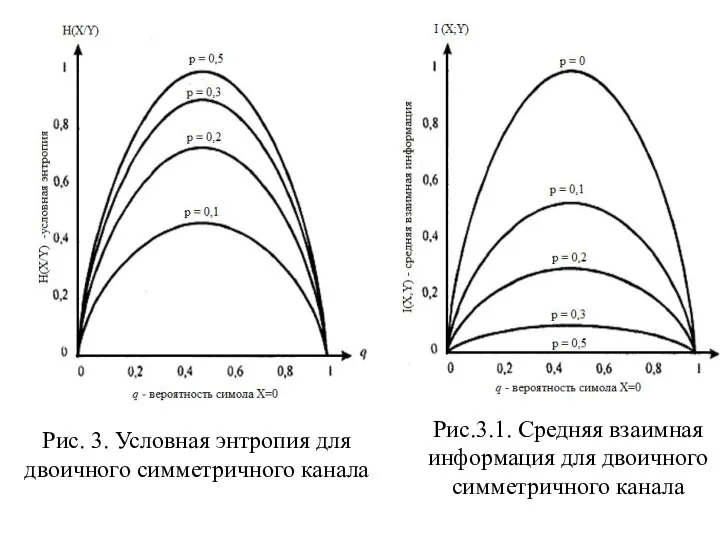
- 38. Пример 2 Определим H(X|Y) и I(X,Y) для канала с двоичным входом и выходом, рассмотренного выше в
- 39. Рис.3.1. Средняя взаимная информация для двоичного симметричного канала Рис. 3. Условная энтропия для двоичного симметричного канала
- 40. Когда условную энтропию H(X|Y) рассматривают применительно к каналу с входом и выходом Y, то называют ненадёжностью
- 41. Результаты, приведённые выше, легко обобщаются на случай произвольного числа случайных величин. В частности, предположим, что мы
- 42. Тогда энтропия определяется как: Поскольку совместную вероятность P(X1X2…,Xk) можно выразить в виде: P(x1x2…xk)≡P(x1)P(x2|x1)P(x3|x1x2)…P(xk|x1x2…xk-1) то следует (7)
- 43. С учётом результата H(X)≥H(X|Y) где X=Xm и Y=X1X2…Xm-1 из (7) следует причём равенство имеет место тогда,
- 44. «Кодирование для дискретных источников без памяти»
- 45. Предположим, что ДИБП выдает буквы или символы каждые τx секунд. Каждый символ выбирается из конечного алфавита
- 46. Кодовые слова фиксированной длины Сначала рассмотрим схему блокового кодирования, которая сопоставляет уникальный ряд из R двоичных
- 47. когда L равно целой степени основания 2, и R=[log2 L]+1 когда не равно целой степени основания
- 48. R будем называть скоростью кодирования. Она определяет число символов кодера на один символ источника. Поскольку, H(X)
- 49. Если log L>>1, эффективность такой схемы кодирования высока. С другой стороны, если L мало, эффективность кода
- 50. Теперь среднее число символов кода на символ источника R=N/J , и, таким образом, неэффективность кодирования сокращается
- 51. Методы кодирования, не приводят к искажениям, так как кодирование символов источника или блоков таких символов в
- 52. Предположим, что мы пытаемся уменьшить скорость кодирования R путем смягчения условия однозначности процесса кодирования. Предположим, что
- 53. Теорема кодирования источника I Пусть X - это ансамбль символов ДИБП с конечной энтропией H(X). Блоки
- 54. Исходя из этой теоремы мы видим, что среднее число бит на символ источника требуемое для кодирования
- 55. Кодовые слова переменной длины
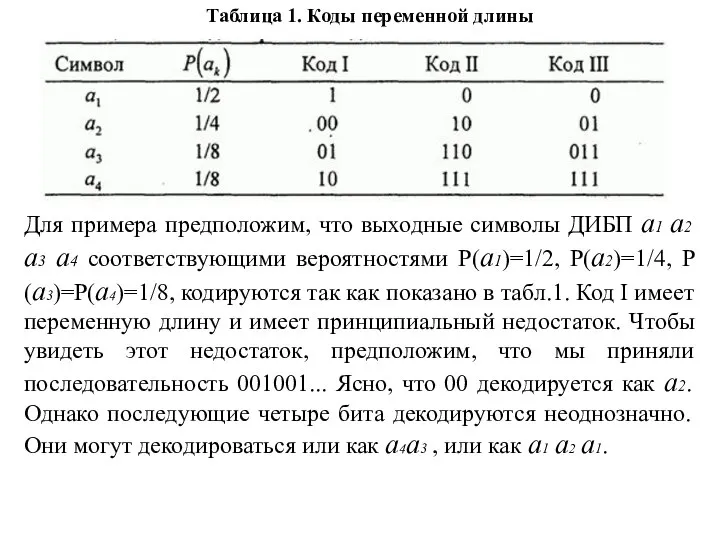
- 56. Если символы источника неравновероятны, более эффективный метод кодирования сводится к использованию кодовых слов переменной длины. Примером
- 57. Таблица 1. Коды переменной длины Для примера предположим, что выходные символы ДИБП а1 а2 а3 а4
- 58. Код II в табл. 1 обеспечивает однозначное и немедленное декодирование. Удобно представлять кодовые слова этого кода
- 59. Заметим, что ни одно кодовое слово этого кода не является префиксом (началом) другого кодового слова. В
- 60. Другими словами, нет кодовых слов длины l l. Это свойство делает кодовые слова немедленно декодируемыми. Код
- 61. Наша главная цель – создать систематическую процедуру для конструирования однозначных декодирующих кодов переменной длины, эффективных в
- 62. Неравенство Крафта Необходимым и достаточным условием существования двоичного кода с кодовыми символами длины n1 ≤ n2
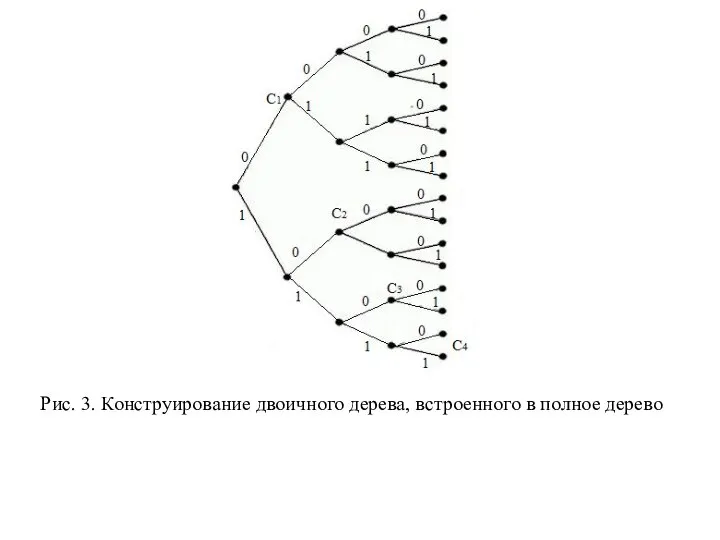
- 63. Выберем некоторый узел порядка в качестве первого кодового слова C1. Этот выбор устраняет конечных узлов. От
- 64. Таким образом, создали кодовое дерево, которое встроено в полное дерево из узлов, как иллюстрируется на рис.
- 65. Рис. 3. Конструирование двоичного дерева, встроенного в полное дерево
- 66. Чтобы доказать, что (2) является необходимым условием, мы заметим, что в дереве порядка n = nL
- 67. Теорема кодирования источника II. Пусть X- ансамбль символов двоичного источника без памяти с конечной энтропией H(X)
- 68. Используя неравенство ln x ≤ x-1 , из (5) находим: Верхняя граница в (4) может быть
- 69. Если умножить обе части неравенства (6) на pk и просуммировать по 1 ≤ k ≤ L.
- 70. Алгоритм кодирования Хаффмена
- 71. Хаффмен (1952) разработал алгоритм кодирования переменной длины, основанный на знании априорных вероятностей символов P(xi), i=1,2,…L .
- 72. Пример 1. Рассмотрим ДИБГТ с семью возможными символами, имеющими вероятности выбора, иллюстрируемое ниже. Среднее число двоичных
- 73. Заметим, что полученный код не единственно возможный. Например, на предпоследнем шаге процедуры кодирования мы имеем равный
- 74. Рис. 2. Альтернативный код для ДИБП в примере 1
- 75. Пример 2. В качестве второго примера определим код Хаффмена для выхода ДИБП, иллюстрируемый на рис. 3.
- 76. Алгоритм кодирования переменной длины (Хаффмена), генерирует префиксный код, имеющий среднюю длину. Однако вместо посимвольного кодирования более
- 77. так как энтропия J -символьного блока от ДИБП равна JH(X), и RJ - среднее число бит
- 78. Рис. 3.Код Хаффмена для примера 2
- 79. Пример 3 Выход ДИБП состоит из символов x1, x2 и x3 с вероятностями 0,45, 0,35 и
- 80. Таблица 1. Код Хаффмена
- 81. Таблица 2. Код Хаффмена для кодирования пар символов
- 82. Дискретные стационарные источники
- 83. Рассмотрим дискретные источники, для которых последовательность символов выхода является статистически зависимой. Мы ограничим наше исследование источниками,
- 84. Оценим энтропию некоторой последовательности символов от стационарного источника. Энтропия блока случайных переменных X1 ,X2 … Xk
- 85. Мы определяем количество информации стационарного источника как энтропию на символ в (2) в пределе при ,
- 86. Этот результат также установлен ниже. Наше изложение использует подход Галлагера (1968). Во-первых, мы покажем, что: H(Xk|X1X2…Xk-1)≤
- 87. Во-вторых, мы имеем результат: Hk (X) ≥ H(Xk|X1X2...Xk-1) B-третьих, по определению Hk(X): что приводит к: Hk
- 88. Поскольку Hk (X) и условная энтропия H(Xk|X1X2…Xk-1) не отрицательны и не возрастающие (с ростом k), оба
- 89. Для фиксированного k в пределе для (10) при j→∞ получаем: H∞ (X) ≤ H(Xk|X1X2...Xk-1) Но (11)
- 90. Предположим, что мы имеем дискретный стационарный источник, который даёт J символов с энтропией на символ HJ(X).
- 91. Деля обе части (13) на J, мы получаем границы для среднего числа R=RJ /J бит на
- 92. Алгоритм Лемпела-Зива
- 93. Алгоритм кодирования Хаффмена приводит к оптимальному кодированию источника в том смысле, что кодовые слова удовлетворяют префиксному
- 94. В отличие от алгоритма кодирования Хаффмена алгоритм кодирования Лемпела-Зива разработан так, чтобы быть независимым от статистики
- 95. В алгоритме Лемпела-Зива последовательность с выхода дискретного источника делится на блоки переменной длины, которые называются фразами.
- 96. Рассмотрим бинарную последовательность : 10101101001001110101000011001110101100011011. Деление последовательности, как описано выше, производит следующие фразы: 1,0,10, 11,01,00. 100,
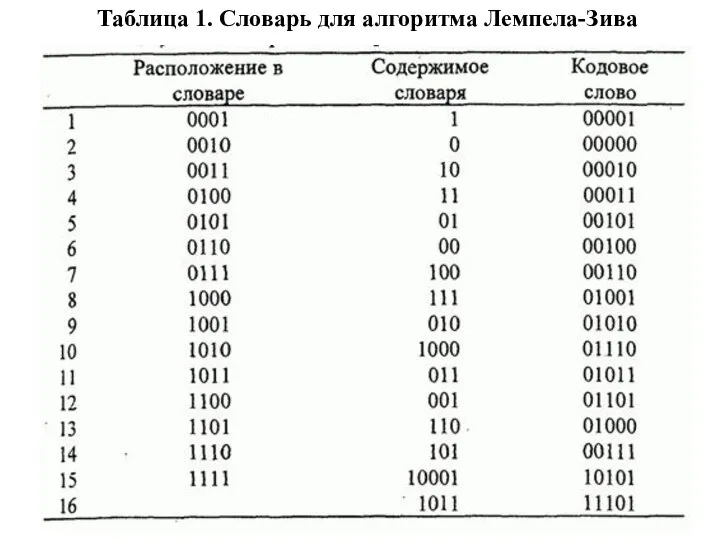
- 97. Таблица 1. Словарь для алгоритма Лемпела-Зива
- 98. Ячейки словаря пронумерованы последовательно, начиная с 1 и далее, в данном случае до 16, что является
- 99. Декодер источника создает идентичную таблицу на приемном конце системы связи и соответственно декодирует полученную последовательность. Можно
- 100. Алгоритм Лемпела-Зива широко используется при сжатии компьютерных файлов. «Сжимающие» и «разжимающие» программы (утилиты) в операционной системе
- 101. «Кодирование для аналоговых источников - оптимальное квантование»
- 102. Аналоговый источник выдаёт непрерывный сигнал x(t), который является выборочной функцией случайного процесса X(t). Если X(t) является
- 103. Применяя теорему отсчётов, выход аналогового источника преобразуется в эквивалентную дискретную во времени последовательность отсчётов. Затем отсчёты
- 104. Следовательно, если мы имеем L уровней, нам необходимы R=log2L бит/отсчёт (если L есть степень числа 2)
- 105. Квантование амплитуд дискретизированного во времени сигнала обеспечивает сжатие данных, но это также приводит к некоторому искажению
- 106. Функция скорость-искажение R(D) Под термином «искажение» мы понимаем некоторую меру разности между фактическими выборками источника {xk}
- 107. Используемое для определения ошибки квантования при ИКМ: (2) Где p- принимает значения из ряда положительных целых
- 108. На выходе источника имеет место случайный процесс, и, следовательно, n отсчётов Xn в являются случайными величинами.
- 109. где I(X,X)- средняя взаимная информация между X и X.Вообще, скорость R(D) уменьшается при увеличении D или,
- 110. «Функция скорость-искажение для гауссовского источника без памяти»
- 111. Теорема: Функция скорость-искажение для гауссовского источника без памяти (Шеннон, 1959). Минимальная скорость кодирования, необходимая для представления
- 112. Заметим, что (1) подразумевает, что, если искажение, D ≥ σx² никакой информации передавать не нужно. Конкретно
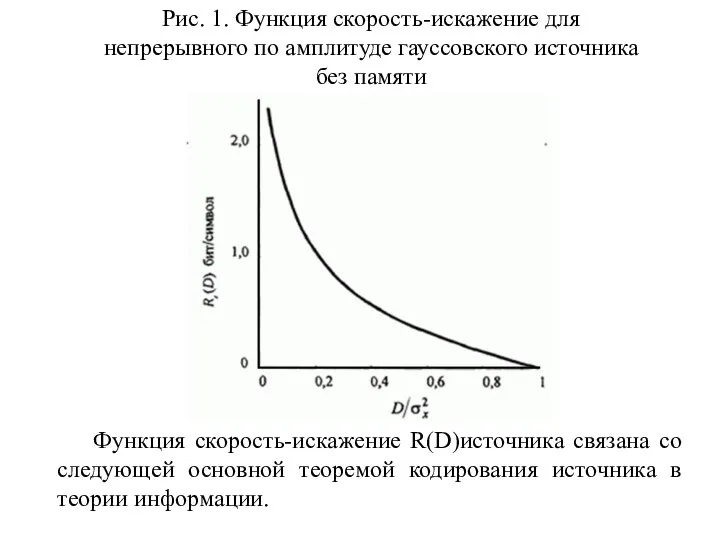
- 113. Рис. 1. Функция скорость-искажение для непрерывного по амплитуде гауссовского источника без памяти Функция скорость-искажение R(D)источника связана
- 114. Теорема: Кодирование источника с заданной мерой искажения (Шеннон, 1959). Существует схема кодирования, которая отображает выход источника
- 115. Вернёмся к результату в (1) для функции скорость-искажение гауссовского источника без памяти. Если мы поменяем функциональную
- 116. Верхняя граница для функции скорость-искажение
- 117. Теорема: Верхняя граница для R(D) Функция скорость-искажение непрерывного по амплитуде источника без памяти с нулевым средним
- 118. Доказательство этой теоремы дано Бергером (1971). Подразумевается, что гауссовский источник требует максимальную скорость кодирования среди всех
- 119. Существует также нижняя граница функции скорость-искажение. Её называют нижней границей Шеннона для среднеквадратической ошибки искажения, и
- 120. Следовательно, функция скорость-искажение для произвольного источника без памяти с непрерывной амплитудой ограничена сверху и снизу: R*(D)
- 121. так что нижняя граница R*(D) в (3) уменьшается до Rg(D).Теперь, если выразить D*(R) в децибелах и
- 122. В таблице 1 даны четыре типа ФПВ, которые являются моделями распределения, обычно используемыми для источника сигнала.
- 123. Таблица 1. Дифференциальная энтропия и сравнение скорости и искажений четырёх распространённых ФПВ для моделей сигнала
- 124. Следовательно, эквивалентный дискретный во времени гауссовский источник является источником без памяти. Поэтому функция скорость-искажение для белого
- 125. Скалярное квантование
- 126. При кодировании источника квантователь может быть оптимизирован, если известна ФПВ уровней сигнала на входе квантователя. Например,
- 127. В общем, оптимальный квантователь минимизирует D путём оптимального выбора выходных уровней и входного диапазона для каждого
- 128. У равномерного квантователя выходные уровни определяются как для амплитуды входного сигнала в диапазоне , где ∆-
- 129. В этом случае минимизация D выполняется с учётом параметра размера шага ∆. Путём дифференцирования D по
- 130. Для среднеквадратичного критерия ошибки, кода f(x)=x², Макс(1960) рассчитал оптимальный размер шага ∆опт и минимальное значение среднеквадратической
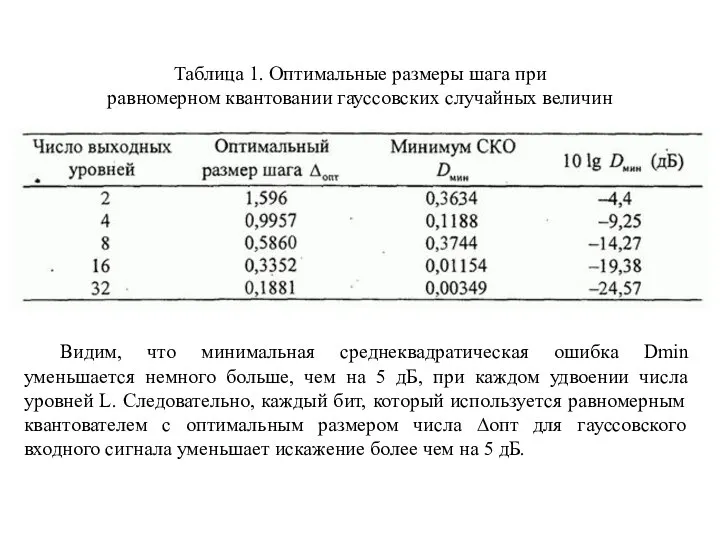
- 131. Таблица 1. Оптимальные размеры шага при равномерном квантовании гауссовских случайных величин Видим, что минимальная среднеквадратическая ошибка
- 132. Результирующее искажение: (4) снова минимизируется путём оптимального выбора Необходимые условия для минимальных искажений можно получить дифференцированием
- 133. Соответствующие уравнения, определяющие Таким образом, является центроидом области p(x) между xk-1 и xk. Эти уравнения могут
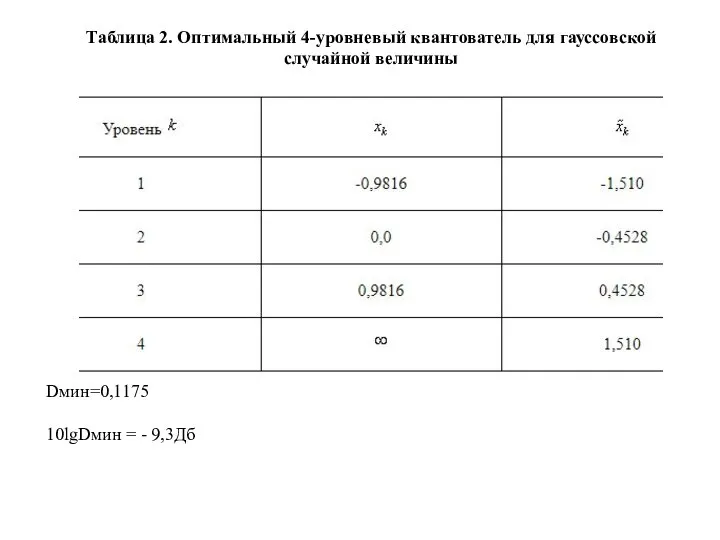
- 134. Таблица 2. Оптимальный 4-уровневый квантователь для гауссовской случайной величины Dмин=0,1175 10lgDмин = - 9,3Дб
- 135. Таблица 3. Оптимальный 8-уровневый квантизатор для гауссовской случайной величины (Макс, 1960) Dмин=0,03454 10lgDмин = - 14,62Дб
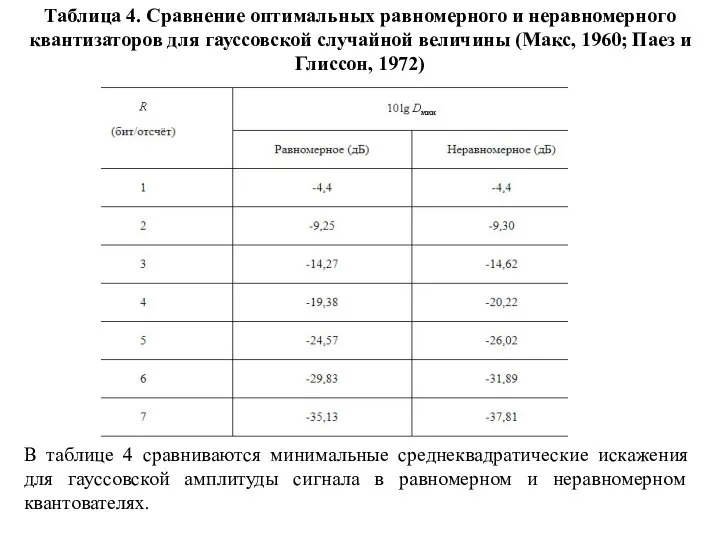
- 136. Таблица 4. Сравнение оптимальных равномерного и неравномерного квантизаторов для гауссовской случайной величины (Макс, 1960; Паез и
- 137. Поучительно построить кривые зависимости минимальных искажений от битовой скорости R=log2L бит на отсчёт (на символ) источника
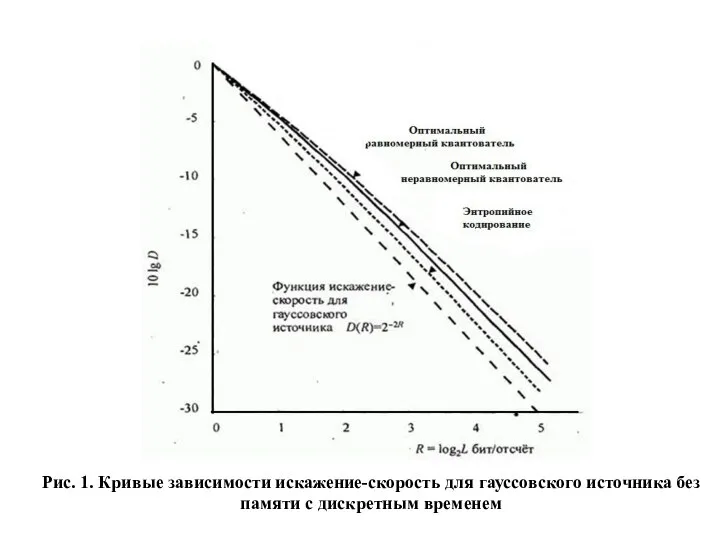
- 138. Рис. 1. Кривые зависимости искажение-скорость для гауссовского источника без памяти с дискретным временем
- 139. Для примера: оптимальный четырёхуровневый неравномерный квантователь для распределённой по Гауссу амплитуды приводит к вероятностям p1=p4=0,1635 для
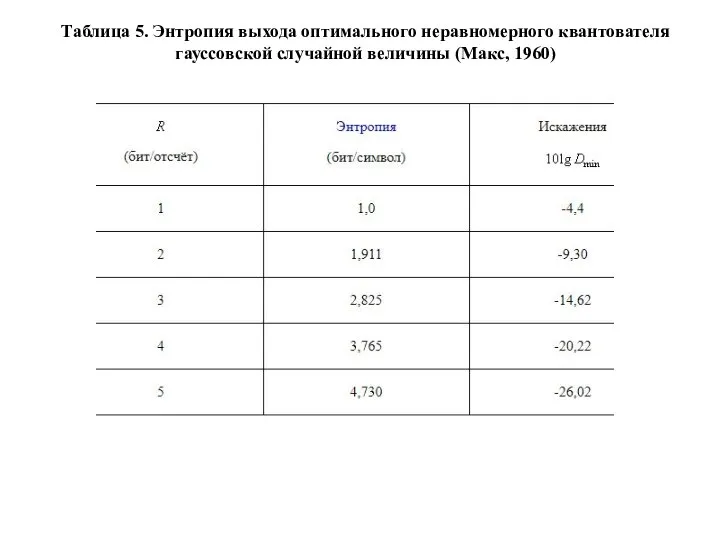
- 140. Таблица 5. Энтропия выхода оптимального неравномерного квантователя гауссовской случайной величины (Макс, 1960)
- 141. Из этого обсуждения мы заключаем, что качество квантователя можно анализировать, когда известна ФПВ непрерывного выхода источника.
- 142. Дискретные выходы квантователя характеризуются рядом вероятностей {pk}, которые можно использовать для расчёта эффективных неравномерных кодов для
- 143. Если мы сравним характеристики оптимального неравномерного квантователя с функцией искажение-скорость, мы найдём, например, что для искажения
- 144. Тема: Векторное представление сообщений и сигналов. Теория построения инфокоммуникационных систем и сетей
- 145. В современной теории передачи информации для описания, анализа и преобразования сообщений и сигналов широко используется геометрическое
- 146. Для определения расстояния между элементами пространства используют некоторый функционал d, который обычно берется таким, чтобы удовлетворялись
- 147. Сигналы можно алгебраически суммировать друг с другом. При этом результатом сложения является также сигнал. Сигналы можно
- 148. 4. Любой элемент пространства можно умножить на любой элемент, принадлежащий скалярному множеству ,на котором определены операции
- 149. Векторное пространство определяет простые алгебраические взаимосвязи между своими элементами. В частности, любой сигнала как вектор может
- 150. Любой сигнал можно описать действительной или комплексной функцией, определенной на интервале , который может быть и
- 151. Для N-мерного линейного пространства действительных или комплексных чисел , j = 1, 2,…, норма определяется как
- 152. Для N-мерного линейного пространства действительных или комплексных чисел с учетом (3) и(5) , (6) а для
- 153. В линейном пространстве можно ввести понятие скалярного произведения двух элементов, которое весьма полезно при рассматривании линейных
- 154. В функциональном анализе доказывается, что в пространстве со скалярным произведением можно ввести норму, удовлетворяющую соотношению ,
- 155. Векторное представление применимо как для детерминированных функций, так и для случайных. В последнем случае скалярные произведения
- 156. Тема: Дискретизация непрерывных сообщений с учетом их характеристик и реальных способов восстановления. Теория построения инфокоммуникационных систем
- 157. Под дискретизацией понимается процесс представления непрерывного сообщения , заданного на интервале ,совокупностью координат . В общем
- 158. При линейных процессах представления и восстановления выражения (1) и (2) можно представить в виде (3) (4)
- 159. В данном случае используется система весовых функций , , где – дельта-функция. При этом, как это
- 160. Для модели сообщения с ограниченным спектром решение указанных задач содержится в теореме Котельникова, на основании которой
- 161. Они образуют ортогональную на бесконечном интервале Систему функций. Любую функцию можно получить на выходе идеального фильтра
- 162. Теорему Котельникова можно распространить и на случайный сигнал. Тогда она формулируется следующим образом: для случайного процесса
- 163. Теорема Котельникова дает предельные соотношения для идеализированных условий, среди которых следует отметить ограниченность спектра по частоте
- 164. Ограничение спектра сообщения частотой путем фильтрации приводит к погрешности восстановления, относительный средний квадрат которой (7) т.
- 165. т. е. она представляет собой с точностью до несущественного множителя сумму бесконечного числа «копий» спектра исходного
- 166. При восстановлении сообщения идеальным фильтром нижних частот с полосой пропускания возникает ошибка, относительный квадрат которой с
- 167. При этом (10) и, следовательно, предварительная фильтрация сообщения с целью ограничения его спектра является целесообразной. Заметим,
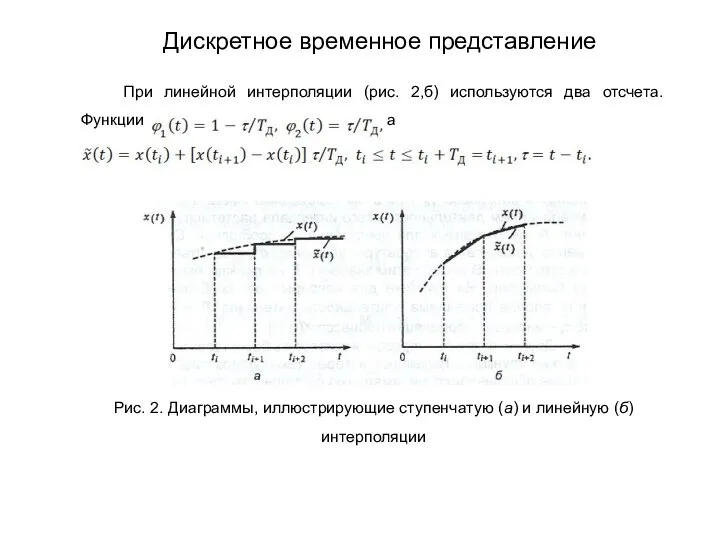
- 168. При линейной интерполяции (рис. 2,б) используются два отсчета. Функции а Рис. 2. Диаграммы, иллюстрирующие ступенчатую (а)
- 169. Относительный средний квадрат погрешности интерполяции зависит от нормированной корреляционной функции исходного процесса , способа интерполяции и
- 170. При заданной погрешности интерполяции формы (11) и (12) используется для нахождения частоты дискретизации. Расчеты показывают, что
- 171. В данном случае координаты сообщения в (3) представляют собой коэффициенты некоторого ряда. При решении рассматриваемой задачи
- 172. Пусть – случайный процесс с нулевым математическим ожиданием и непрерывной корреляционной функцией Тогда можно показать, что
- 173. Собственные функции являются ортогональными и определяются уравнениями с точностью до постоянного множителя, который можно выбрать таким,
- 174. Выражение (15) позволяет находить число координат N, при котором обеспечивается заданная погрешность дискретного представления. Разложение случайного
- 175. В данном случае в качестве весовых функций используют линейные комбинации дельта-функций: (16) где – число сочетания
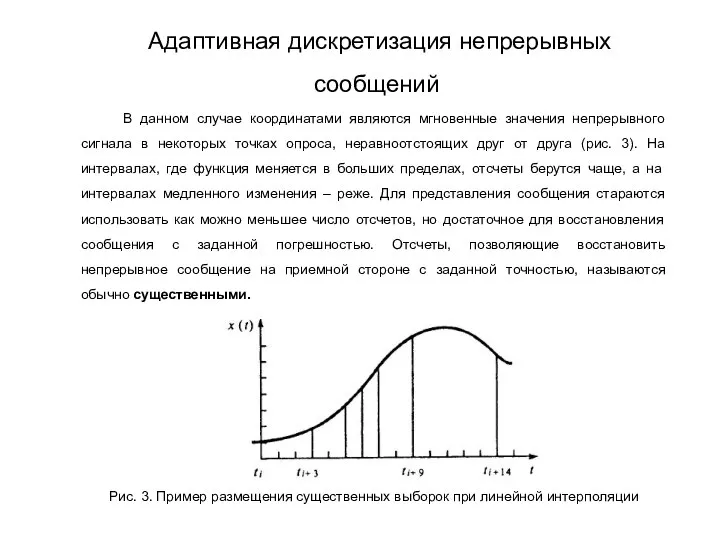
- 176. В данном случае координатами являются мгновенные значения непрерывного сигнала в некоторых точках опроса, неравноотстоящих друг от
- 177. Известны различные способы адаптивной дискретизации, отличающиеся алгоритмом формирования существенных отсчетов и видов служебной информации. Простейшим алгоритм
- 178. При адаптивной дискретизации отсчеты передаются в случайные моменты. Поэтому для восстановления непрерывного сообщения по отсчетам приемная
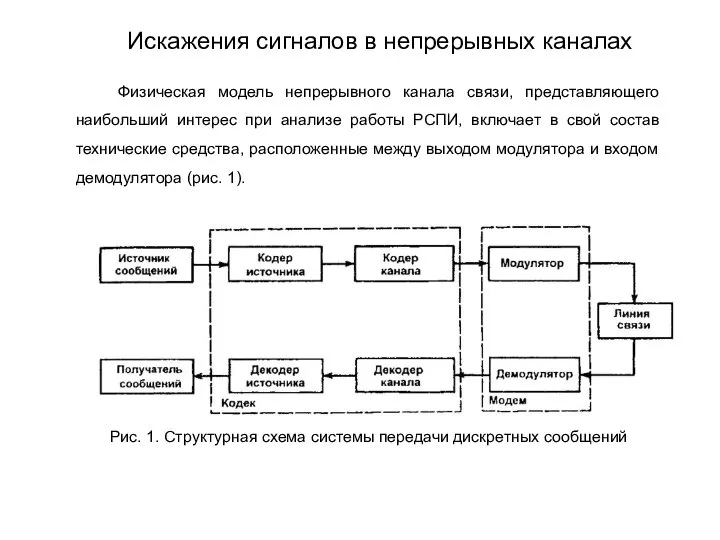
- 179. Физическая модель непрерывного канала связи, представляющего наибольший интерес при анализе работы РСПИ, включает в свой состав
- 180. Проходя по непрерывному каналу связи, сигнал претерпевает ряд изменений. Эти изменения сводятся к ослаблению, искажению сигнала
- 181. Рис. 2. Модель непрерывного канала связи Искажения сигналов в непрерывных каналах
- 182. Линейные искажения проявляются в изменении спектра (корреляционной функции) сигналов и помех. В зависимости от того, каковы
- 183. Характер рассеяния сигнала определяется диапазоном используемых частот и типом системы. Если раньше типичными каналами с рассеянием
- 184. Пусть в точку приема приходят сигналы, переотраженные от совокупности бесконечно малых по размеру отражателей, размещенных в
- 185. фазу, изменяющиеся соответственно по рэлеевскому и равномерному законам. Скорость изменения (ширина спектра флуктуации или время корреляции)
- 186. В общем случае сигнал на выходе линейного канала с изменяющимися параметрами можно найти, используя интеграл Дюамеля
- 187. Фурье и т.п. Если полоса частот сигнала, передаваемого по каналу, ограничена интервалом то достаточно рассматривать функцию
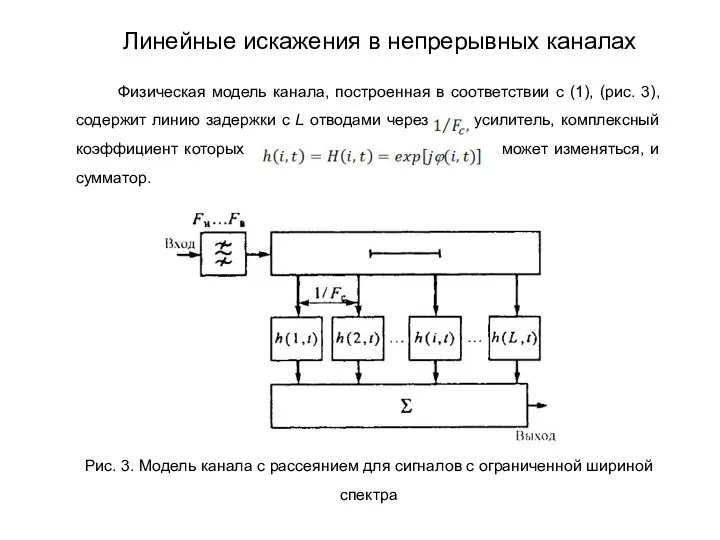
- 188. Физическая модель канала, построенная в соответствии с (1), (рис. 3), содержит линию задержки с L отводами
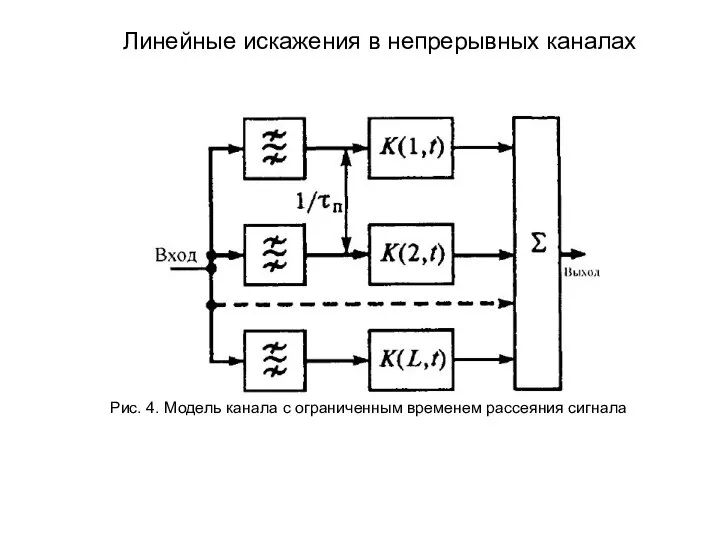
- 189. В частотной области модель канала можно построить в предложении конечности времени рассеяния сигнала. Тогда функция по
- 190. Рис. 4. Модель канала с ограниченным временем рассеяния сигнала Линейные искажения в непрерывных каналах
- 191. Важно знать характер изменения комплексных коэффициентов передачи и в каждой ветви. Если рассеивающий объем состоит из
- 192. Время корреляции или ширина спектра флуктуации характеризуют скорость изменения параметров канала. Например, для КВ канала ширина
- 193. Тема: Модели дискретно-непрерывных каналов. Теория построения инфокоммуникационных систем и сетей
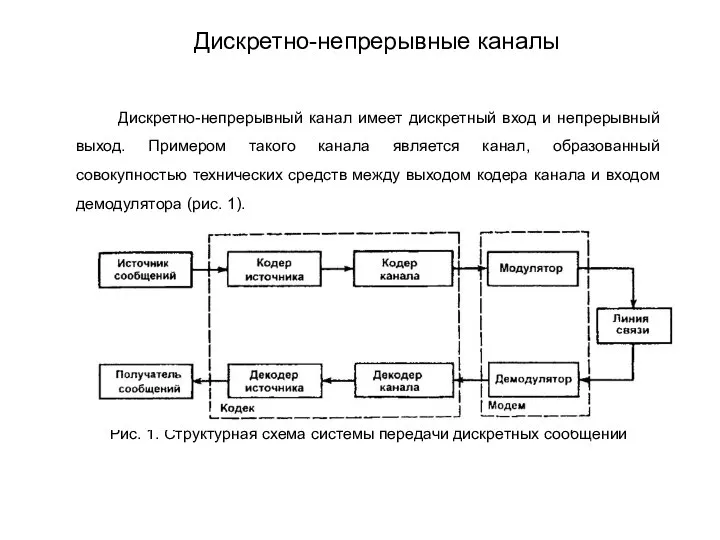
- 194. Дискретно-непрерывный канал имеет дискретный вход и непрерывный выход. Примером такого канала является канал, образованный совокупностью технических
- 195. Для его описания необходимо знать алфавит входных символов вероятность появления символов алфавита полосу пропускания непрерывного канала
- 196. Ширина спектра сигнала не может превышать значение Поэтому В соответствии с теоремой Котельникова его можно представить
- 197. При независимых отсчетах шума Если плотность вероятности для любого сочетания и не зависимы от времени, то
- 198. Тема: Модели непрерывных каналов связи. Теория построения инфокоммуникационных систем и сетей
- 199. Искажения сигналов и помехи в реальных каналах связи весьма многообразны. Тем не менее математическая канала должна
- 200. Канал с гауссовским белым шумом представляет собой идеальный канал, в котором на сигнал накладывается помеха Коэффициент
- 201. Гауссовский канал с неопределенной амплитудой и фазой сигнала вносит в сигнал наряду с флуктуациями фазы и
- 202. В радиосистемах передачи дискретной информации, когда время памяти канала соизмеримо с длительностью посылки (а тем более
- 203. Возможно дальнейшее усложнение модели с нелинейными искажениями, если предположить наличие в канале еще и линейных искажений,
- 204. Тема: Нелинейные искажения в каналах связи. Теория построения инфокоммуникационных систем и сетей
- 205. Нелинейные искажения возникают в результате прохождения сигнала по звеньям с нелинейной амплитудной характеристикой . Так как
- 206. Так как приемное устройство обычно содержит на входе полосовой фильтр, пропускающий только спектральные составляющие в области
- 207. Картина искажения сигнала существенно усложняется, когда одновременно с полезным сигналом действуют другие сигналы или помехи. В
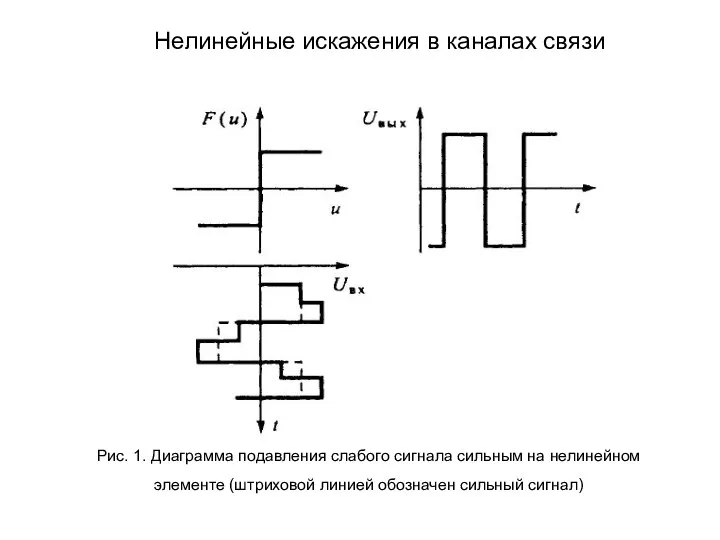
- 208. Особый интерес как нелинейность представляет так называемый предельный ограничитель, для которого . Пусть на его входе
- 209. Рис. 1. Диаграмма подавления слабого сигнала сильным на нелинейном элементе (штриховой линией обозначен сильный сигнал) Нелинейные
- 210. Для помехи, представляющей собой сумму гармонического сигнала и гауссовской помехи, коэффициент подавления полезного сигнала можно рассчитать
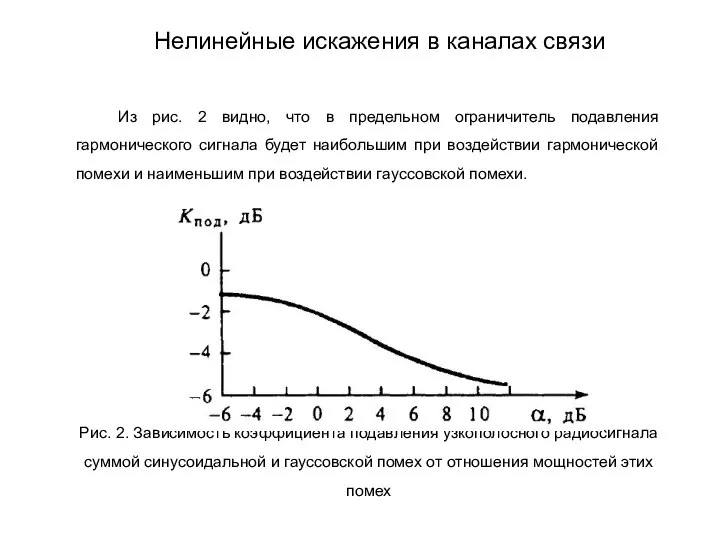
- 211. Из рис. 2 видно, что в предельном ограничитель подавления гармонического сигнала будет наибольшим при воздействии гармонической
- 212. Тема: Неравномерное квантование. Теория построения инфокоммуникационных систем и сетей
- 213. Неравномерное квантование, хотя и сложнее в реализации, чем равномерное, довольно часто используется при передаче речевых сигналов.
- 214. Неравномерное квантование можно реализовать различными способами, например квантованием с соответствующей амплитудной характеристикой (непосредственное неравномерное квантование). При
- 215. Неравномерное квантование можно реализовать различными способами, например квантованием с соответствующей амплитудной характеристикой (непосредственное неравномерное квантование). При
- 216. Рис. 1. Структурная схема компандирования При неравномерном квантовании дисперсия погрешности квантования (1) где и – нижняя
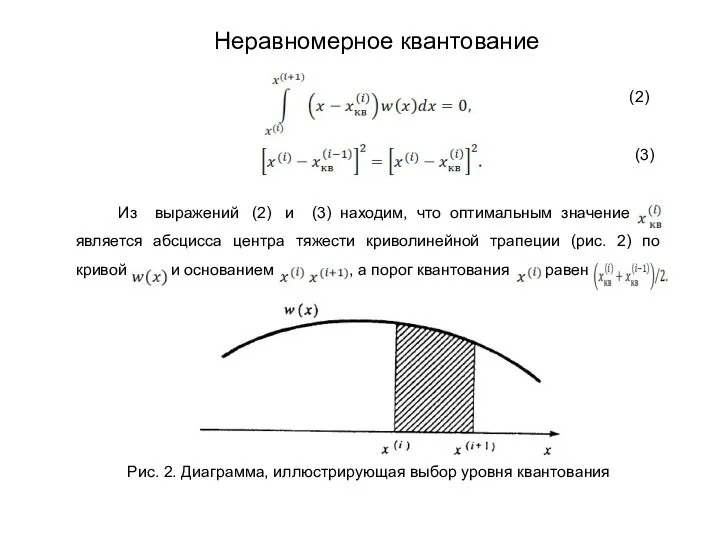
- 217. (2) (3) Из выражений (2) и (3) находим, что оптимальным значение является абсцисса центра тяжести криволинейной
- 218. В частности, из (2) и (3) нетрудно видеть, что если распределение Равномерное, то квантование с постоянным
- 219. Двоичный натуральный код – это код, комбинации которого представляют собой двоичные номера уровней квантования. Он прост
- 220. Код Грея связан с двоичным натуральным кодом следующими соотношениями: где – кодовая комбинация натурального кода, –
- 221. Рассмотренные коды обеспечивают одинаковую погрешность восстановления из-за ошибок в канале связи при условии, что ошибки возникают
- 222. Тема: Общие сведения о каналах связи. Теория построения инфокоммуникационных систем и сетей
- 223. Каналы связи можно классифицировать по различным показателям. В теории передачи сигналов каналы классифицируются по характеру сигналов
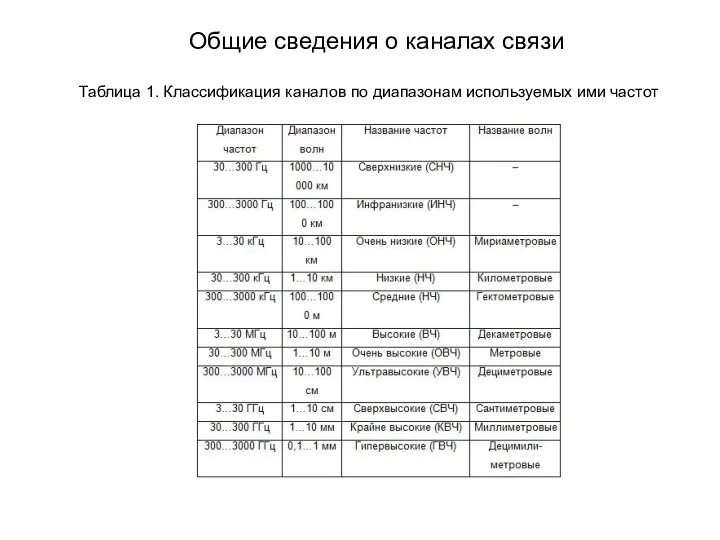
- 224. Таблица 1. Классификация каналов по диапазонам используемых ими частот Общие сведения о каналах связи
- 225. По способу распространения радиоволн различают каналы с открытым и с закрытым распространением. В каналах с закрытым
- 226. стабильностью. Особенностью этих диапазонов является также способность волн проникать в толщу Земли и воды на глубину
- 227. проникновения в ионосферу зависит от длины волны, то для передачи информации между двумя пунктами можно указать
- 228. дальних радионавигации. Гектометровые волны днем распространяются как земные, а ночью – как ионосферные. Дальность распространения земной
- 229. сигналов и возможностью использования одинаковых частот для организации связи в зонах, удаленных на расстояния, превышающие радиогоризонт.
- 230. Стремление увеличить дальность радиолинии в этих диапазонах без промежуточной ретрансляции нашел свое решение в РСПИ, использующих
- 231. Новую эру в освоению высокочастотной области радиодиапазона для средств связи открыл запуск искусственных спутников Земли (ИСЗ).
- 232. земной поверхности от одного ИСЗ или, иначе говоря, максимальное расстояние вдоль поверхности Земли между двумя стациями
- 233. спутников, орбиты которых выбраны так, что над любой точкой на поверхности Земли находится по крайней мере
- 234. Тема: Помехи в каналах связи. Теория построения инфокоммуникационных систем и сетей
- 235. Ошибки, возникающие при приеме сообщения, в значительной степени определяются видом и интенсивностью помех, действующих в канале.
- 236. Различают тепловой и дробовый шумы. Тепловой шум обусловлен тепловым движением носителей заряда, приводящим к появлению случайной
- 237. Шумы электровакуумных и полупроводниковых приборов (дробовые шумы) обусловлены дискретной природой носителей заряда. Статистические характеристики дробового шума
- 238. Атмосферные помехи возникают в результате различных электрических процессов, происходящих в земной атмосфере. Наиболее мощными источником является
- 239. Земная поверхность, как и всякое нагретое тело, излучает электромагнитные волны. Они могут попадать в антенну по
- 240. Одним из распространенных видов помех являются помехи от посторонних радиостанций. Насыщенность радиосредствами (радиосвязь, радиолокация, радионавигация и
- 241. Станционные помехи присутствуют практически во всех диапазонах, и особенно в коротковолновом, где из-за ионосферного распространения радиоволн
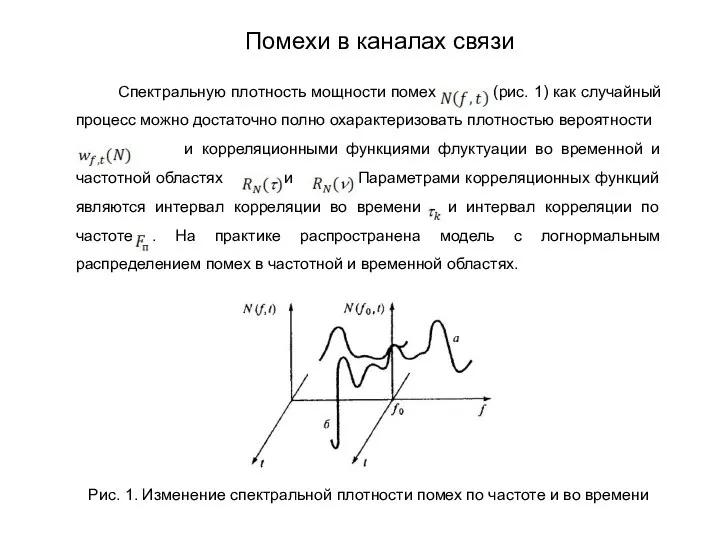
- 242. Спектральную плотность мощности помех (рис. 1) как случайный процесс можно достаточно полно охарактеризовать плотностью вероятности и
- 243. Если число стационарных помех, попадающих в полосу сигнала, ограничено, то рассмотренная модель не всегда применима. В
- 244. Тема: Преобразование непрерывных сообщений в цифровую форму. Операция квантования по уровню. Теория построения инфокоммуникационных систем и
- 245. Непрерывные сообщения можно передавать по дискретным системам связи. Для этого их преобразуют в цифровую форму (в
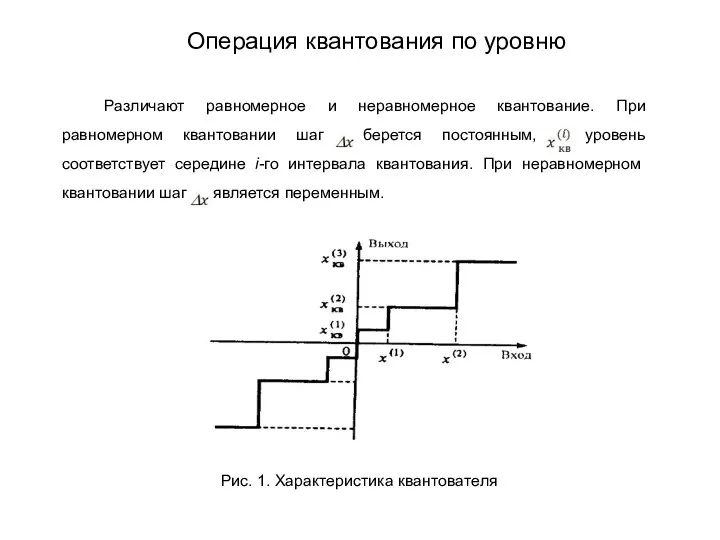
- 246. Различают равномерное и неравномерное квантование. При равномерном квантовании шаг берется постоянным, а уровень соответствует середине i-го
- 247. Замена непрерывного множества возможных значений сообщения дискретным множеством фиксированных значений приводит к погрешности, называемой шумом квантования.
- 248. Таким образом, для рассматриваемого случая дисперсия погрешности равномерного квантования зависит только от значения шага или при
- 326. Скачать презентацию











































![когда L равно целой степени основания 2, и R=[log2 L]+1 когда](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/753496/slide-46.jpg)
































































































































































































































































 Проектирование. Акватории расположения морских платформ
Проектирование. Акватории расположения морских платформ Национальные костюмы
Национальные костюмы Программное и аппаратное прерывание
Программное и аппаратное прерывание Газовая турбина
Газовая турбина ?????????????????
????????????????? Асинхронный двигатель
Асинхронный двигатель 20140209_sluzhba_v_armii
20140209_sluzhba_v_armii 20140414_urok_po_teme_poznanie_i_soznanie
20140414_urok_po_teme_poznanie_i_soznanie 20160309_n.a._nekrasov_-_nachalo
20160309_n.a._nekrasov_-_nachalo Организация работы службы документационного обеспечения
Организация работы службы документационного обеспечения Center for Social and Psychological Support of Students MarSU
Center for Social and Psychological Support of Students MarSU Виды полиграфической продукции
Виды полиграфической продукции Российская Академия Наук
Российская Академия Наук Птицы собираются в стаи
Птицы собираются в стаи Понятие о размерах зоны основания сооружений
Понятие о размерах зоны основания сооружений Молочные породы коров
Молочные породы коров Село Бурабай
Село Бурабай Визуальный и измерительный контроль
Визуальный и измерительный контроль Красота слова
Красота слова 88-й рейс НИС Академик Мстислав Келдыш
88-й рейс НИС Академик Мстислав Келдыш Балашов Максим Игоревич
Балашов Максим Игоревич Обзор новых скверов г. Уфы
Обзор новых скверов г. Уфы Нам в этот день рожден Спаситель
Нам в этот день рожден Спаситель Тест по теме Пайка металлов
Тест по теме Пайка металлов 20171116_sochetaniya_bez_povtoreniy
20171116_sochetaniya_bez_povtoreniy Многокомпонентные цементы на основе портландцементного клинкера
Многокомпонентные цементы на основе портландцементного клинкера Маленькие открытия в моей большой семье
Маленькие открытия в моей большой семье Проверь себя и пройди тест
Проверь себя и пройди тест