Содержание
- 2. Задача о минимаксном остове взвешенного графа
- 3. На взвешенном неориентированном графе G(X,U) требуется выделить подмножество ребер U’ таких, что: 1. Отношения достижимости вершин
- 4. Требуется выбрать такие маршруты передвижения между населенными пунктами, которые бы обеспечивали перевозку максимального количества товара каждым
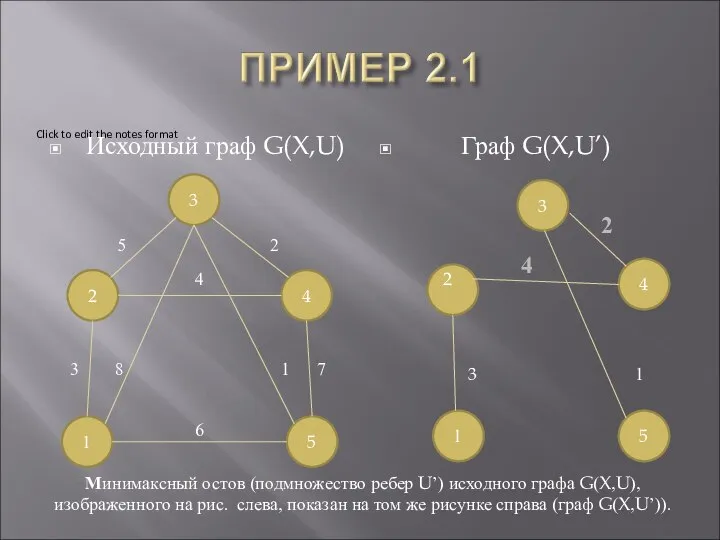
- 5. Исходный граф G(X,U) Граф G(X,U’) 4 1 2 3 4 5 3 8 1 7 5
- 7. Шаг 1. А = 1 Шаг 2. В = │U│. Шаг 3. Ищется перестановка ребер π
- 8. Пользуясь приведенным выше алгоритмом, определить минимаксный остов графа, изображенного на рис. 2.1 слева. Решение. А=1. В=8.
- 9. 10. Очевидно, что отношения достижимости вершин графов G(X,U’) и G(X,U) не совпадают. 11. А = С
- 10. Достоинства: Гарантия получения глобально оптимального решения. Сравнительно высокое быстродействие. Легкость программной реализации. Возможность использовать алгоритм для
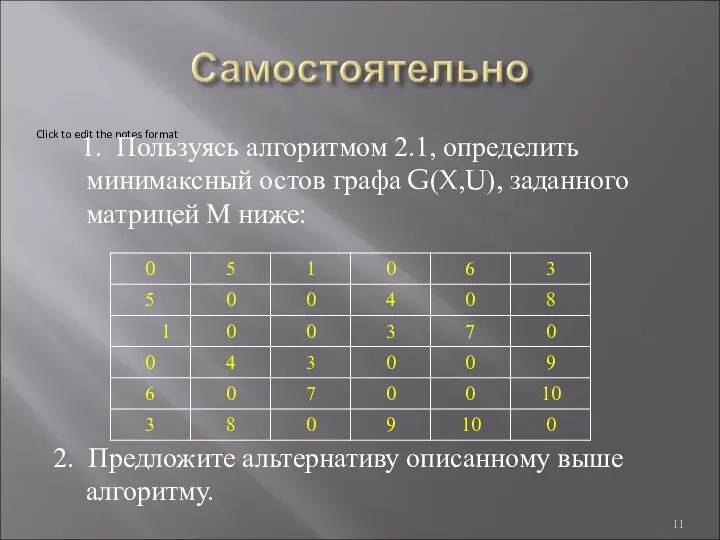
- 11. 1. Пользуясь алгоритмом 2.1, определить минимаксный остов графа G(X,U), заданного матрицей М ниже: 2. Предложите альтернативу
- 12. Задача о минимаксных маршрутах
- 13. На взвешенном неориентированном графе G(X,U) выделена вершина и требуется определить такое подмножество ребер U’, что: 1.
- 14. Требуется выбрать такие маршруты передвижения между населенными пунктами, которые бы обеспечивали перевозку максимального количества товара каждым
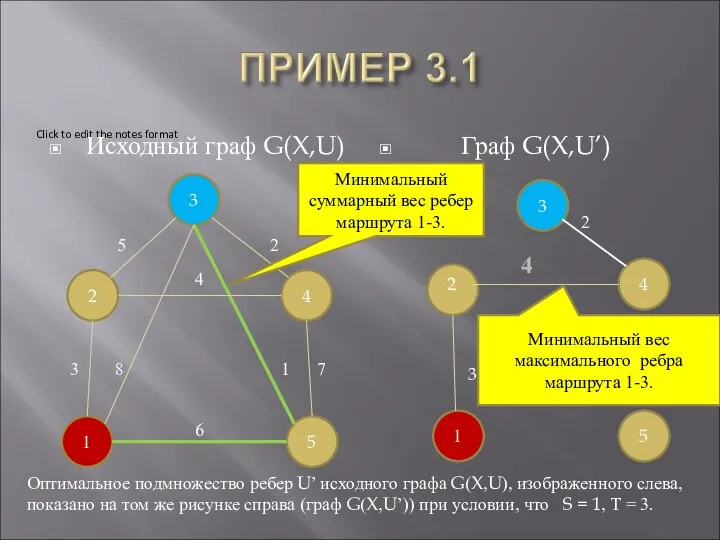
- 15. Исходный граф G(X,U) Граф G(X,U’) 4 1 2 3 4 5 3 8 1 7 5
- 17. Шаг 1. Q = 0. Шаг 2. На множестве ребер, инцидентных выделенной вершине , выбирается ребро
- 18. Пользуясь приведенным выше алгоритмом 3.1, определить оптимальное значение целевой функции задачи (3.1) применительно к графу, изображенному
- 19. Q = 0. Выбирается ребро (1,2), вес которого равен трем, Q=3. Вес всех ребер, инцидентных х₁,
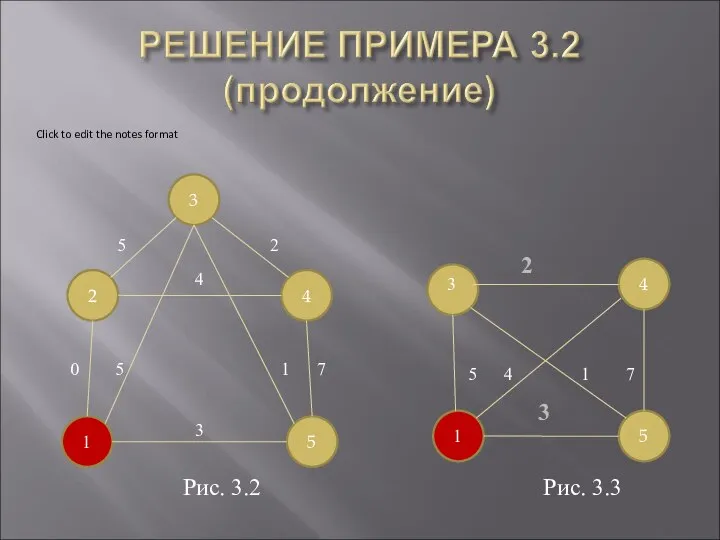
- 20. 2 1 2 3 4 5 0 5 1 7 5 2 4 3 1 3
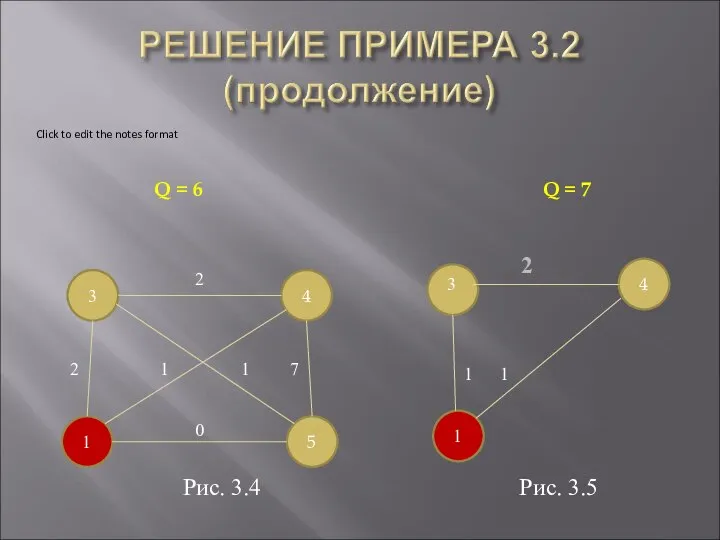
- 21. 5. Выбирается ребро (1,5) с весом, равным трем. 6. Q=Q+3=6. 7. Вес всех ребер, инцидентных х₁,
- 22. 2 1 3 4 5 2 1 1 7 2 0 1 3 4 1 1
- 23. 10. Вес обоих ребер, инцидентных первой вершине, равен единице. 11. Q = Q + 1 =
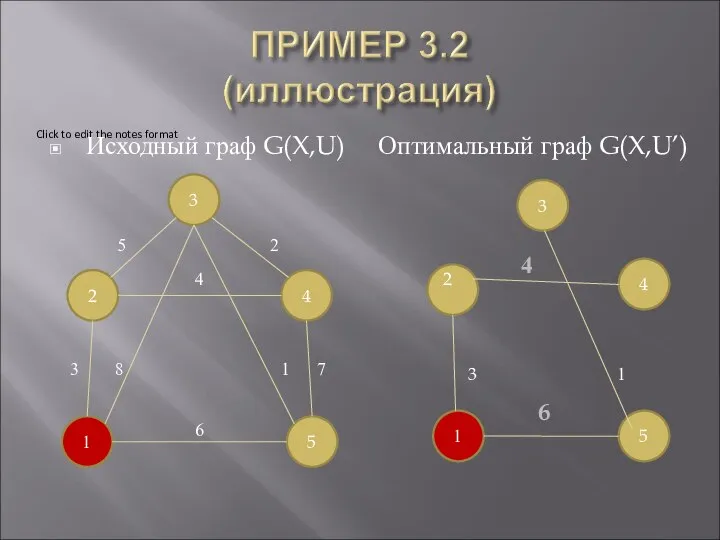
- 24. Исходный граф G(X,U) Оптимальный граф G(X,U’) 4 1 2 3 4 5 3 8 1 7
- 25. Достоинства: Гарантия получения глобально оптимального решения. Высокое быстродействие. Легкость программной реализации. Низкие требования к объему оперативной
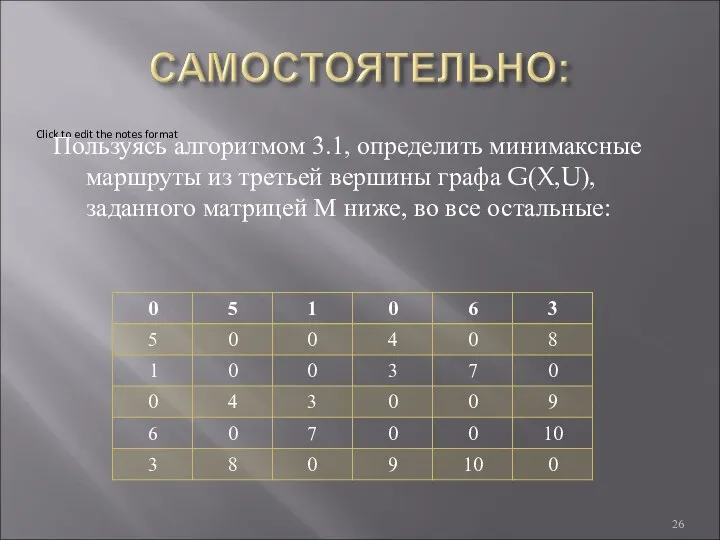
- 26. Пользуясь алгоритмом 3.1, определить минимаксные маршруты из третьей вершины графа G(X,U), заданного матрицей М ниже, во
- 27. Определить: минимаксные маршруты из второй вершины графа G(X,U), заданного матрицей М ниже, во все остальные: минимальные
- 28. №3 №4
- 30. №7 №8
- 31. №9 №10
- 32. №11 №12
- 33. №13 №14
- 34. №15 №16
- 35. №17 №18
- 36. №19 №20
- 37. №21 №22
- 39. Скачать презентацию





























 Работа с бумагой. Бабочки
Работа с бумагой. Бабочки Onomastyka przedmiot i działy. Toponomastyka klasyfikacja nazw miejscowych. (Wykład 6)
Onomastyka przedmiot i działy. Toponomastyka klasyfikacja nazw miejscowych. (Wykład 6) Каменные стражи СПБ
Каменные стражи СПБ compare and contrast photos
compare and contrast photos Санаторий Самшитовая Роща
Санаторий Самшитовая Роща Построение параллелограмма
Построение параллелограмма Основные сведения о сварке, сварочная дуга, способы сварки
Основные сведения о сварке, сварочная дуга, способы сварки конденсатор
конденсатор Технология сварки упрочненных сталей. Билет 11 (1)
Технология сварки упрочненных сталей. Билет 11 (1) День заповедников и национальных парков ( подготовительная группа)
День заповедников и национальных парков ( подготовительная группа) General Motors — крупнейшая американская автомобильная корпорация
General Motors — крупнейшая американская автомобильная корпорация Религия и повседневность
Религия и повседневность Лучший казачий кадетский корпус Уральского Федерального округа
Лучший казачий кадетский корпус Уральского Федерального округа Игра. Сделка
Игра. Сделка 20151008_avangardizm
20151008_avangardizm Зразки_заготовок_до_першого_уроку_2
Зразки_заготовок_до_першого_уроку_2 Подготовка поверхностей под облицовку
Подготовка поверхностей под облицовку ООО Делмакс. Приглашает инвесторов к совместной реализации проектов производств и логистического центра
ООО Делмакс. Приглашает инвесторов к совместной реализации проектов производств и логистического центра Твердотельная электроника. Семинар №7. Расчет характеристик МОПТ в рамках идеальной модели
Твердотельная электроника. Семинар №7. Расчет характеристик МОПТ в рамках идеальной модели 20130217_otkrytyy_urok-italiya
20130217_otkrytyy_urok-italiya Католицизм. Урок 12
Католицизм. Урок 12 Уравнение обмена
Уравнение обмена Исполнители вокруг нас
Исполнители вокруг нас для школьник
для школьник вводное занятие по дисциплине Обществознание
вводное занятие по дисциплине Обществознание Мы рядом с вами. Особенные дети в обычной школе
Мы рядом с вами. Особенные дети в обычной школе Xayrullayeva Dinora Shuxratovna YOZGI
Xayrullayeva Dinora Shuxratovna YOZGI 1 урок
1 урок