Содержание
- 2. Теория оптимизации: основные понятия Классические задачи оптимизации на графах: задача о минимальном (максимальном) покрывающем дереве в
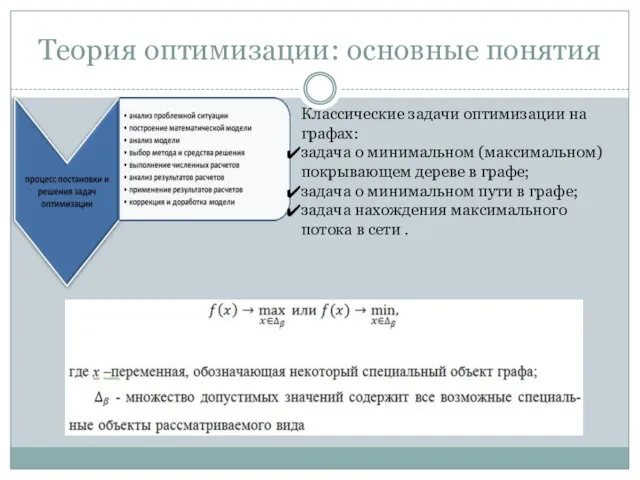
- 3. Задача о минимальном покрывающем дереве в графе: постановка задачи Стоимость прокладки автодороги между двумя соседними населенными
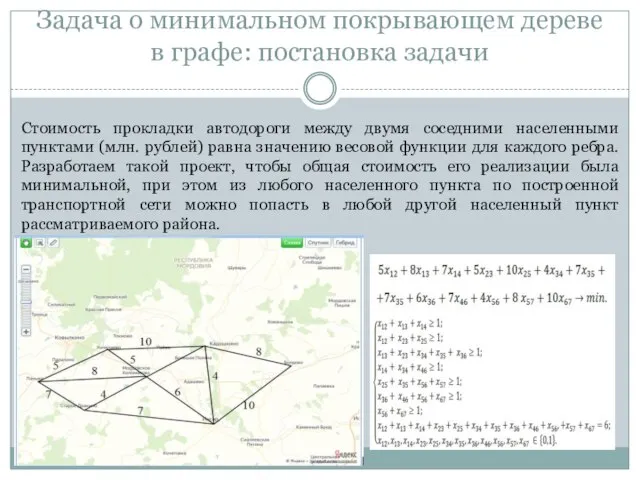
- 4. Задача о минимальном покрывающем дереве в графе: решение задачи в Ms Excel Таблица с исходными данными
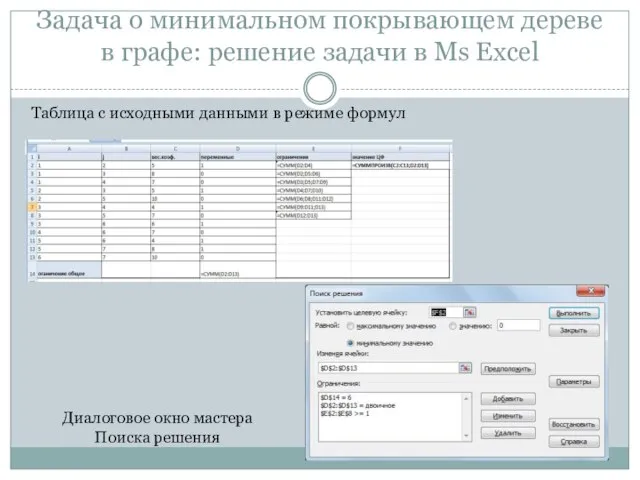
- 5. Задача о минимальном покрывающем дереве в графе: результат решение задачи оптимальный проект транспортной сети рассматриваемого района
- 6. Задача о минимальном пути в графе Дана схема железнодорожной сети в виде графа. Протяженность каждой дороги
- 7. Задача о минимальном пути в графе
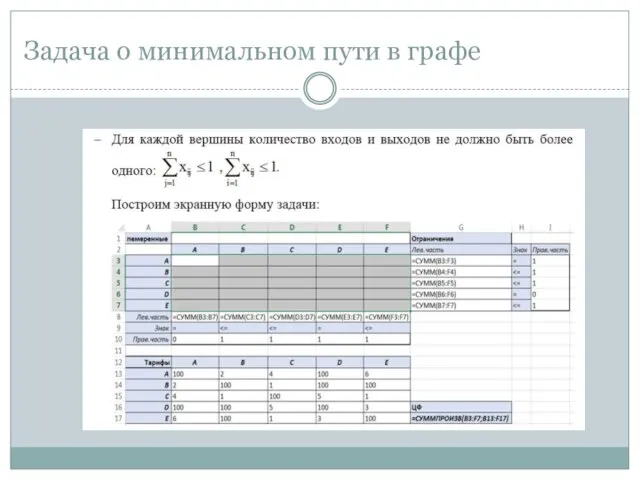
- 8. Задача о минимальном пути в графе
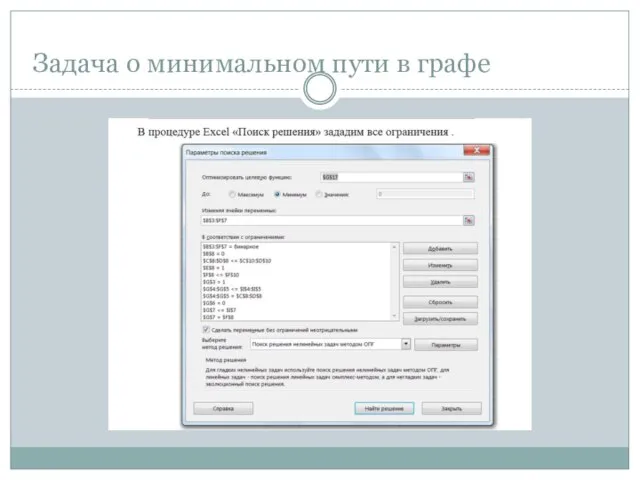
- 9. Задача о минимальном пути в графе
- 11. Скачать презентацию


 Возвратные карты. ТЗ
Возвратные карты. ТЗ Свадебный бум
Свадебный бум Технологии регистрации заряженных частиц, сбор и анализ данных детекторов в ФВЭ. ATLAS. (Лекция 4)
Технологии регистрации заряженных частиц, сбор и анализ данных детекторов в ФВЭ. ATLAS. (Лекция 4) 20150624_6_klass_viktorina_1_zadachi_na_uravneniya
20150624_6_klass_viktorina_1_zadachi_na_uravneniya прописи 5-7 лет
прописи 5-7 лет Способы обеспечения точности сборки
Способы обеспечения точности сборки Фотоальбом. Строительство
Фотоальбом. Строительство Система топливного, пускового и импульсного газа
Система топливного, пускового и импульсного газа Программа элективного курса Средства связи (для 9 классов)
Программа элективного курса Средства связи (для 9 классов) План
План Морская промежуточная вертолетная платформа. Технические предложения
Морская промежуточная вертолетная платформа. Технические предложения 20150511_professii
20150511_professii Организация обучения по окружающему миру. Принципы отбора содержания и составления дистанционного урока
Организация обучения по окружающему миру. Принципы отбора содержания и составления дистанционного урока Требования к изучению специальных дисциплин по направлениям и профилям бакалавриата и магистратуры
Требования к изучению специальных дисциплин по направлениям и профилям бакалавриата и магистратуры Жизненный путь Зайцева Михаила Петровича
Жизненный путь Зайцева Михаила Петровича Моторы и датчики EV3
Моторы и датчики EV3 Демо продажи(установление контакта)
Демо продажи(установление контакта) 011_plosk_zakrep
011_plosk_zakrep Назначение, устройство и принцип работы основных элементов ГТУ. Лекция №2.2
Назначение, устройство и принцип работы основных элементов ГТУ. Лекция №2.2 1 стр. обложки
1 стр. обложки программирование
программирование XX Межпредметная олимпиада Русский музей во дворцах и в Интернете
XX Межпредметная олимпиада Русский музей во дворцах и в Интернете 20151213_pamyatki_po_istorii_i_obshchestvoznaniyu_
20151213_pamyatki_po_istorii_i_obshchestvoznaniyu_ ТАНГРАМ
ТАНГРАМ Елена Коренская. Архитектор-дизайнер
Елена Коренская. Архитектор-дизайнер Повышение эффективности перекачки нефти Ванкорского месторождения по второй нитке магистрального нефтепровода Пурпе - Самотлор
Повышение эффективности перекачки нефти Ванкорского месторождения по второй нитке магистрального нефтепровода Пурпе - Самотлор Банк Бор (15.11.2016) — с пометками для расчета
Банк Бор (15.11.2016) — с пометками для расчета Пластилиновые узоры
Пластилиновые узоры