Содержание
- 2. Содержание Понятие числовой последовательности Примеры числовых последовательностей Способы задания последовательностей Ограниченность числовых последовательностей Возрастание и убывание
- 3. Понятие числовой последовательности Рассмотрим ряд натуральных чисел N: 1, 2, 3, …, n – 1, n,
- 4. Примеры числовых последовательностей 1, 2, 3, 4, 5, … – ряд натуральных чисел; 2, 4, 6,
- 5. Способы задания последовательностей Перечислением членов последовательности (словесно). Заданием аналитической формулы. Заданием рекуррентной формулы. Примеры: Последовательность простых
- 6. Ограниченность числовой последовательности Последовательность {уn} называют ограниченной сверху, если все ее члены не больше некоторого числа.
- 7. Ограниченность числовой последовательности Последовательность {уn} называют ограниченной снизу, если все ее члены не меньше некоторого числа.
- 8. Возрастание и убывание числовой последовательности Последовательность {уn} называют возрастающей последовательностью, если каждый ее член больше предыдущего:
- 9. Предел числовой последовательности Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении
- 10. Предел числовой последовательности Это определение означает, что a есть предел числовой последовательности, если её общий член
- 11. Рассмотрим последовательность: – гармонический ряд Если │q│ Если │q│> 1, то последовательность уn = q n
- 12. Свойства пределов предел частного равен частному пределов: предел произведения равен произведению пределов: предел суммы равен сумме
- 13. Примеры:
- 14. Если mN, kR, то
- 15. Сумма бесконечной геометрической прогрессии Пример: Дано: b1 + b2 + b3 + b4 + … +
- 16. Предел функции на бесконечности В этом случае прямая у = b является горизонтальной асимптотой графика функции
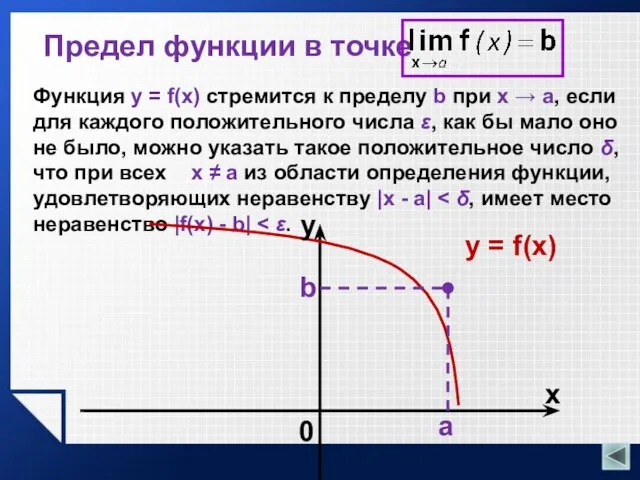
- 17. Предел функции в точке Функция y = f(x) стремится к пределу b при x → a,
- 19. Скачать презентацию















 Комбинационные асинхронные устройства
Комбинационные асинхронные устройства What are they saying
What are they saying Роль исламского образования и духовного воспитания в формировании религиозной идентичности детей
Роль исламского образования и духовного воспитания в формировании религиозной идентичности детей Давня Спарта. Спартанська культура. Побут спартанців
Давня Спарта. Спартанська культура. Побут спартанців Мониторинг закупок, аудит и контроль в сфере закупок
Мониторинг закупок, аудит и контроль в сфере закупок Тема 7. Учёт собственного капитала предприятия В состав собственного капитала включаются: уставный капитал, добавочный капитал, резервы, нераспределённая прибыль прошлых лет, прибыль отчетного периода, неосновной капитал. Уставный капитал представ
Тема 7. Учёт собственного капитала предприятия В состав собственного капитала включаются: уставный капитал, добавочный капитал, резервы, нераспределённая прибыль прошлых лет, прибыль отчетного периода, неосновной капитал. Уставный капитал представ Воспитание младших школьников на краеведческом материале (Из опыта работы Ослоповских Г.Н.) Любить свой край, знать его богатства
Воспитание младших школьников на краеведческом материале (Из опыта работы Ослоповских Г.Н.) Любить свой край, знать его богатства Анализ отраслевых методов идентификации спиртов
Анализ отраслевых методов идентификации спиртов Предмет политологии, место политологии в системе гуманитарных наук
Предмет политологии, место политологии в системе гуманитарных наук Презентация Пушно-меховые товары
Презентация Пушно-меховые товары Использование ИКТ на уроках истории и обществознания при подготовке к ЕГЭ Подготовила: учитель истории и обществознания МОУСОШ 34
Использование ИКТ на уроках истории и обществознания при подготовке к ЕГЭ Подготовила: учитель истории и обществознания МОУСОШ 34 Сервисный тренинг EXD06 Система контроля давления воздуха в шинах (второе поколение)
Сервисный тренинг EXD06 Система контроля давления воздуха в шинах (второе поколение) Политические учения Средневековой Европы
Политические учения Средневековой Европы Обязательные нормативы банков. GFS New Hires training
Обязательные нормативы банков. GFS New Hires training Хохломская роспись
Хохломская роспись Краски древнерусской живописи
Краски древнерусской живописи И.И.Шишкин «Пейзаж с озером»
И.И.Шишкин «Пейзаж с озером» Сказка о царе Салтане - часть 1 - презентация для начальной школы
Сказка о царе Салтане - часть 1 - презентация для начальной школы Washington is the capital of the United States
Washington is the capital of the United States Городецкая роспись по дереву
Городецкая роспись по дереву С праздником весны
С праздником весны Лидер и мир. Что предполагает Евангелие
Лидер и мир. Что предполагает Евангелие Презентация «Организация таможенного контроля товаров и транспортных средств» на тему «Особенности таможенного декларировани
Презентация «Организация таможенного контроля товаров и транспортных средств» на тему «Особенности таможенного декларировани Қазақстан тарихында музыкалық аспаптар
Қазақстан тарихында музыкалық аспаптар Без названия
Без названия Электронные платежные системы в России
Электронные платежные системы в России  «Прямая пропорциональность»
«Прямая пропорциональность»  Презентация "Мода и стили в одежде" - скачать презентации по МХК
Презентация "Мода и стили в одежде" - скачать презентации по МХК