Содержание
- 2. Алгебра высказываний Алгебра высказываний была разработана для того, чтобы определять истинность или ложность составных высказываний, не
- 3. Логические переменные Логические переменные – простые высказывания, содержащие только одну мысль. Обозначаются буквами латинского алфавита: A,
- 4. Логические переменные Например, два простых высказывания: А = «2 × 2 = 4» истина (1) В
- 5. В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: «ИСТИНА» (1)
- 6. В алгебре высказываний над логическими переменными (над высказываниями) можно производить определенные логические операции, в результате которых
- 7. Составные высказывания Высказывания, состоящие из нескольких простых суждений и содержащие в себе более, чем одну простую
- 8. Логические операции Конъюнкция (логическое умножение, «И») Дизъюнкция (логическое сложение, «ИЛИ») Инверсия (логическое отрицание, «НЕ») Импликация (логическое
- 9. Объединение двух или нескольких высказываний в одно с помощью союза «И» называется операцией логического умножения, или
- 10. Логическая функция, полученная в результате конъюнкции, истинна тогда и только тогда, когда истинны все входящие в
- 11. Конъюнкция. Определите истинность логической функции «2 × 2 = 5» И «3 × 3 = 10»
- 12. Запись конъюнкции на формальном языке алгебры высказываний F(A,B) = A & B или F(A,B) = A
- 13. Значение логической функции определяется по ее таблице истинности Таблица истинности показывает какие значения принимает логическая функция
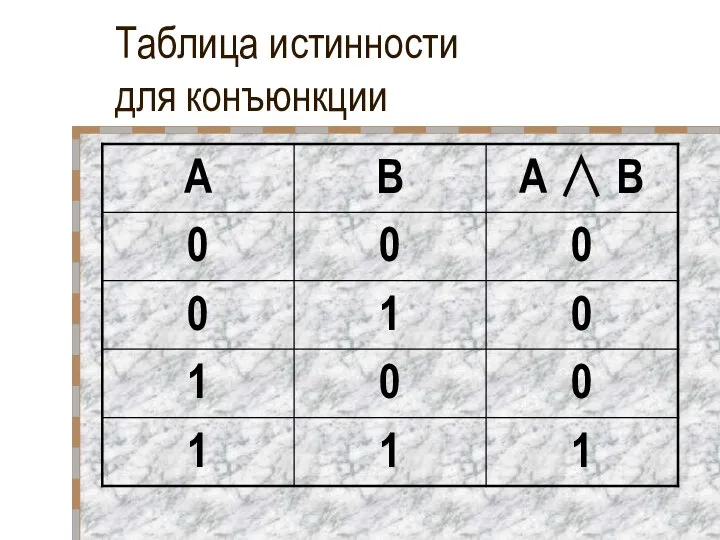
- 14. Таблица истинности для конъюнкции
- 15. Таблица истинности для конъюнкции
- 16. Объединение двух или нескольких высказываний в одно с помощью союза «ИЛИ» называется операцией логического сложения, или
- 17. Логическая функция, полученная в результате дизъюнкции, истинна тогда, когда истинна хотя бы одна из входящих в
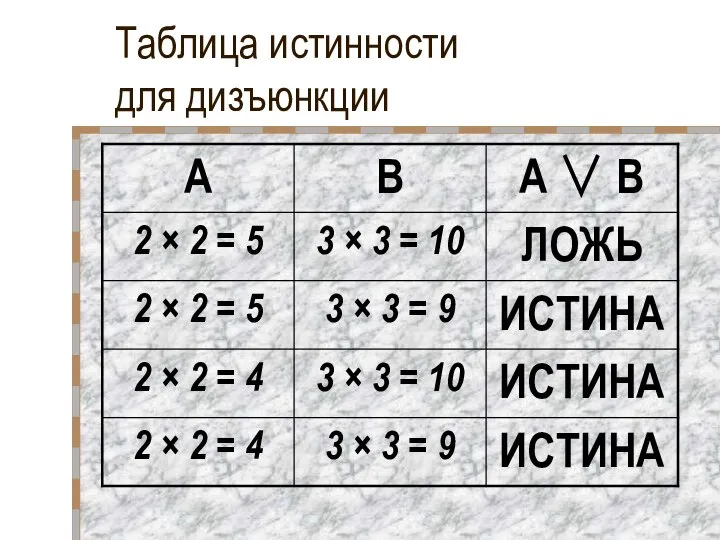
- 18. Дизъюнкция. Определите истинность логической функции «2 × 2 = 5» ИЛИ «3 × 3 = 10»
- 19. Запись дизъюнкции на формальном языке алгебры высказываний F(A,B) = A ∨ B Также может встретиться запись,
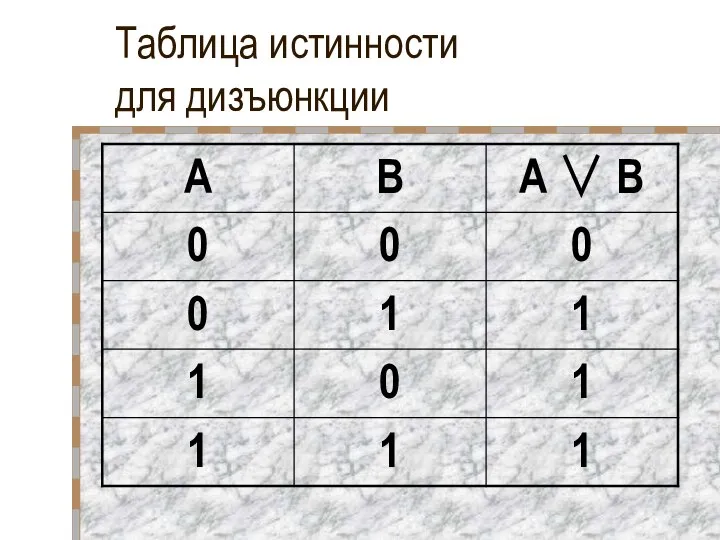
- 20. Таблица истинности для дизъюнкции
- 21. Таблица истинности для дизъюнкции
- 22. Присоединение частицы «НЕ» к высказыванию называется операцией логического отрицания, или инверсией
- 23. Логическое отрицание (инверсия) делает истинное высказывание ложным, а ложное – истинным [логическая отрицательная единица, перевертыш]
- 24. Инверсия Пусть A = «2 × 2 = 4» – истинное высказывание, тогда F(A) = «2
- 25. Запись инверсии на формальном языке алгебры высказываний F(A) = ¬A или F(A) = Ā Также может
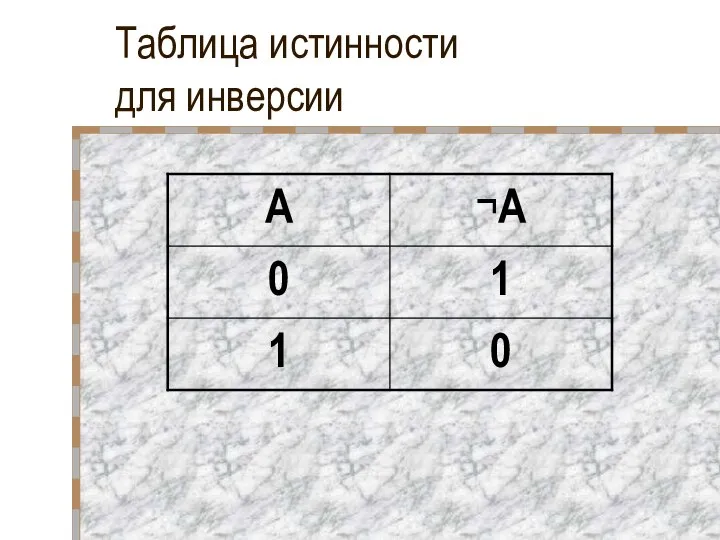
- 26. Таблица истинности для инверсии
- 27. Таблицы истинности основных логических функций Логическое умножение A 0 0 1 1 B 0 1 0
- 28. Дополнительные логические функции Импликацию и эквивалентность можно выразить через конъюнкцию, дизъюнкцию и отрицание, поэтому их называют
- 29. Импликация Объединение двух высказываний, из которых первое является условием, а второе – следствием из него, называется
- 30. Импликация Импликация ложна тогда и только тогда, когда условие истинно, а следствие ложно Пример: Если выучишь
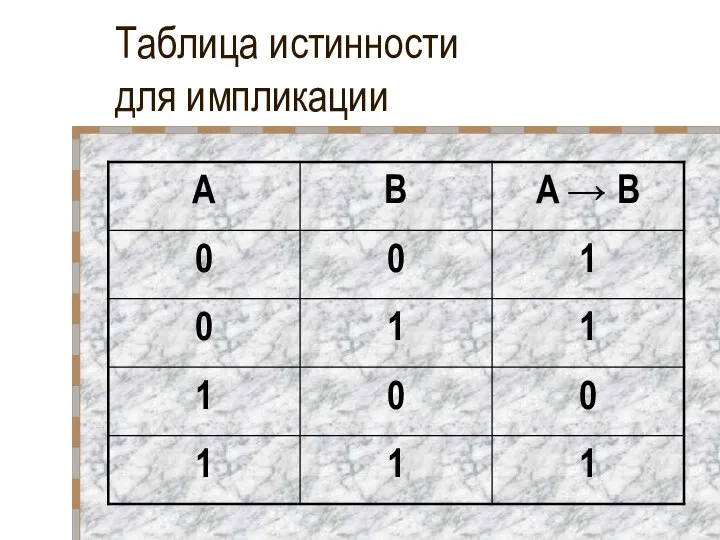
- 31. Таблица истинности для импликации
- 32. Эквивалентность Эквивалентность – это логическая операция, объединяющая два простых высказывания в одно составное и которое является
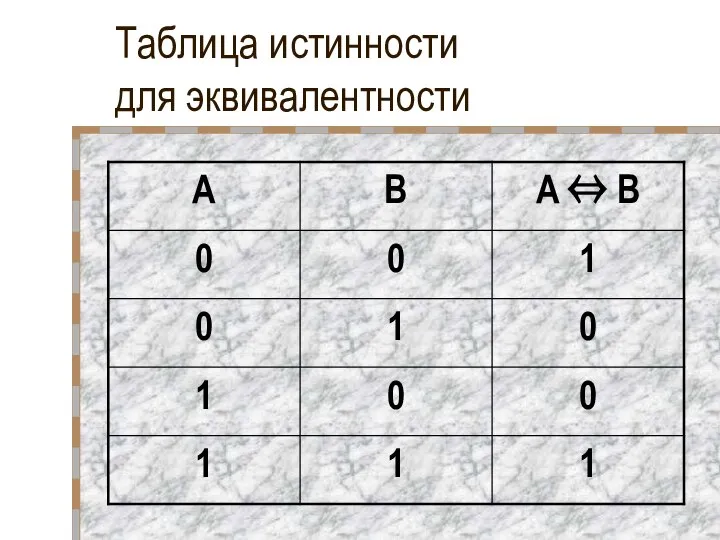
- 33. Таблица истинности для эквивалентности
- 34. Переместительный Дизъюнкция: X ∨ Y ≡ Y ∨ X Конъюнкция: X ∧ Y ≡ Y ∧
- 35. Сочетательный Дизъюнкция: X ∨ (Y ∨ Z) ≡ (X ∨ Y) ∨ Z Конъюнкция: X ∧
- 36. Распределительный Дизъюнкция: X ∧ (Y ∨ Z) ≡ X ∧ Y ∨ X ∧ Z Конъюнкция:
- 37. Правила де Моргана Дизъюнкция: ¬(X ∨ Y) ≡ ¬X ∧ ¬Y Конъюнкция: ¬(X ∧ Y) ≡
- 38. Идемпотенции Дизъюнкция: X ∨ X ≡ X Конъюнкция: X ∧ X ≡ X Основные законы алгебры
- 39. Поглощения Дизъюнкция: X ∨ (X ∧ Y) ≡ X Конъюнкция: X ∧ (X ∨ Y) ≡
- 40. Склеивания Дизъюнкция: (X ∧ Y) ∨ (¬X ∧ Y) ≡ Y Конъюнкция: (X ∨ Y) ∧
- 41. Переменная со своей инверсией Дизъюнкция: X ∨ ¬X ≡ 1 Конъюнкция: X ∧ ¬X ≡ 0
- 42. Операция с константами Дизъюнкция: X ∨ 0 ≡ X, X ∨ 1 ≡ 1 Конъюнкция: X
- 43. Двойного отрицания ¬(¬X) ≡ X Основные законы алгебры высказываний
- 45. Скачать презентацию


















![Логическое отрицание (инверсия) делает истинное высказывание ложным, а ложное – истинным [логическая отрицательная единица, перевертыш]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1291728/slide-22.jpg)

















 Бальмонт Константин Дмитриевич (1867—1942)
Бальмонт Константин Дмитриевич (1867—1942) ВКР: Совершенствование системы управления персоналом
ВКР: Совершенствование системы управления персоналом Успенский Трифонов монастырь
Успенский Трифонов монастырь Работа на средствах связи. Выполнение нормативов и учебных задач
Работа на средствах связи. Выполнение нормативов и учебных задач Противодействие современным преследованиям христиан на Ближнем Востоке
Противодействие современным преследованиям христиан на Ближнем Востоке Презентация Оценка Результативности экономической деятельности таможенных органов
Презентация Оценка Результативности экономической деятельности таможенных органов Банная станция
Банная станция Совершенствование методического обеспечения оценки эффективности деятельности таможенных органов
Совершенствование методического обеспечения оценки эффективности деятельности таможенных органов Презентация Концепция широкомасштабного освоения в таможенных органах международных стандартов ИСО серии 9000 «Системы менеджмен
Презентация Концепция широкомасштабного освоения в таможенных органах международных стандартов ИСО серии 9000 «Системы менеджмен Россия
Россия  Программно-целевое планирование. Новый государственный менеджмент
Программно-целевое планирование. Новый государственный менеджмент Aircompany rules
Aircompany rules Особенности договора поставки товаров: структуру, содержание, правовое регулирование Выполнили: Карпенко Николай Маштанов Миха
Особенности договора поставки товаров: структуру, содержание, правовое регулирование Выполнили: Карпенко Николай Маштанов Миха «Вредные советы Оратору». Юмористически-познавательная работа для всех кто выступает с презентациями
«Вредные советы Оратору». Юмористически-познавательная работа для всех кто выступает с презентациями Введение в SAP NetWeaver
Введение в SAP NetWeaver Совет по внешней и оборонной политике
Совет по внешней и оборонной политике Wir lernen lesen - презентация для начальной школы
Wir lernen lesen - презентация для начальной школы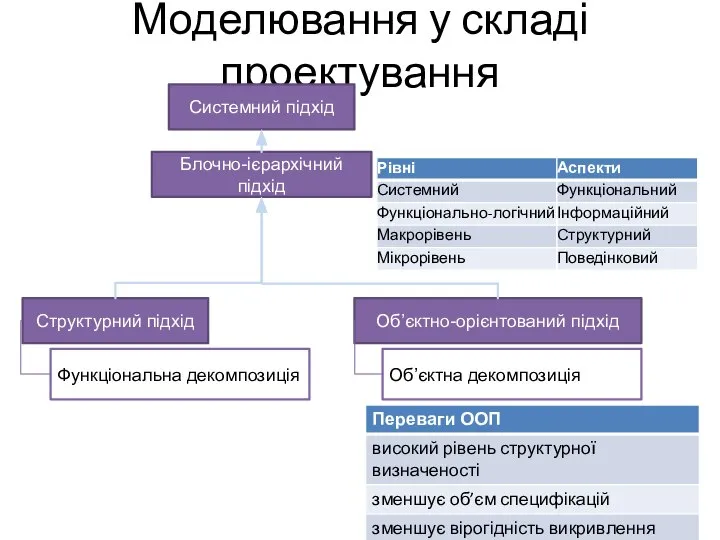 Моделювання у складі проектування
Моделювання у складі проектування Определение Пневмония (воспаление легких) - инфекционное поражение альвеол,сопровождающееся инфильтрацией паренхимы воспали
Определение Пневмония (воспаление легких) - инфекционное поражение альвеол,сопровождающееся инфильтрацией паренхимы воспали Приморье за спорт. Проект
Приморье за спорт. Проект Презентация "Василий Иванович Суриков. «Взятие снежного городка» 1891 г, ГРм, СПб" - скачать презентации по МХК
Презентация "Василий Иванович Суриков. «Взятие снежного городка» 1891 г, ГРм, СПб" - скачать презентации по МХК Система разработки программ для промышленных контроллеров CONT-Designer
Система разработки программ для промышленных контроллеров CONT-Designer Екіпірування гравців у футбол. Правило 4
Екіпірування гравців у футбол. Правило 4 Прикладные методы решения задач строительной механики
Прикладные методы решения задач строительной механики Проведение PR-кампаний
Проведение PR-кампаний Здоровый образ жизни
Здоровый образ жизни Иерархическая структура данных и рациональная тарелка питания
Иерархическая структура данных и рациональная тарелка питания Лыжная подготовка в школе
Лыжная подготовка в школе