Содержание
- 2. Преобразования координат . Если при всех i = 1, 2, …, N функции fi – линейные
- 3. Метод однородных координат . V=(x, y, z, w) [ X Y Z 1 ] = [
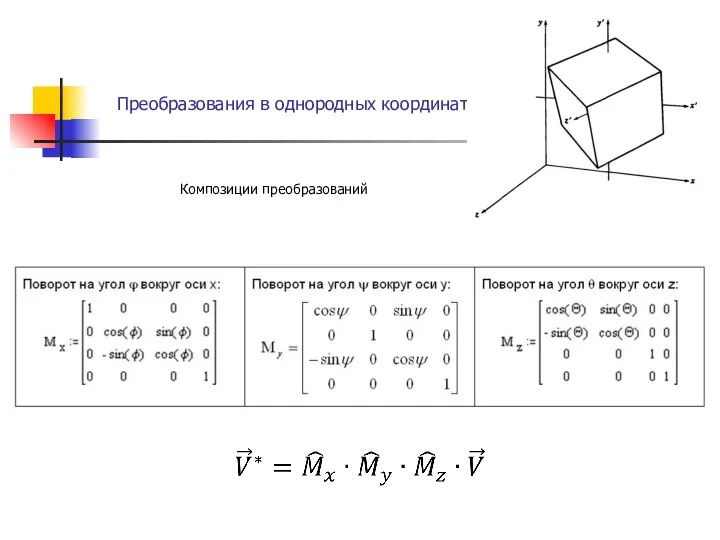
- 4. Преобразования в однородных координатах . Композиции преобразований
- 5. Преобразования Эйлера . Любое заданное направление осей объектной системы координат можно получить, выполняя три поворота вокруг
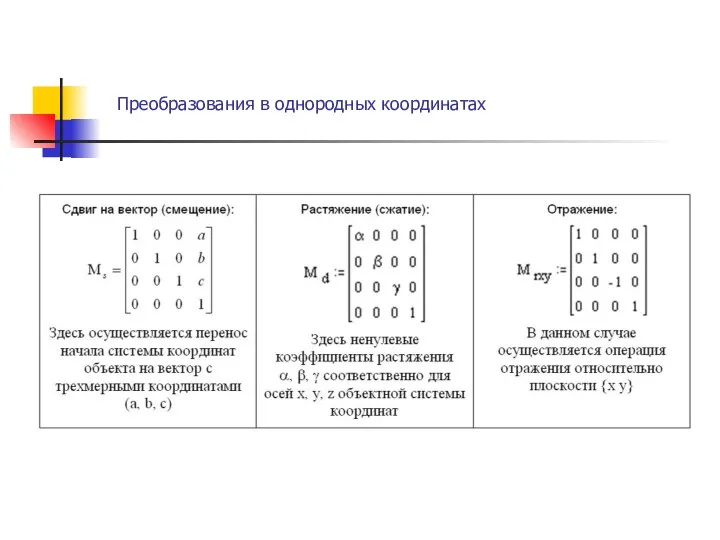
- 6. Преобразования в однородных координатах .
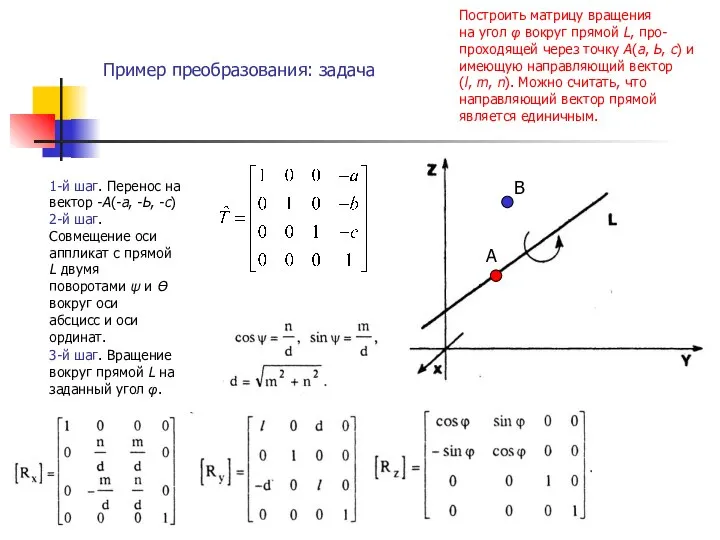
- 7. Пример преобразования: задача . 1-й шаг. Перенос на вектор -А(-а, -Ь, -с) Построить матрицу вращения на
- 8. Пример преобразования (продолжение) . 4-й шаг. Поворот вокруг оси ординат на угол -Ө. 5-й шаг. Поворот
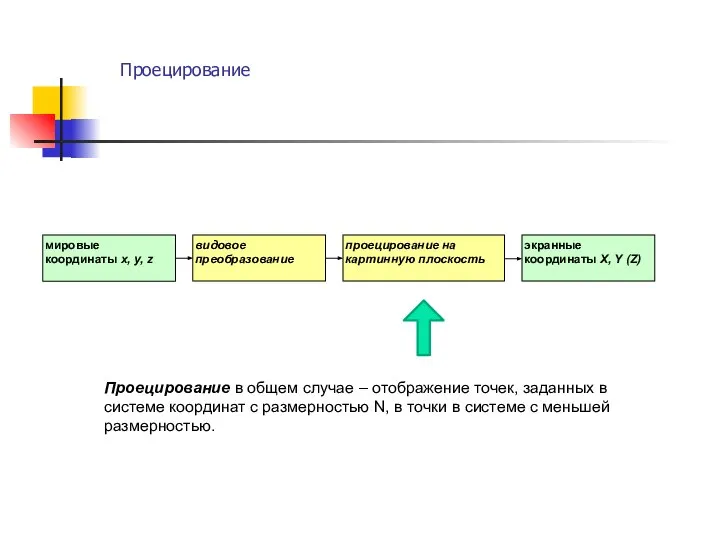
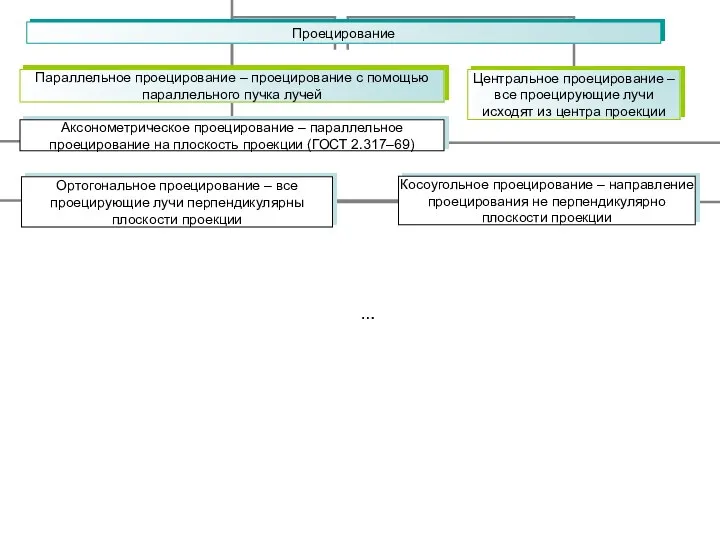
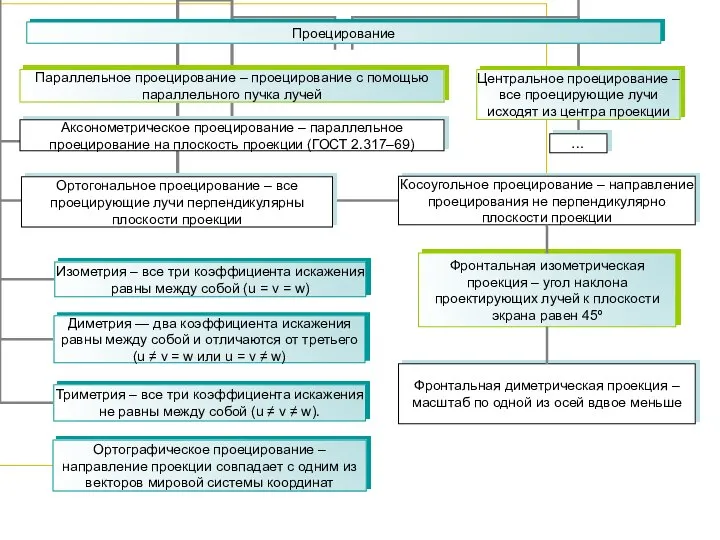
- 9. Проецирование . Проецирование в общем случае – отображение точек, заданных в системе координат с размерностью N,
- 10. Проецирование . …
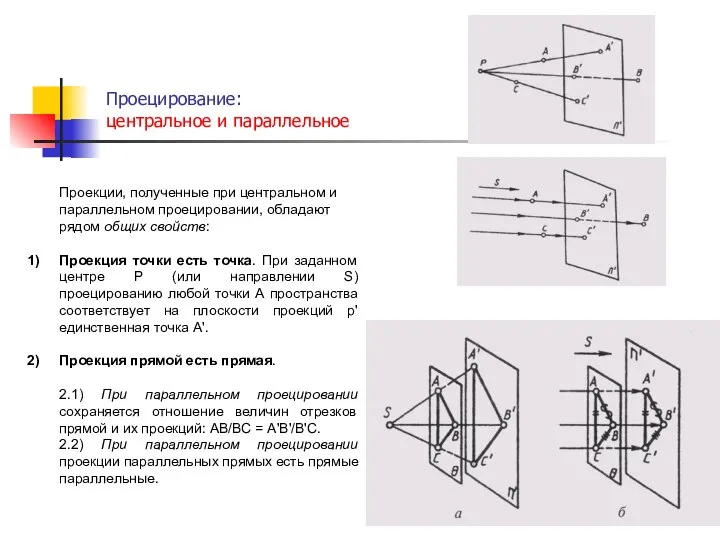
- 11. Проецирование: центральное и параллельное . Проекции, полученные при центральном и параллельном проецировании, обладают рядом общих свойств:
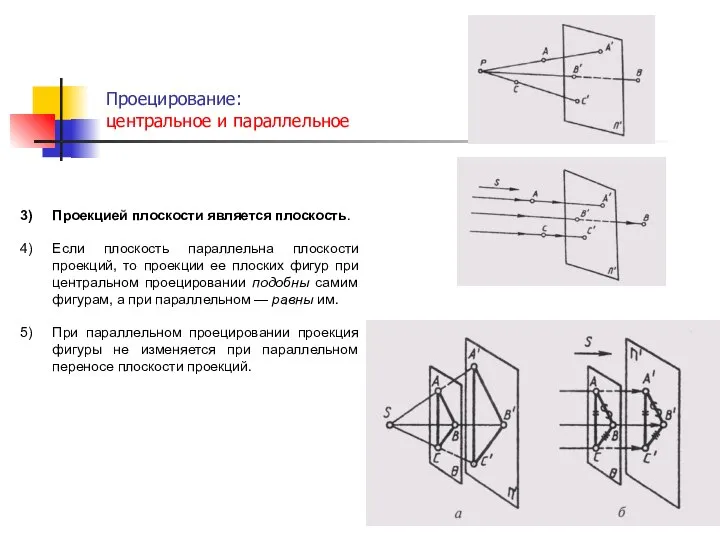
- 12. Проецирование: центральное и параллельное . Проекцией плоскости является плоскость. Если плоскость параллельна плоскости проекций, то проекции
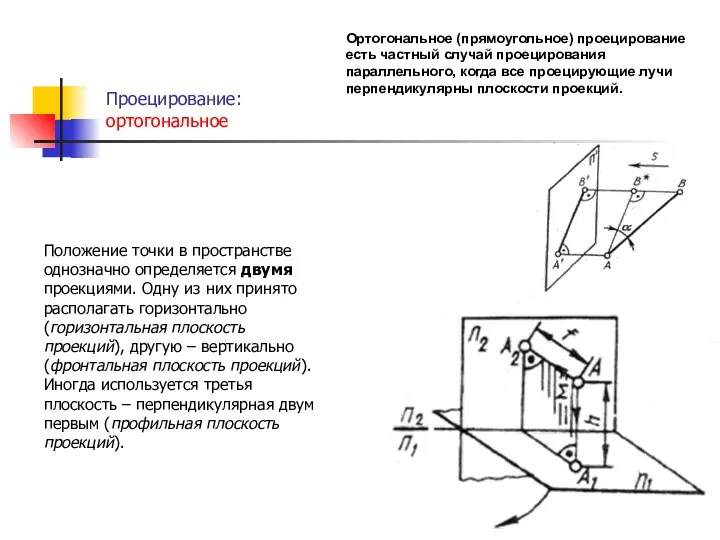
- 13. Проецирование: ортогональное . Положение точки в пространстве однозначно определяется двумя проекциями. Одну из них принято располагать
- 14. Проецирование: аксонометрическое . Аксонометрические проекции в зависимости от направления проецирования разделяют на: косоугольные, когда направление проецирования
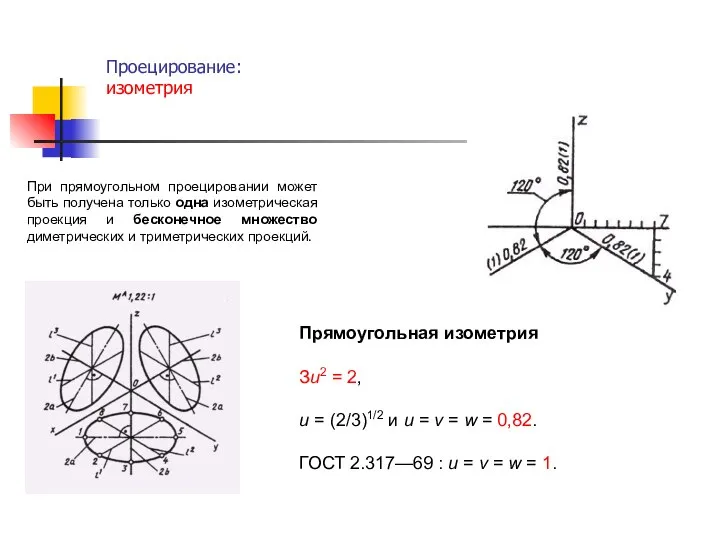
- 16. Проецирование: изометрия . При прямоугольном проецировании может быть получена только одна изометрическая проекция и бесконечное множество
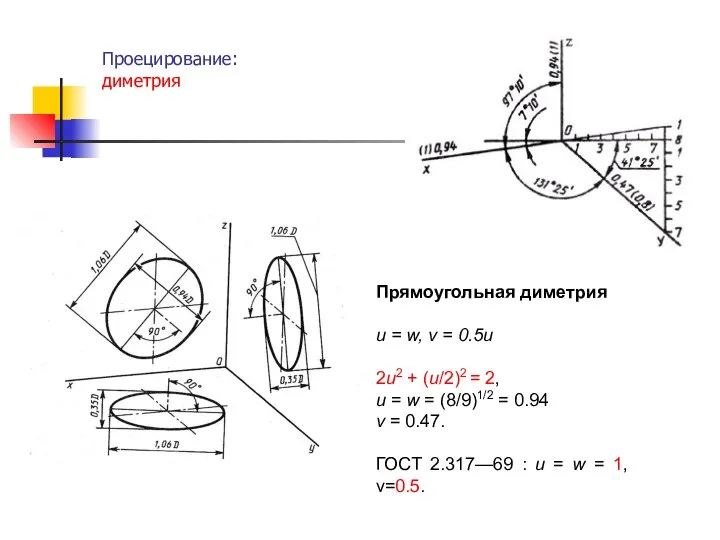
- 17. Проецирование: диметрия . Прямоугольная диметрия u = w, v = 0.5u 2u2 + (u/2)2 = 2,
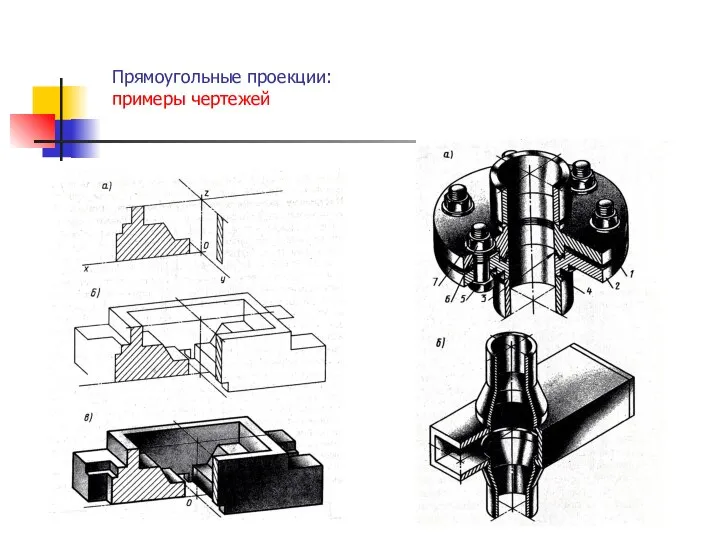
- 18. Прямоугольные проекции: примеры чертежей .
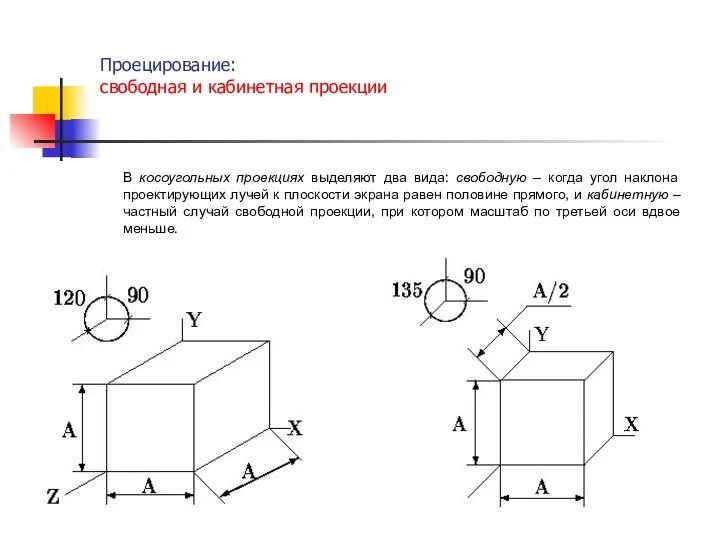
- 19. Проецирование: свободная и кабинетная проекции . В косоугольных проекциях выделяют два вида: свободную – когда угол
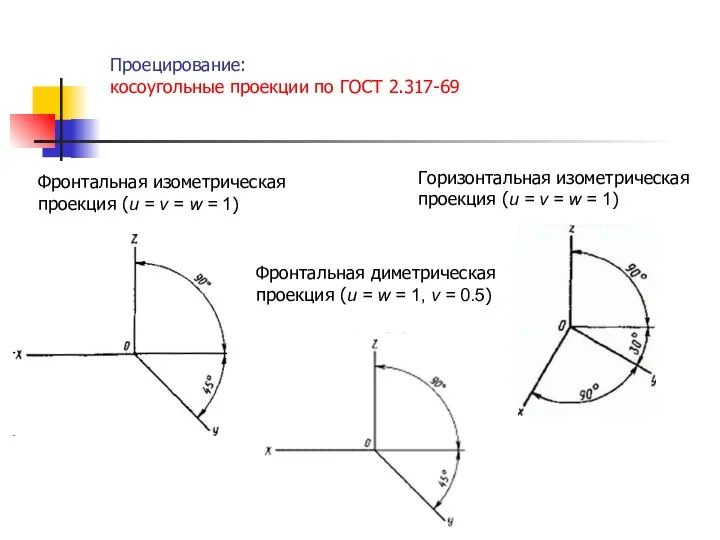
- 20. Проецирование: косоугольные проекции по ГОСТ 2.317-69 Фронтальная изометрическая проекция (u = v = w = 1)
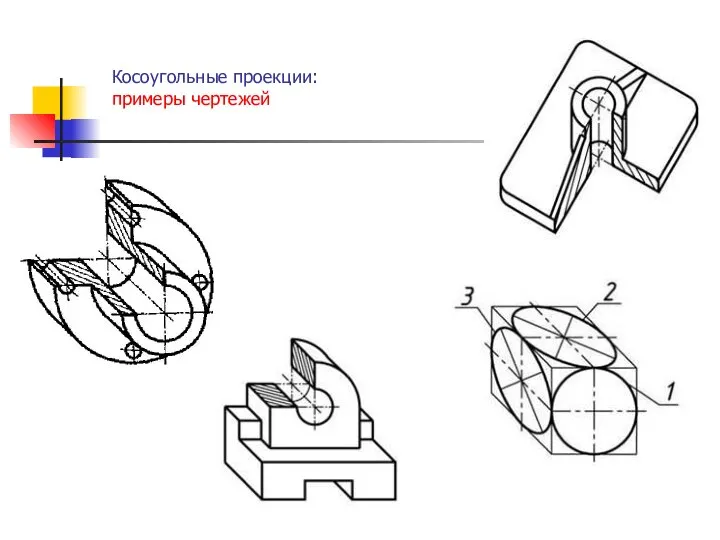
- 21. Косоугольные проекции: примеры чертежей
- 22. Проецирование в однородных координатах . Косоугольное проецирование Ортографическое проецирование вдоль Z на плоскость XY Общий случай
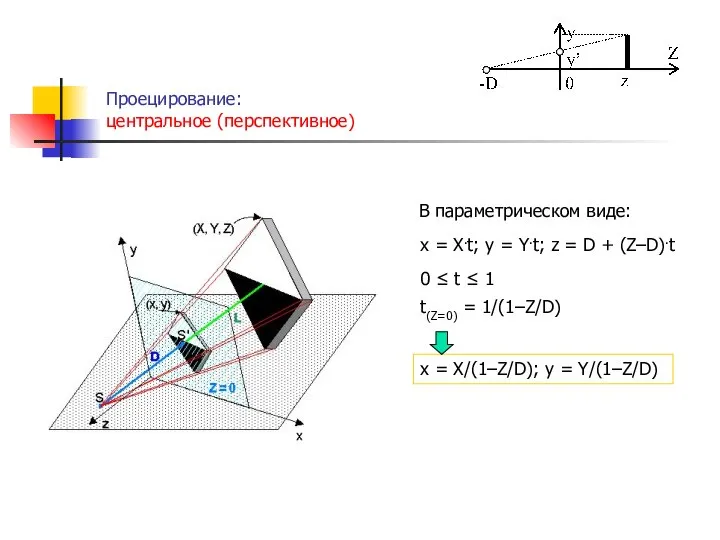
- 23. Проецирование: центральное (перспективное) . x = X.t; y = Y.t; z = D + (Z–D).t 0
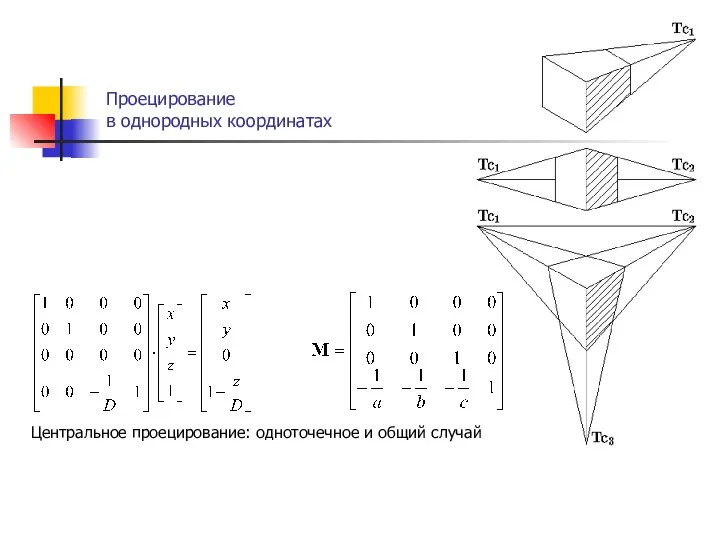
- 24. Проецирование в однородных координатах . Центральное проецирование: одноточечное и общий случай
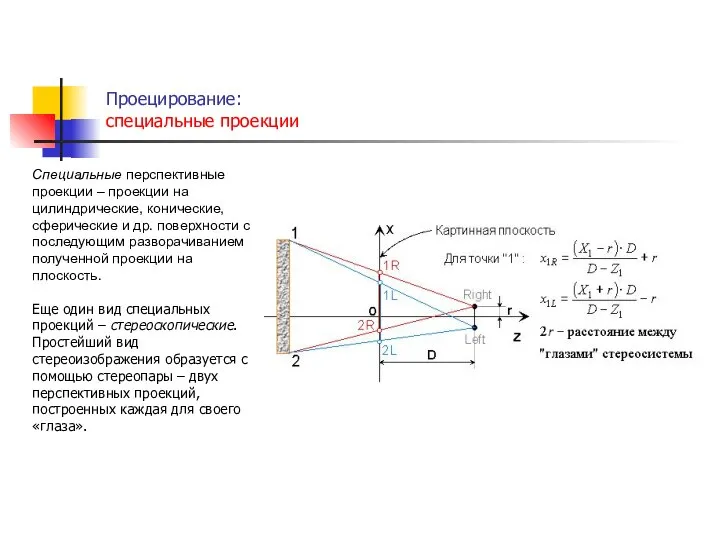
- 25. Проецирование: специальные проекции . Специальные перспективные проекции – проекции на цилиндрические, конические, сферические и др. поверхности
- 26. Проецирование: пример стереоизображения .
- 27. Проецирование: стереограмма .
- 29. Скачать презентацию








 Три фактора распространения болезней
Три фактора распространения болезней  МКОУ «Кулунская оош» Акция « Я выбираю спорт как альтернативу пагубным привычкам»
МКОУ «Кулунская оош» Акция « Я выбираю спорт как альтернативу пагубным привычкам»  Разминка по экологическому праву. Подготовила студентку 2 курса юридического факультета группы Ю124Б Тужилова Л.В.
Разминка по экологическому праву. Подготовила студентку 2 курса юридического факультета группы Ю124Б Тужилова Л.В. Технология обучения в сотрудничестве на уроке английского языка (ТОСУА) Основная идея ТОСУА – создание условий для активной учеб
Технология обучения в сотрудничестве на уроке английского языка (ТОСУА) Основная идея ТОСУА – создание условий для активной учеб «Проектная деятельность учащихся» Семинар учителей МОУ СОШ № 27 пгт Смоляниново
«Проектная деятельность учащихся» Семинар учителей МОУ СОШ № 27 пгт Смоляниново Презентация "Стили и направления изобразительного искусства. ХХ век" - скачать презентации по МХК
Презентация "Стили и направления изобразительного искусства. ХХ век" - скачать презентации по МХК Строительство универсальной спортивной площадки на территории микрорайона «Южный-2» в с. Завьялово
Строительство универсальной спортивной площадки на территории микрорайона «Южный-2» в с. Завьялово Презентация на тему "Профессиональная компетентность учителя" - скачать презентации по Педагогике
Презентация на тему "Профессиональная компетентность учителя" - скачать презентации по Педагогике Қайта даму дəуірінің костюмі
Қайта даму дəуірінің костюмі армения старшая группа
армения старшая группа Презентация«Аудит документов по оформлению импортных операций»
Презентация«Аудит документов по оформлению импортных операций»  Табличка на стол (только для CI Дилеров)
Табличка на стол (только для CI Дилеров) Эволюция ЕСТЕСТВЕННОНАУЧНОЙ КАРТИНЫ МИРА. Подготовили: Кондратьев Александр Акинбани Виктория
Эволюция ЕСТЕСТВЕННОНАУЧНОЙ КАРТИНЫ МИРА. Подготовили: Кондратьев Александр Акинбани Виктория Инструкция по использованию инфомата для записи к врачу в порядке электронной очереди с помощью портала пациента
Инструкция по использованию инфомата для записи к врачу в порядке электронной очереди с помощью портала пациента Полевые транзисторы. Основные сведения и классификация
Полевые транзисторы. Основные сведения и классификация Ватутин Николай Фёдорович
Ватутин Николай Фёдорович Архитектурная климатология
Архитектурная климатология Serial Communications
Serial Communications Техническая диагностика подвижного состава
Техническая диагностика подвижного состава Тема : «Классный руководитель – архитектор классного коллектива»
Тема : «Классный руководитель – архитектор классного коллектива» Растревоженная душа В. Шукшина. К 90 – летию писателя
Растревоженная душа В. Шукшина. К 90 – летию писателя 29 ноября - День матери
29 ноября - День матери Презентация ЖК “Лефортово Парк”
Презентация ЖК “Лефортово Парк” Презентация Безопасность продовольственных и непродовольственных товаров
Презентация Безопасность продовольственных и непродовольственных товаров В мире головоломок - презентация для начальной школы_
В мире головоломок - презентация для начальной школы_ Общественный строй в виде тест-тренинга
Общественный строй в виде тест-тренинга Презентация Режим пограничной зоны, территориальных и внутренних вод
Презентация Режим пограничной зоны, территориальных и внутренних вод Степень с целым показателем. 8 класс 1.04.13
Степень с целым показателем. 8 класс 1.04.13