Содержание
- 2. 3.1 Абстрактный граф Граф можно определить как совокупность двух множеств: G = (V, E), где V
- 3. Само понятие графа подразумевает графическое представление данного объекта. Вершины изображаются точками, а ребра – линиями, соединяющими
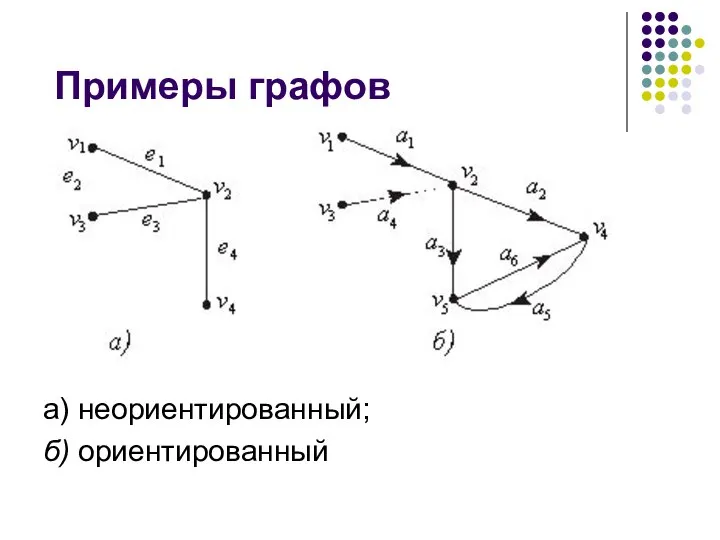
- 4. Примеры графов а) неориентированный; б) ориентированный
- 5. Вершины неориентированного графа, связываемые ребром, считаются концами этого ребра. Принято обозначать ребра также парами их концов,
- 6. Между вершинами и ребрами неориентированного графа так же, как между вершинами и дугами ориентированного графа, существует
- 7. Граф может содержать петли, т. е. ребра, концы которых совпадают, или дуги, у которых начало совпадает
- 8. В ориентированном графе с некоторой вершиной v подобным образом связаны два множества: полуокрестность исхода N +(v)
- 9. Можно говорить об окрестности N(v) и степени d(v) вершины v ориентированного графа. При этом Для неориентированного
- 10. Для ориентированного графа с множеством дуг А имеем В практических приложениях граф (ориентированный или неориентированный), как
- 11. Граф G = (V, E), у которого множество ребер пусто, т. е. Е = ∅, называется
- 12. Граф называется двудольным, если множество его вершин V разбито на два непересекающихся подмножества V′ и V′′
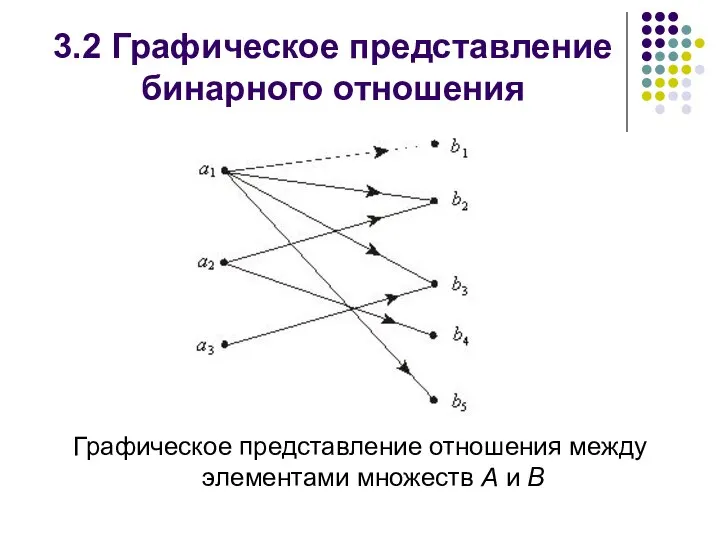
- 13. 3.2 Графическое представление бинарного отношения Графическое представление отношения между элементами множеств А и В
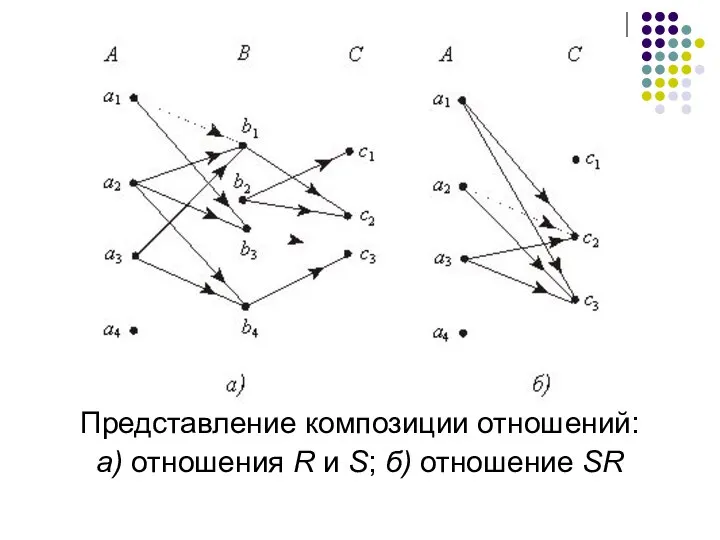
- 14. Представление композиции отношений: а) отношения R и S; б) отношение SR
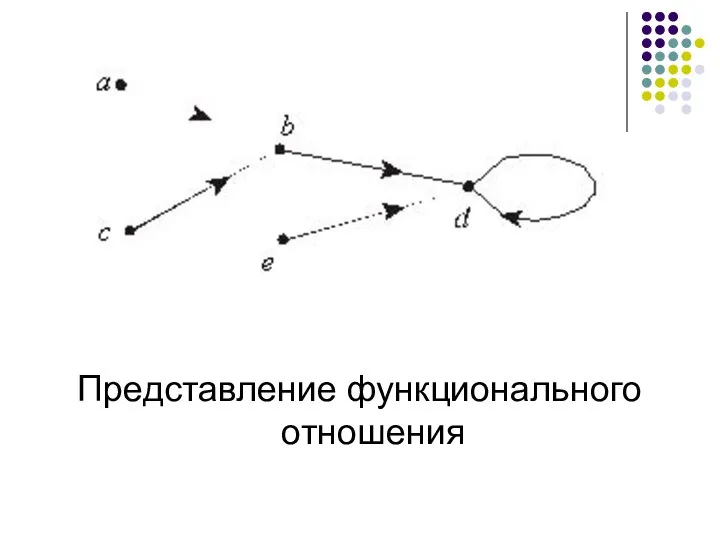
- 15. Представление функционального отношения
- 16. 3.3 Матричные представления графа Поскольку граф можно рассматривать как графическое представление некоторого бинарного отношения, его можно
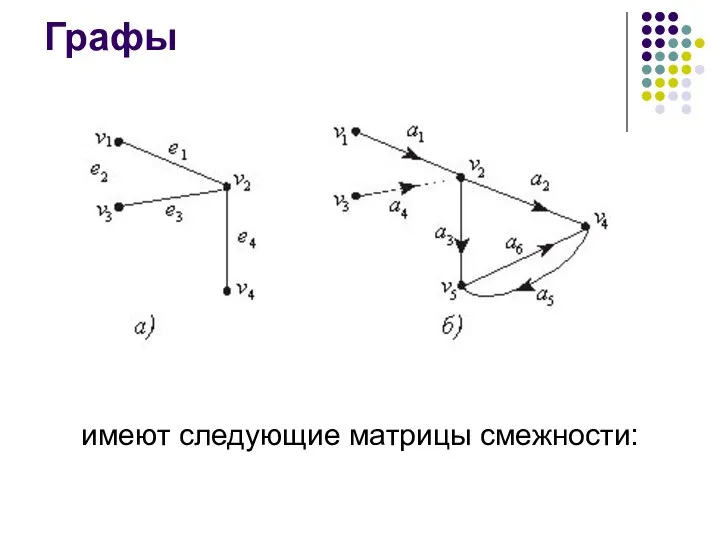
- 17. Графы имеют следующие матрицы смежности:
- 18. Нетрудно видеть, что матрица смежности неориентированного графа обладает симметрией относительно главной диагонали.
- 19. Ориентированный граф можно задать также матрицей инцидентности, которая определяется следующим образом. Ее строки соответствуют вершинам графа,
- 20. Матрицы инцидентности этиз графов будут иметь следующий вид:
- 21. Заметим, что при матричном представ- лении графа его вершины, а также реб- ра или дуги оказываются
- 22. 3.4 Части графа Граф Н = (W, F) называется подграфом графа G = (V, E), если
- 23. Любая последовательность вида v1, e1, v2, e2, … , ek, vk+1, где v1, v2, … ,
- 24. Маршрут, все ребра которого различны, называется цепью. Цепь, все вершины которой различны, называется простой цепью. С
- 25. 3.5 Достижимость и связность Граф является связным, если между любыми двумя его вершинами имеется цепь. Связный
- 26. В ориентированном графе маршрутом называется последовательность вида v1, а1, v2, а2, … , аk, vk+1, где
- 27. Вершина vj в ориентированном графе является достижимой из вершины vj, если в этом графе имеется путь
- 28. Очевидно, что все диагональные элементы матрицы R равны 1 (xj достижима из xi). Пусть через Г(xi)
- 29. Алгоритм Кристофидеса. Множество R(xi) получается последова-тельным выполнением (слева направо) операций объединения в соотношении () до тех
- 30. Пусть через Г-1(xi) обозначено множество вершин, из которых можно достичь вершину xi. С использованием путей длины
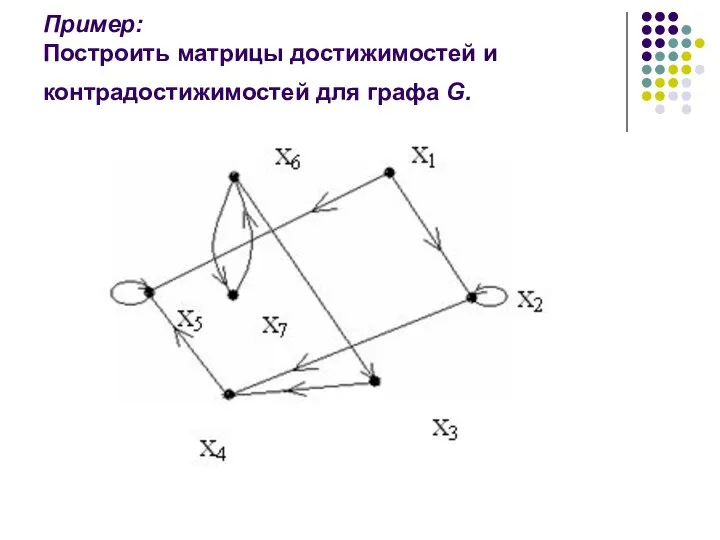
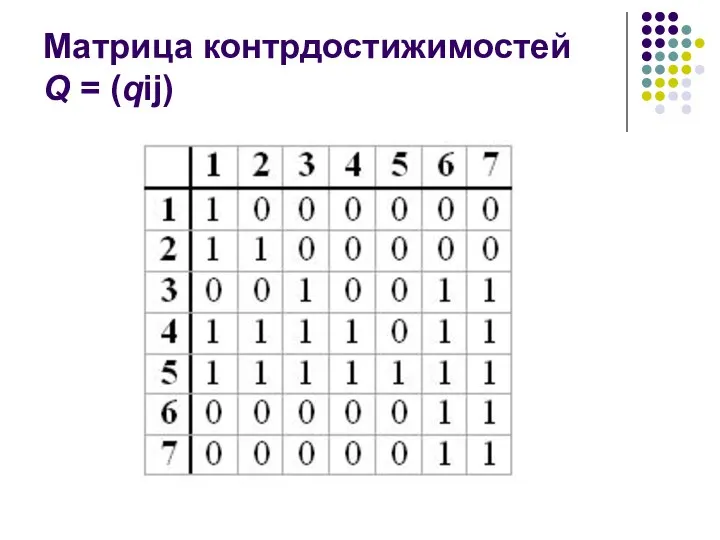
- 31. Пример: Построить матрицы достижимостей и контрадостижимостей для графа G.
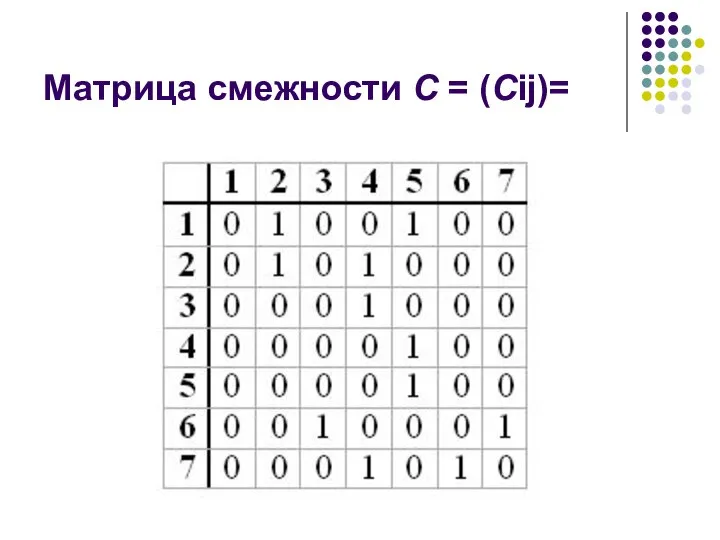
- 32. Матрица смежности C = (Cij)=
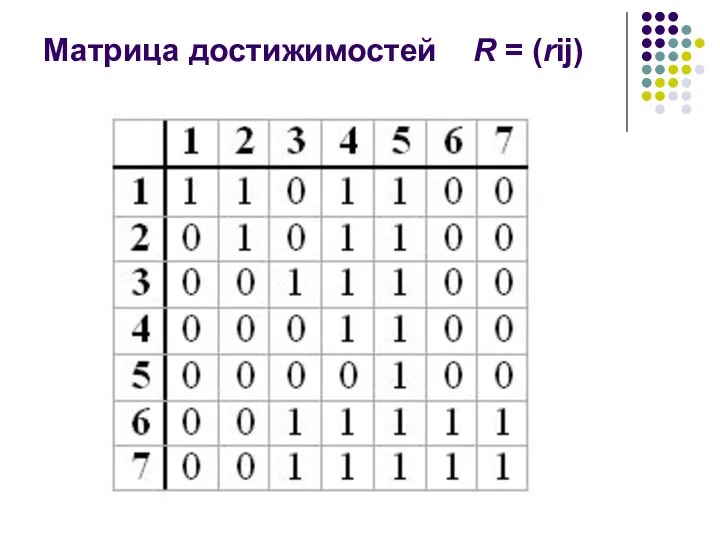
- 33. Матрица достижимостей R = (rij)
- 34. Матрица контрдостижимостей Q = (qij)
- 35. 3.6 Доминирующие множества графа Подмножество S множества вершин V графа G называется доминирующим множеством графа G,
- 36. Если S является доминирующим множест- вом некоторого графа G, то всякое множес- тво вершин S′ ⊇
- 37. Наглядным примером задачи о наимень- шем доминирующем множестве является одна из задач о ферзях, где надо
- 38. Задача о наименьшем доминирующем множестве сводится к известной задаче о кратчайшем покрытии, которая подроб- но будет
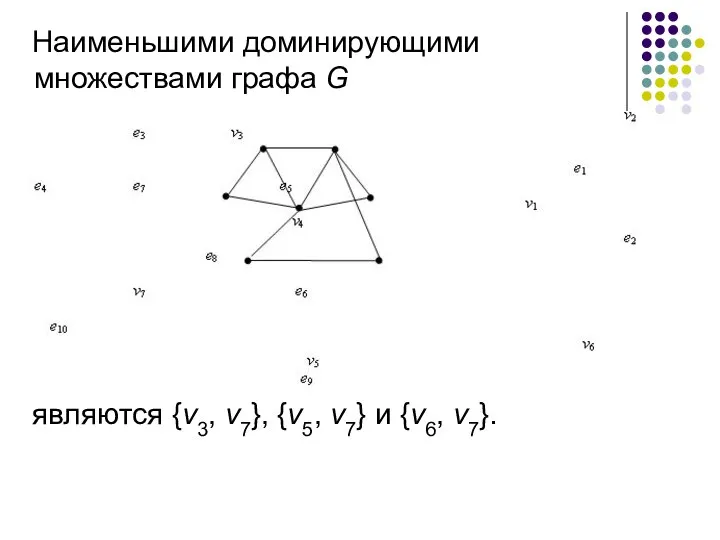
- 39. Наименьшими доминирующими множествами графа G являются {v3, v7}, {v5, v7} и {v6, v7}.
- 40. Его матрица смежности, дополненная единицами на главной диагонали, имеет вид Каждое из соответствующих множеств строк рассматриваемой
- 41. 3.7 Независимые множества графа Подмножество S множества вершин V графа G называется независимым множеством графа G,
- 42. Независимое множество, имеющее наибольшую мощность среди всех независимых множеств графа G, называют наибольшим независимым множеством, а
- 43. 3.8 Раскраска графа Раскраской некоторого графа G = (V, Е) называется такое разбиение множества вершин V
- 44. Иногда ставится задача раскраски ребер графа G = (V, Е), где требуется получить такое разбиение множества
- 45. Иногда можно получить раскраску графа, минимальную или близкую к минималь- ной, с помощью так называемого «жадного»
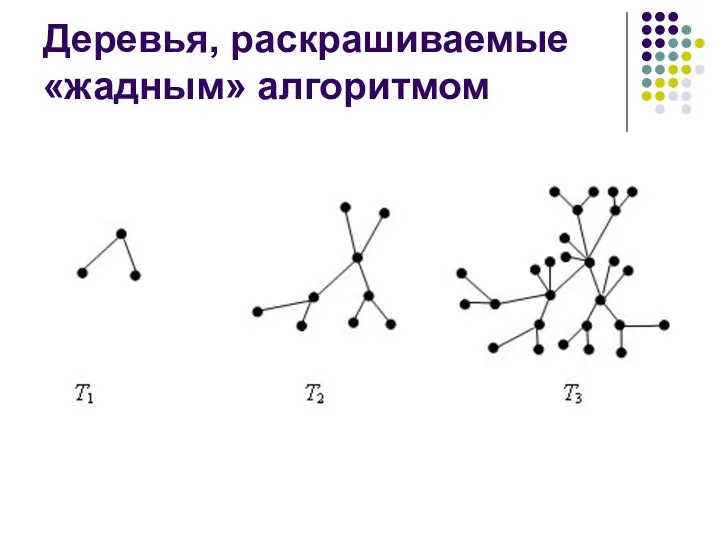
- 46. Рассмотрим неограниченную последовательность деревьев Т1, Т2, … , Тi. Дерево Т1 состоит из трех вершин и
- 47. Деревья, раскрашиваемые «жадным» алгоритмом
- 48. Бихроматические графы Граф G называется k-хроматическим, если γ(G) = k. Очевидно, пустые и только пустые графы
- 49. Т е о р е м а К ё н и г а Непустой граф является
- 50. 3.9 Планарность графов Количество граней можно найти для плоского связного графа. Плоский граф – граф, который
- 52. Скачать презентацию






































 Оценка эффективности обучения: как показать ценность руководству и сотрудникам компании «Амплуа-Брокер», ©, 2009
Оценка эффективности обучения: как показать ценность руководству и сотрудникам компании «Амплуа-Брокер», ©, 2009 Грамматический строй ОЕ периода
Грамматический строй ОЕ периода Опыт борьбы с коррупцией в Сингапуре Подготовила Студентка ФТД-4 группы Т-094 Шевченко Наталья
Опыт борьбы с коррупцией в Сингапуре Подготовила Студентка ФТД-4 группы Т-094 Шевченко Наталья Дәстүр, әдет-ғұрып ырымдардың тәрбиелік маңызы
Дәстүр, әдет-ғұрып ырымдардың тәрбиелік маңызы Презентация ЭКСПЕРТИЗА МЯСНЫХ КОНСЕРВОВ
Презентация ЭКСПЕРТИЗА МЯСНЫХ КОНСЕРВОВ Новое о светофоре 1. О светофорах 2. Игра «Сигналы светофора»
Новое о светофоре 1. О светофорах 2. Игра «Сигналы светофора» «Содержание современных педагогических технологий на уроке английского языка. Особенности проектных технологий» Учител
«Содержание современных педагогических технологий на уроке английского языка. Особенности проектных технологий» Учител Организационное поведение © Бараусова Елена Александровна
Организационное поведение © Бараусова Елена Александровна ПП тема 1
ПП тема 1 Финансовая отчетность банка ВТБ Петрова Маргарита Куркина анна 3 курс фм
Финансовая отчетность банка ВТБ Петрова Маргарита Куркина анна 3 курс фм Народный праздничный костюм
Народный праздничный костюм Создание игровой куклы
Создание игровой куклы Культура России в 10 - 13 веке
Культура России в 10 - 13 веке ТЕМА № 3. Природные предпосылки социально-экономического развития России
ТЕМА № 3. Природные предпосылки социально-экономического развития России ГОУ ВПО Нижегородская государственная медицинская академия «Медицинские сестры - организаторы терапевтического обучения пац
ГОУ ВПО Нижегородская государственная медицинская академия «Медицинские сестры - организаторы терапевтического обучения пац Методы физического воспитания. Лекция
Методы физического воспитания. Лекция Понятие и виды себестоимости
Понятие и виды себестоимости Тема 2 «Центральный банк РФ»
Тема 2 «Центральный банк РФ»  Дробященко Наталья Юрьевна Член правления коллегии пенсионных актуариев 5 октября 2006 год
Дробященко Наталья Юрьевна Член правления коллегии пенсионных актуариев 5 октября 2006 год  Логические основы ЭВМ
Логические основы ЭВМ Документационное обеспечение управления
Документационное обеспечение управления XX съезд КПСС. Разоблачение культа личности Сталина
XX съезд КПСС. Разоблачение культа личности Сталина  Волны
Волны C++. Функции
C++. Функции 9.1
9.1 Презентация Национальная инновационная система республики Казахстан
Презентация Национальная инновационная система республики Казахстан  Технология ИС
Технология ИС игра
игра