Рассмотрим дифференциальное уравнение первого порядка:
соотношение часто удается записать в виде:
Последнее уравнение
называется дифференциальным уравнением, разрешенным относительно производной. Значение производной равно тангенсу угла наклона касательной к графику функции в точке (x,y). Функцию f(x,y) будем называть правой частью дифференциального уравнения.
Общим решением уравнения будет являться семейство функций y=y(x,c1) различающихся значение постоянной c1. Задаем одно начальное условие y(x0)=y0, которое определяет значение c1и конкретное частное решение – задача Коши.
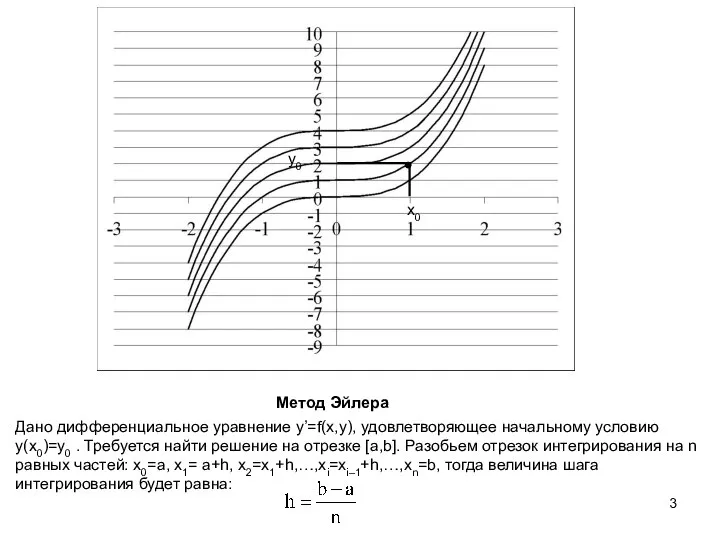
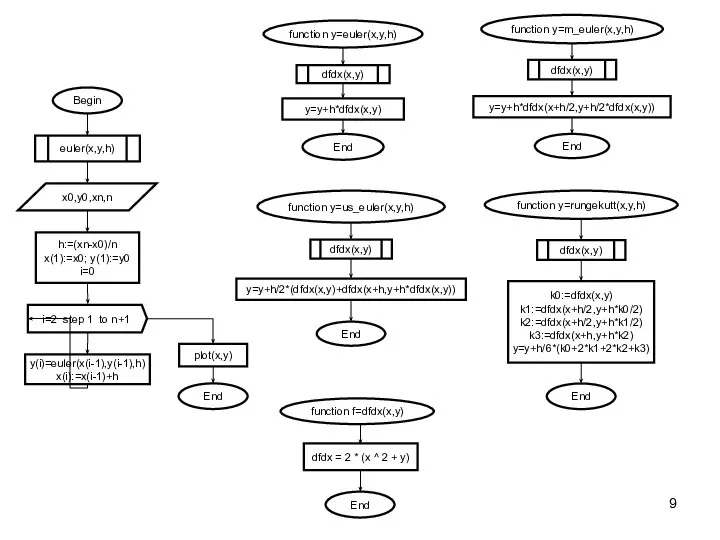
Для простейшего дифференциального уравнения y’=3x2. Общее решение имеет вид y=x3+c, а подставив в общее решение начальное условие x0=1, y0=2 вычислим с=1 и определим частное решение как: y=x3+1




 Архитектура процессоров Intel и AMD
Архитектура процессоров Intel и AMD Нарушения углеводного обмена
Нарушения углеводного обмена Особливості складання основних видів службової документації
Особливості складання основних видів службової документації Геометрические параметры деталей. Основные понятия
Геометрические параметры деталей. Основные понятия Выполнила: Блинова Ксения ученица 8Бкласса Научный руководитель: Васильева Татьяна Николаевна
Выполнила: Блинова Ксения ученица 8Бкласса Научный руководитель: Васильева Татьяна Николаевна Контрактная система Тульской области
Контрактная система Тульской области ГУЗ «Пермский краевой онкологический диспансер» ГОУ ВПО «Пермская государственная медицинская академия им. академика Е.А. Вагне
ГУЗ «Пермский краевой онкологический диспансер» ГОУ ВПО «Пермская государственная медицинская академия им. академика Е.А. Вагне Разработала: преподаватель высшей категории Зеленкина Т.М.
Разработала: преподаватель высшей категории Зеленкина Т.М. Обязанности должностных лиц медицинской службы соединения по медицинскому снабжению
Обязанности должностных лиц медицинской службы соединения по медицинскому снабжению На Дне Презентацию от имени ученика выполнили Кулемина Д. и Романова А. ГОУ ВПО «Поволжская государственная социально-гуманитарн
На Дне Презентацию от имени ученика выполнили Кулемина Д. и Романова А. ГОУ ВПО «Поволжская государственная социально-гуманитарн Дроби. Зажжение олимпийского огня 7 февраля 2014 года, город Сочи
Дроби. Зажжение олимпийского огня 7 февраля 2014 года, город Сочи Кадастровое деление территории
Кадастровое деление территории Культура Месопотамии
Культура Месопотамии Основные направления в пм
Основные направления в пм Антибиотики
Антибиотики  Презентация на тему "Архитектура барокко"
Презентация на тему "Архитектура барокко" Жан-Батист Мольер (биография)
Жан-Батист Мольер (биография) Święty Łukasz Ewangelista
Święty Łukasz Ewangelista PEST Analysis
PEST Analysis Government of the Russian Federation
Government of the Russian Federation Устройство защитного отключения (УЗО)
Устройство защитного отключения (УЗО) Финансовая политика государства
Финансовая политика государства Помехи в каналах связи
Помехи в каналах связи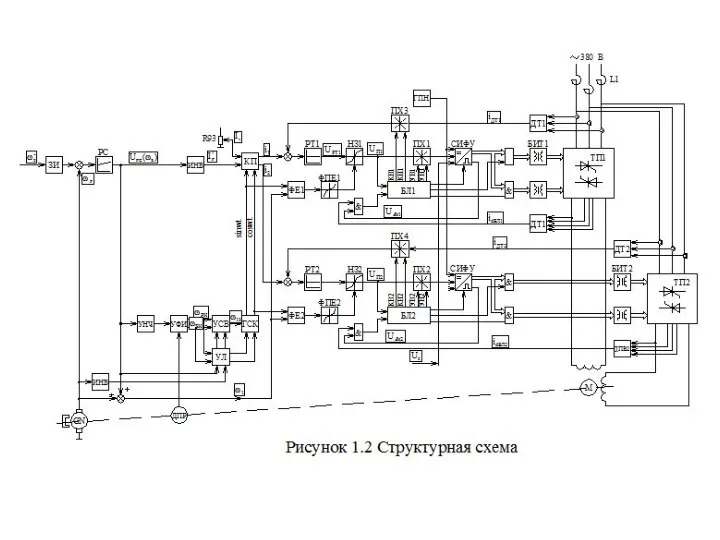 Структурная схема ЭТА1-02
Структурная схема ЭТА1-02 IDU0075 Veebiteenused
IDU0075 Veebiteenused Моя родина Армения
Моя родина Армения АРХИТЕКТУРА Архитектура г. Омска Приложение к хрестоматии «Музыка, театр, изобразительное искусство Омского Прииртышья»
АРХИТЕКТУРА Архитектура г. Омска Приложение к хрестоматии «Музыка, театр, изобразительное искусство Омского Прииртышья» Кратчайшие пути, максимальные потоки и минимальные разрезы на орграфах
Кратчайшие пути, максимальные потоки и минимальные разрезы на орграфах