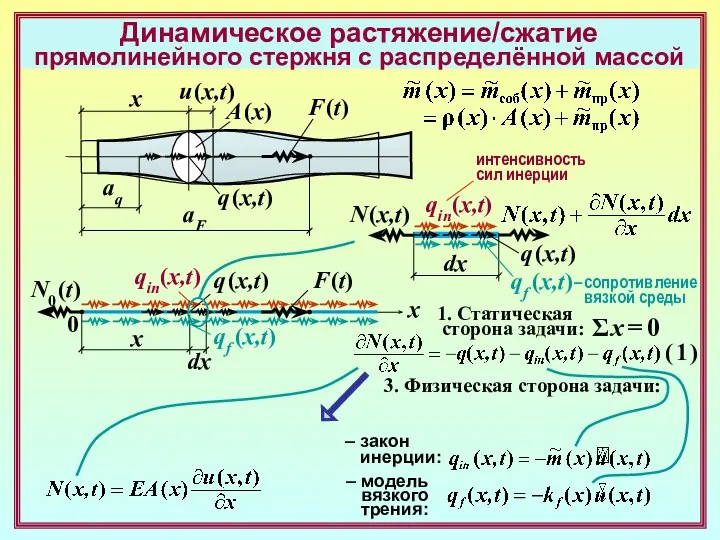
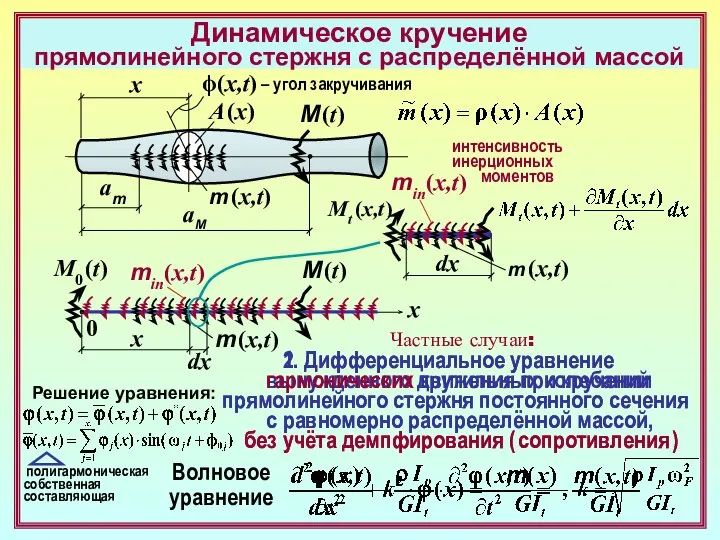
Динамическое растяжение/сжатие прямолинейного стержня с распределённой массой
x
A (x)
q (x,t)
F (t)
u (x,t)
aq
aF
x
x
dx
q
(x,t)
F (t)
qin(x,t)
0
N0 (t)
Частные случаи:
– уравнение в амплитудах перемещений
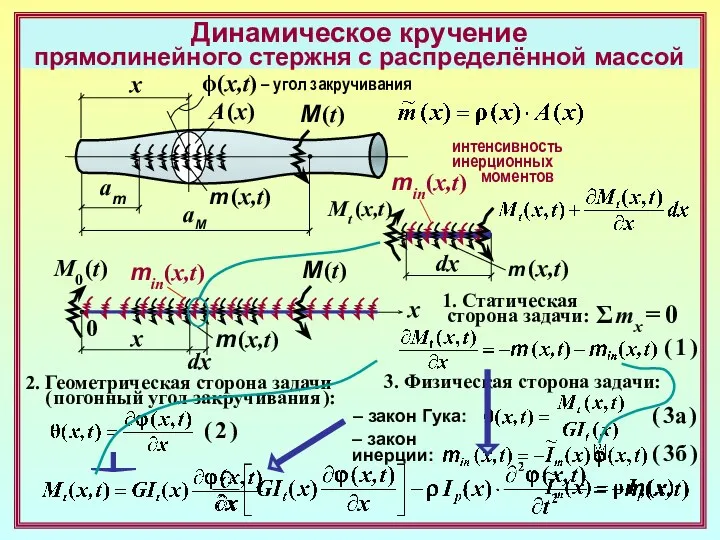
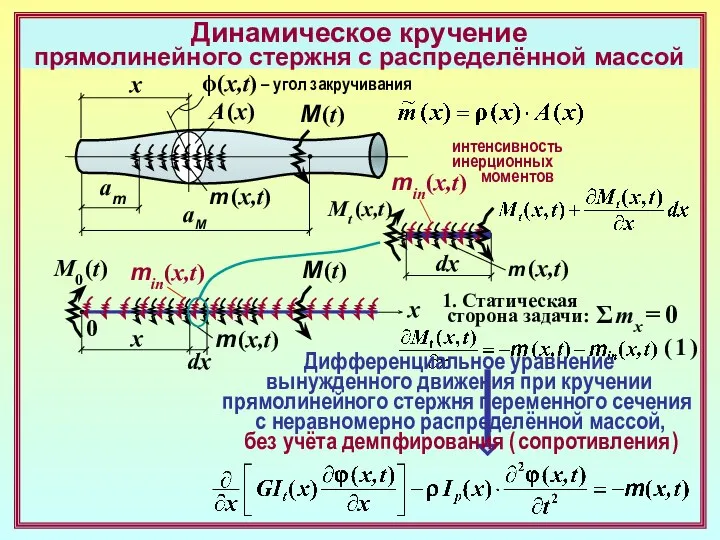
3. Дифференциальное уравнение
гармонического движения
растянутого/сжатого
прямолинейного стержня
постоянного сечения
с равномерно распределённой массой,
без учёта демпфирования ( сопротивления )
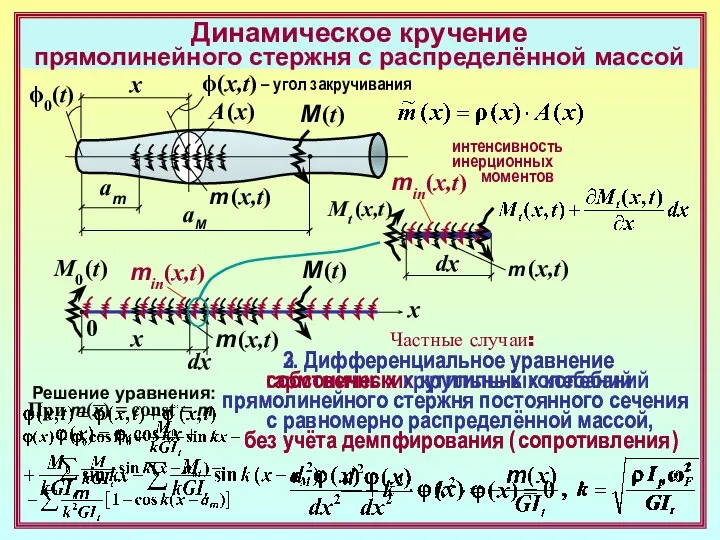
Решение уравнения по МНП при q(x) = const = q :
q (x,t) = q (x)
F (t) = F
qin (x,t) = qin (x)
* sin ωF t
u0(t) = u0
u0(t)
N0(t) = N0
u (x,t) = u (x)
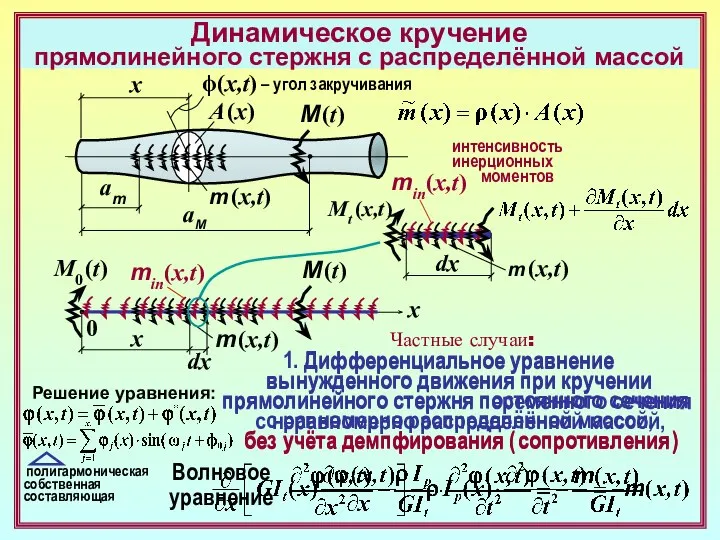
4. Дифференциальное уравнение
собственных колебаний
растянутого/сжатого
прямолинейного стержня
постоянного сечения
с равномерно распределённой массой,
без учёта демпфирования ( сопротивления )
* sin ω t
Решение уравнения по МНП при q(x) = 0 :
F(t) – сила инерции точечной
массы или реакция
упругой продольной связи








 SMARTGOTRENDY_updated (1) (2)
SMARTGOTRENDY_updated (1) (2) Презентация "Ставни и наличники" - скачать презентации по МХК
Презентация "Ставни и наличники" - скачать презентации по МХК Спільне використання ресурсів локальної мережі
Спільне використання ресурсів локальної мережі Антигипертензивные средства (АГС)
Антигипертензивные средства (АГС)  Логически основи в компютъра Изготвил: София Копанарова
Логически основи в компютъра Изготвил: София Копанарова Аттестационная работа. Создание творческого проекта «Традиционные украшения Заонежья»
Аттестационная работа. Создание творческого проекта «Традиционные украшения Заонежья» Япония
Япония Мой дом – моя крепость День Семьи
Мой дом – моя крепость День Семьи Мeine Heimat. 7 Klasse
Мeine Heimat. 7 Klasse Презентация на тему "Ртуть Отравления ртутью Первая медицинская помощь" - скачать презентации по Медицине
Презентация на тему "Ртуть Отравления ртутью Первая медицинская помощь" - скачать презентации по Медицине Современные рыцари
Современные рыцари СИНДРОМ МАЛОГО СЕРДЕЧНОГО ВЫБРОСА: КЛИНИКА, ДИАГНОСТИКА, ЛЕЧЕНИЕ, ПРОФИЛАКТИКА
СИНДРОМ МАЛОГО СЕРДЕЧНОГО ВЫБРОСА: КЛИНИКА, ДИАГНОСТИКА, ЛЕЧЕНИЕ, ПРОФИЛАКТИКА  Фазы напряженного состояния грунта
Фазы напряженного состояния грунта Разъяснения по заполнению заявления-анкеты на получение повышенной стипендии
Разъяснения по заполнению заявления-анкеты на получение повышенной стипендии Влияние на рост школьника занятия тяжелой атлетикой. 8 класс
Влияние на рост школьника занятия тяжелой атлетикой. 8 класс Анализ производства и реализации
Анализ производства и реализации Телевизионные преобразователи. Датчики телевизионных сигналов и их характеристики. Передающие телевизионные трубки. (Лекция 6)
Телевизионные преобразователи. Датчики телевизионных сигналов и их характеристики. Передающие телевизионные трубки. (Лекция 6) Организационная культура
Организационная культура Методы структурированной оценки: SWOT анализ, концептуальная карта, цветовое голосование Вадим Маршаков Екатерина Кузнецова Ю
Методы структурированной оценки: SWOT анализ, концептуальная карта, цветовое голосование Вадим Маршаков Екатерина Кузнецова Ю Робер Дуано – ироничный наблюдатель, лиричный и великий фотограф-гуманист
Робер Дуано – ироничный наблюдатель, лиричный и великий фотограф-гуманист иван грозный
иван грозный Доходы и расходы семьи. Стоимость жизни.
Доходы и расходы семьи. Стоимость жизни.  Диаграмма Парето – определение и назначение
Диаграмма Парето – определение и назначение Управление инновационными процессами в школе
Управление инновационными процессами в школе Духовная культура
Духовная культура РОССИЙСКИЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ КОНЦЕРН «РУСЭЛПРОМ» Объединение предприятий по производству электротехнического оборудования и
РОССИЙСКИЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ КОНЦЕРН «РУСЭЛПРОМ» Объединение предприятий по производству электротехнического оборудования и  Ландшафтное проектирование. Причины и методы реконструкции зеленых насаждений
Ландшафтное проектирование. Причины и методы реконструкции зеленых насаждений Специальность Физическая культура
Специальность Физическая культура