Скорость Волновых пакетов

результат на первый взгляд кажется неожиданным, но ни к каким противоречиям не приводит.
Как известно из оптики, скорость передачи сигнала определяется не фазовой, а групповой скоростью волны (скоростью распространения волнового пакета) и определяется по формуле: υg = dω/dk. С помощью Е = ħω и p = ħk для волнового пакета имеем

Вычислим групповую скорость фотонов и нерелятивистских частиц. Для фотонов имеем

.

чего и следовало ожидать. Для нерелятивистских частиц найдем

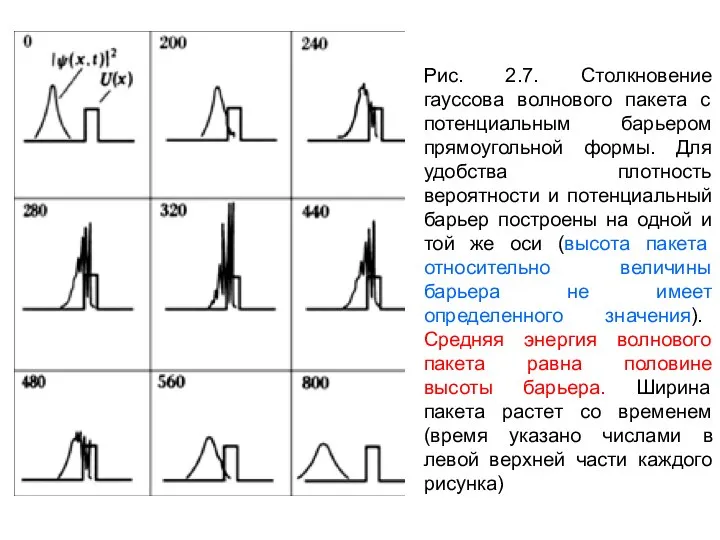
локализованной частицы в виде волнового пакета приводит к верному классическому результату, и волновой пакет перемещается со скоростью частицы.

коэффициенты А(k) определяют вклад различных волн де Бройля в рассматриваемую волновую функцию ψ(х,t); коэффициенты заметно отличны от нуля лишь для значений k, лежащих внутри интервала Δk вблизи некоторого k = k0.
Разброс Δх по координатам функции ψ(х,t) (ширина пакета) скоррелирован с разбросом Δk функции А(k) по волновым числам k: Δх⋅Δk ≥ 1/2.

Эволюция волнового пакета во времени предопределена, если для волновой функции ψ(х,t) известны А(k) и закон дисперсии волн − связь ω и k: ω = ω(k).
В вакууме связь между ω и k линейна: ω = сk, где с − скорость световых волн. Подставляя ω = сk в интеграл Фурье, получим

скоростью υg = dω/dk = с без изменения формы.
В случае произвольной связи ω = ω(k) зависимость ψ(х,t) имеет более сложный вид.
Рассмотрим две частицы, одна из которых имеет групповую скорость υg, а другая – скорость υg + Δυg. В момент времени t = 0 их координаты совпадают, а спустя промежуток времени t частицы расходятся на расстояние

Δх = (Δυg)t.
Покажем, что отдельному волновому пакету свойствен разброс значений групповой скорости Δυg, который приводит к увеличению его ширины Δх. Оценим величину Δυg:

величиной ħ/Δx0, где Δх0 – неопределенность начального положения или ширина исходного волнового пакета. Подставим Δр = ħ/Δx0 в выражение для Δvg:

Поскольку Δх = Δυg t, имеем

.

Подобного «расплывания» волнового пакета можно избежать, только поместив частицу в потенциальную яму. На рис. 2.6 показана деформация волнового пакета со временем, а на рис 2.7 – столкновение волнового пакета, описывающего свободную частицу, с потенциальным барьером.

Рис. 2.6. Расплывание волнового пакета с течением времени t. Гауссов волновой пакет в два последовательных момента времени. Пакет движется вправо с групповой скоростью, которая совпадает со скоростью частицы

Для удобства плотность вероятности и потенциальный барьер построены на одной и той же оси (высота пакета относительно величины барьера не имеет определенного значения). Средняя энергия волнового пакета равна половине высоты барьера. Ширина пакета растет со временем (время указано числами в левой верхней части каждого рисунка)

квантовая теория позволяет точно определить поведение волновой функции в будущем, если она известна в начальный момент времени, однако это мало чем может помочь, поскольку волновая функция очень быстро расплывается по всему пространству.

Оценим количественно скорость расплывания волнового пакета в случае свободной частицы. Рассмотрим свободный электрон, локализованный в начальный момент времени в области Δх0 = = 10–10 м (типичный размер атома). Спустя одну секунду,

из волн де Бройля, перемещается со скоростью классической частицы, явился иллюстрацией предельного перехода квантовомеханических законов движения к законам движения классической частицы по классической траектории. Аналогично факт расплывания волнового пакета со временем способствовал принятию статистической интерпретации квантовой механики (поскольку из него следовало, что квадрат модуля волновой функции нельзя рассматривать как плотность частицы).