Содержание
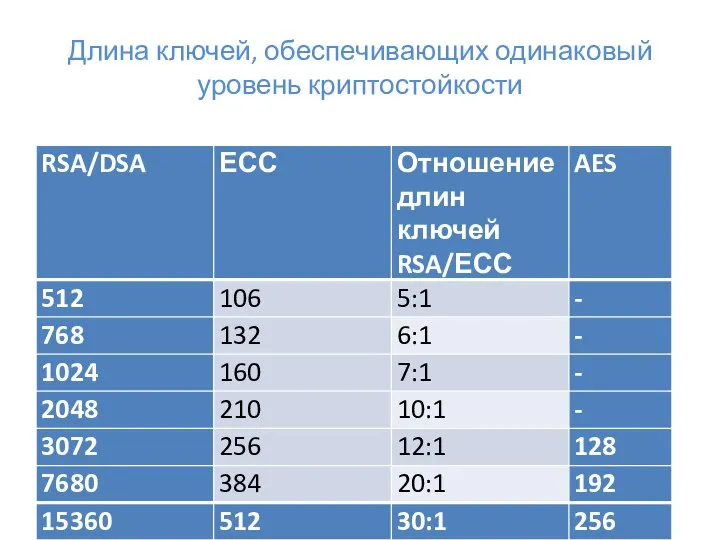
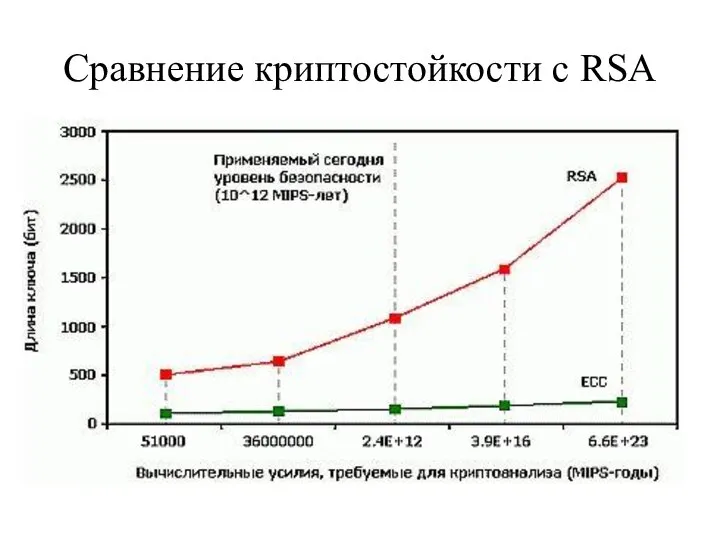
- 2. Длина ключей, обеспечивающих одинаковый уровень криптостойкости
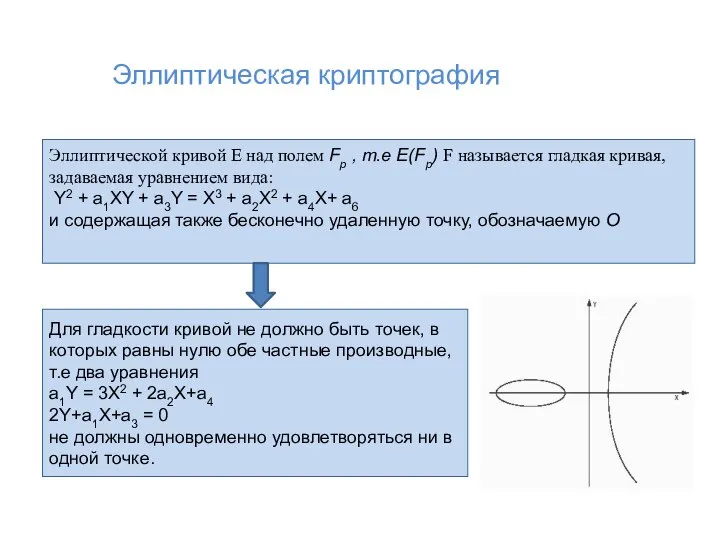
- 3. Эллиптической кривой Е над полем Fр , т.е E(Fp) F называется гладкая кривая, задаваемая уравнением вида:
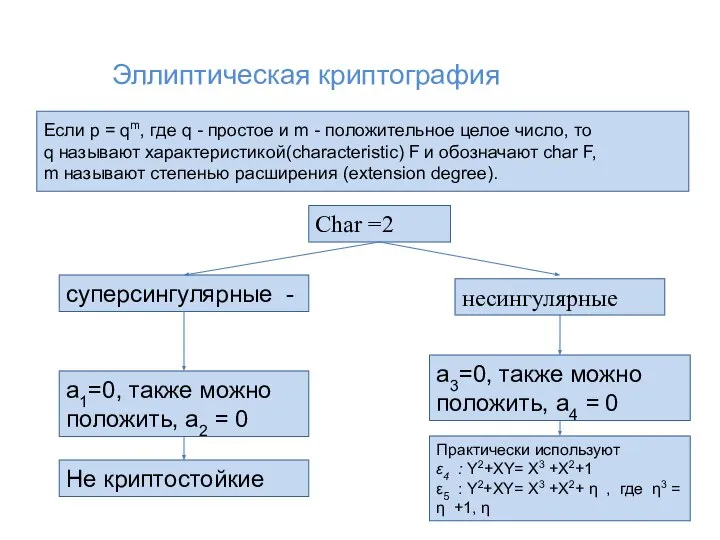
- 4. Если p = qm, где q - простое и m - положительное целое число, то q
- 5. Если Fp не является полем характеристики 2, то без потери общности можно полагать, что a1=a3= 0
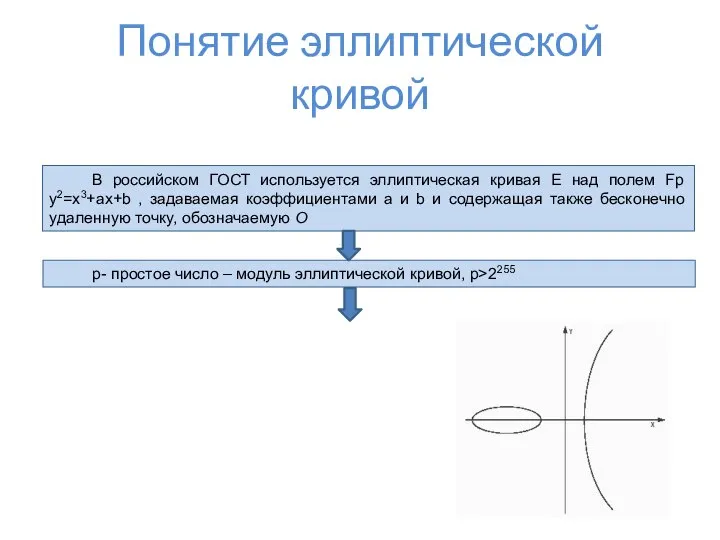
- 6. Понятие эллиптической кривой В российском ГОСТ используется эллиптическая кривая E над полем Fp y2=x3+ax+b , задаваемая
- 7. Понятие эллиптической кривой Множество точек эллиптической кривой вместе с нулевой точкой и с введенной операцией сложения
- 8. Понятие эллиптической кривой Точки эллиптической кривой могут складываться, но не могут умножаться. Однако возможно скалярное умножение,
- 9. Пусть P = (x1, y1) и Q = (x2, y2) две различные точки на кривой E.
- 10. Сложение точек на эллиптической кривой P + Q = R
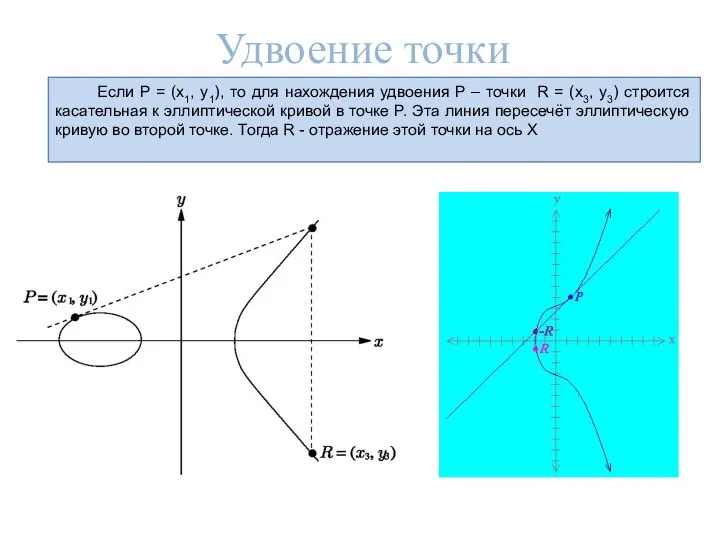
- 11. Удвоение точки Если P = (x1, y1), то для нахождения удвоения P – точки R =
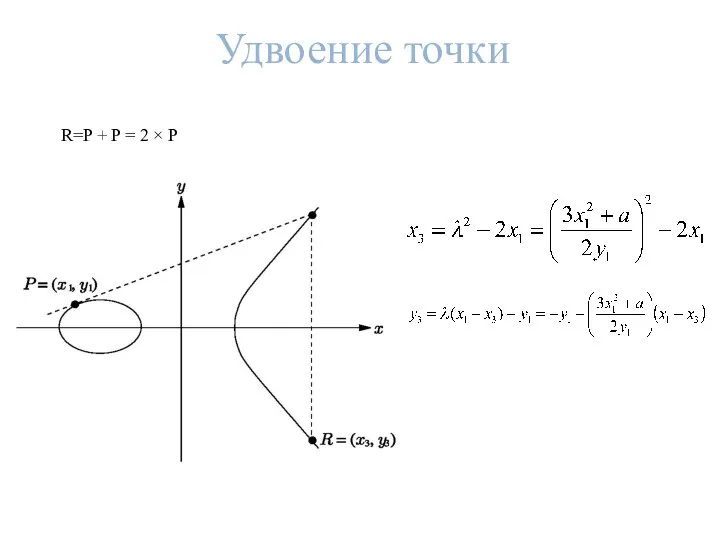
- 12. Удвоение точки R=P + P = 2 × P
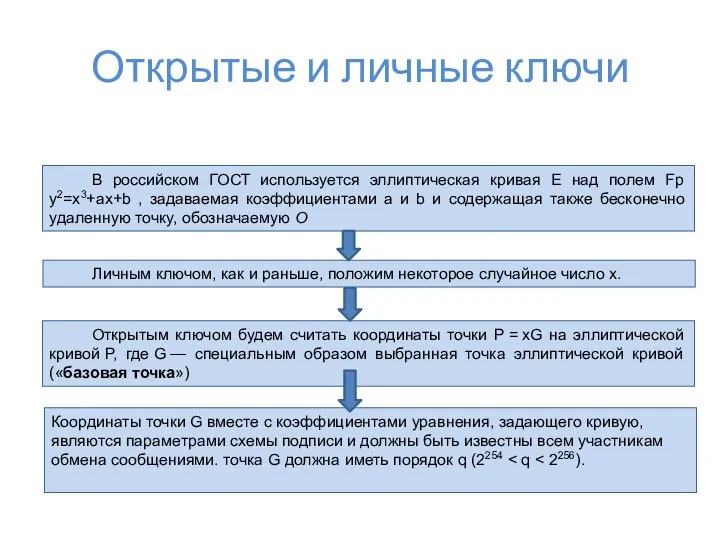
- 13. Открытые и личные ключи В российском ГОСТ используется эллиптическая кривая E над полем Fp y2=x3+ax+b ,
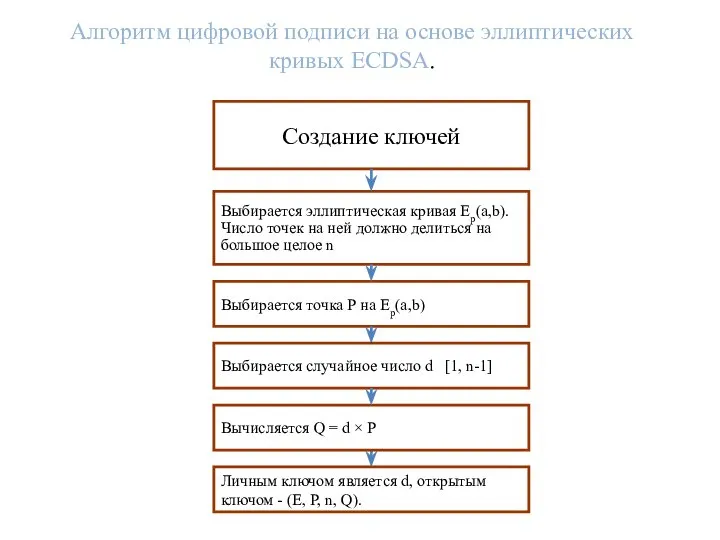
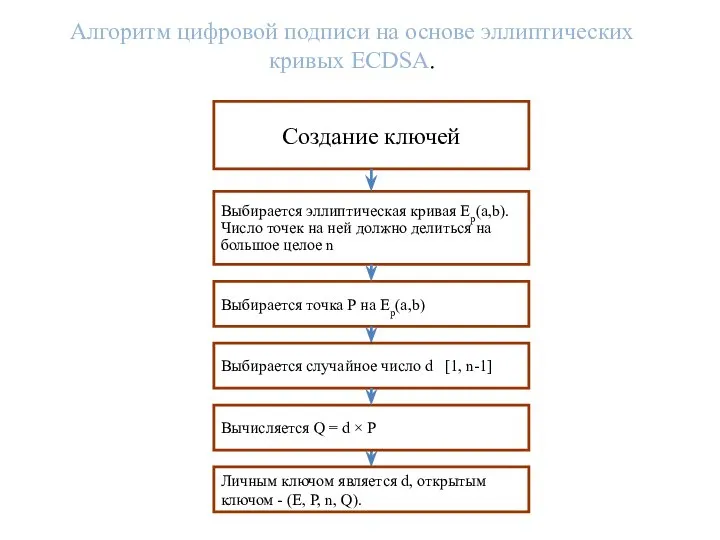
- 14. Алгоритм цифровой подписи на основе эллиптических кривых ECDSA. Создание ключей Выбирается эллиптическая кривая Ep(a,b). Число точек
- 15. Алгоритм цифровой подписи на основе эллиптических кривых ECDSA. Создание ключей Выбирается эллиптическая кривая Ep(a,b). Число точек
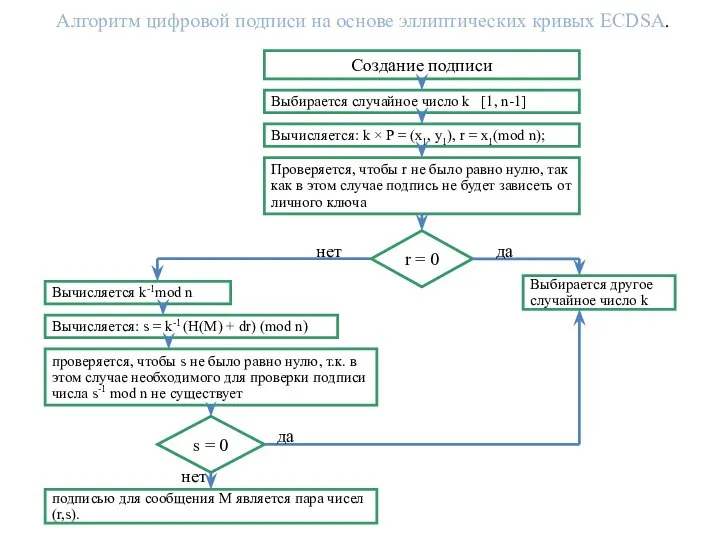
- 16. Алгоритм цифровой подписи на основе эллиптических кривых ECDSA. Создание подписи Выбирается случайное число k [1, n-1]
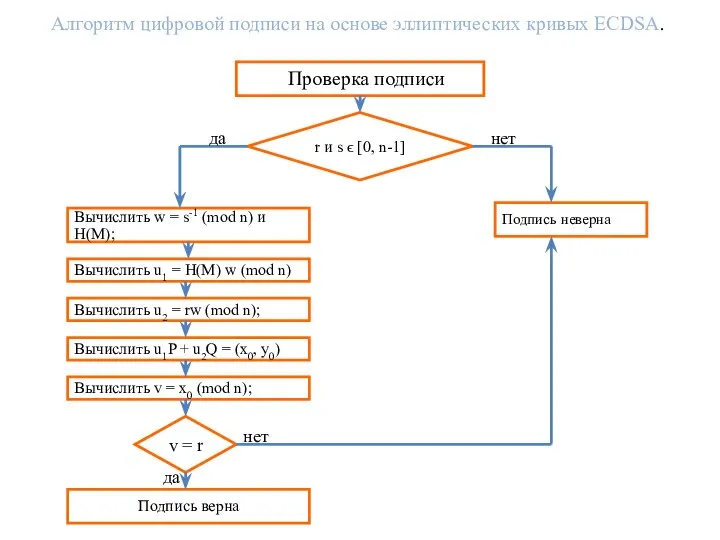
- 17. Алгоритм цифровой подписи на основе эллиптических кривых ECDSA. r и s ϵ [0, n-1] Подпись неверна
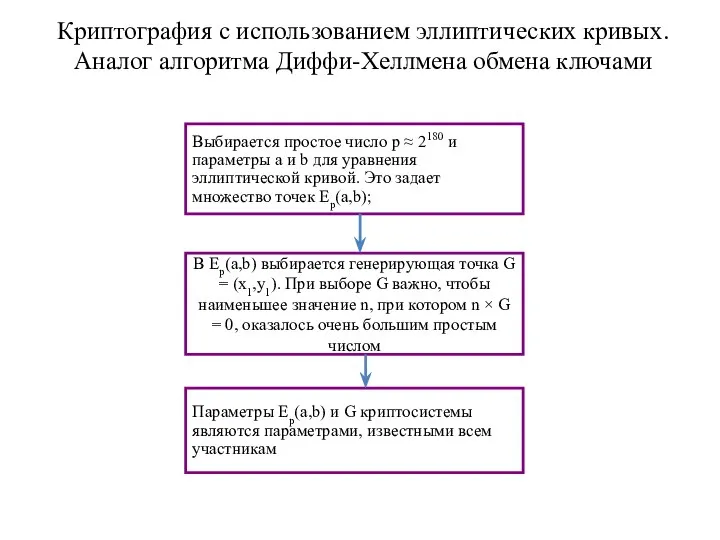
- 18. Криптография с использованием эллиптических кривых. Аналог алгоритма Диффи-Хеллмена обмена ключами Выбирается простое число р ≈ 2180
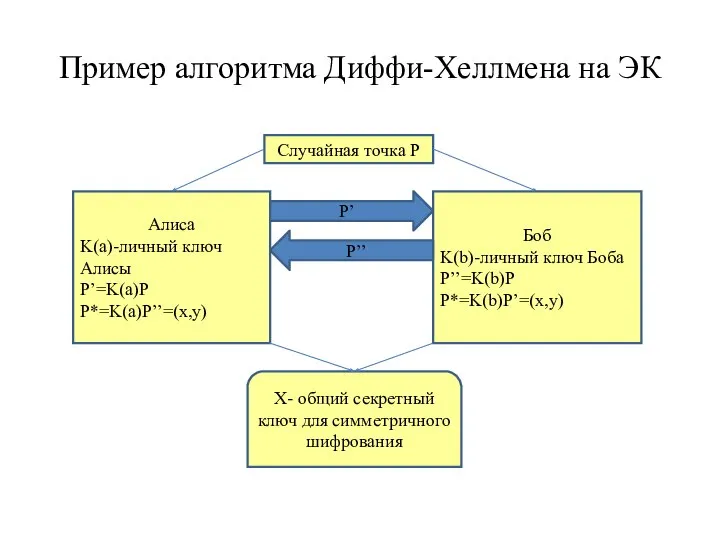
- 19. Пример алгоритма Диффи-Хеллмена на ЭК Алиса K(a)-личный ключ Алисы P’=K(a)P P*=K(a)P’’=(x,y) Боб K(b)-личный ключ Боба P’’=K(b)P
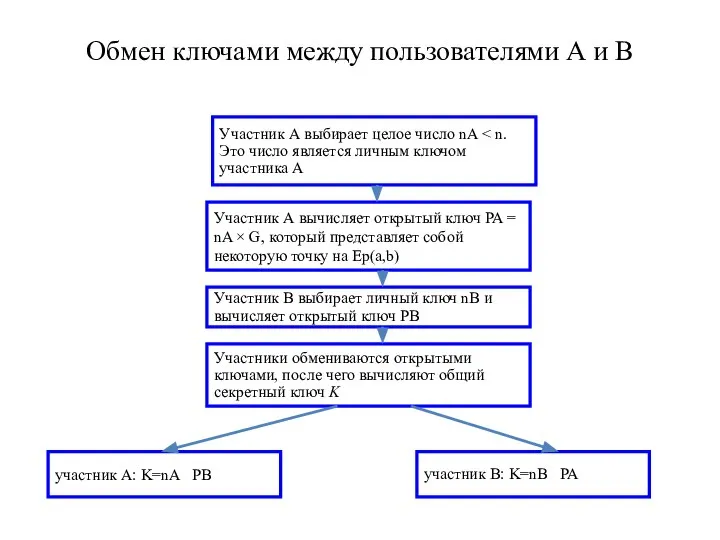
- 20. Участник А выбирает целое число nA Участник А вычисляет открытый ключ PA = nA × G,
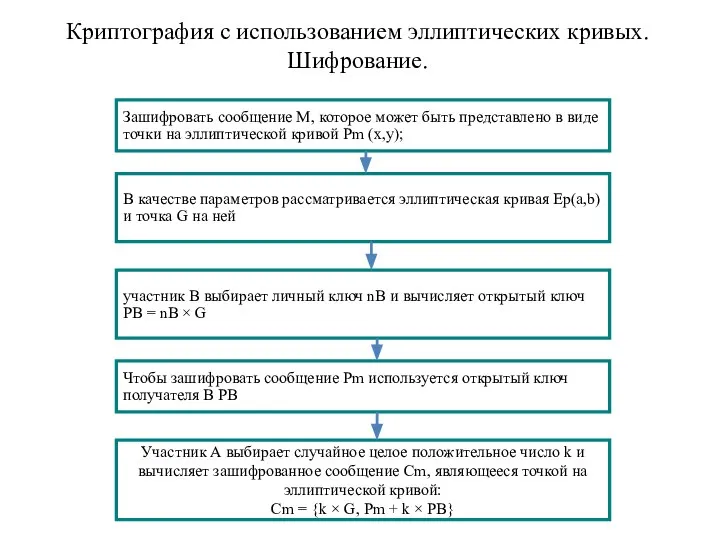
- 21. Зашифровать сообщение М, которое может быть представлено в виде точки на эллиптической кривой Pm (x,y); В
- 22. Участник В умножает первую координату точки на свой ЛК и вычитает результат из второй координаты: Pm
- 23. Сравнение криптостойкости с RSA
- 25. Скачать презентацию






 Эпидситуация по столбняку
Эпидситуация по столбняку  Презентация СРАВНИТЕЛЬНЫЙ АНАЛИЗ СОСТОЯНИЯ И РАЗВИТИЯ РЫНКОВ ТОРГОВЛИ МЕДИЦИНСКИМ ОБОРУДОВАНИЕМ В РОССИИ И ЗА РУБЕЖОМ
Презентация СРАВНИТЕЛЬНЫЙ АНАЛИЗ СОСТОЯНИЯ И РАЗВИТИЯ РЫНКОВ ТОРГОВЛИ МЕДИЦИНСКИМ ОБОРУДОВАНИЕМ В РОССИИ И ЗА РУБЕЖОМ  Викторина
Викторина Культура и личность
Культура и личность Бизнес план Кафе «Уютный дворик»
Бизнес план Кафе «Уютный дворик» Идентификация и обнаружение фальсификации продуктов животного происхождения
Идентификация и обнаружение фальсификации продуктов животного происхождения Инструменты и принадлежности сварщика
Инструменты и принадлежности сварщика Sales
Sales Тематический парк. 1С Hello Kitty. План по проекту
Тематический парк. 1С Hello Kitty. План по проекту Лексика языка Java
Лексика языка Java Sport tourism
Sport tourism Хаттама Хаттама
Хаттама Хаттама ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ РЫНКА ЦЕННЫХ БУМАГ Финансовая информация в деловой прессе Фондовые индексы Рейтинги ценных бума
ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ РЫНКА ЦЕННЫХ БУМАГ Финансовая информация в деловой прессе Фондовые индексы Рейтинги ценных бума Палитра души
Палитра души Инерциальные навигационные системы. (Тема 3)
Инерциальные навигационные системы. (Тема 3) Аортальные пороки (packed)
Аортальные пороки (packed) «Музеи в орбите учебно-воспитательного процесса в начальной школе: эффекты и феномены»
«Музеи в орбите учебно-воспитательного процесса в начальной школе: эффекты и феномены» Основные формы внеурочной физкультурно-спортивной деятельности
Основные формы внеурочной физкультурно-спортивной деятельности Экономическое развитие региона в условиях выхода из мирового финансового кризиса Конкурс творческих работ студентов гр. 44БД спе
Экономическое развитие региона в условиях выхода из мирового финансового кризиса Конкурс творческих работ студентов гр. 44БД спе Ұйымда жеке тұлғалық мінез-құлықтың ерекшелігі, когнитивті диссонанс
Ұйымда жеке тұлғалық мінез-құлықтың ерекшелігі, когнитивті диссонанс Вступ до спортивної морфології
Вступ до спортивної морфології Гетто Воркаут
Гетто Воркаут Здоровьесберегающие технологии
Здоровьесберегающие технологии Рисование в технике Граттаж
Рисование в технике Граттаж Статистический анализ энергетического рынка Европы
Статистический анализ энергетического рынка Европы Устами младенца - презентация для начальной школы_
Устами младенца - презентация для начальной школы_ Инженерная графика. Введение
Инженерная графика. Введение Анализ педагогической деятельности
Анализ педагогической деятельности