Содержание
- 2. Vzdělávací cíle Připravit model LP pro výpočet simplexovým algoritmem Sestavit výchozí simplexovou tabulku Nalézt optimální řešení
- 3. Model lineárního programování Cíl: nalézt vázaný extrém lineární funkce více proměnných, který vyhovuje daným lineárním omezujícím
- 4. Použité symboly a značení Proměnné x … strukturní proměnné; d … doplňkové proměnné; p … pomocné
- 5. Příklad Farma se rozhoduje o vyhrazení části své půdy pro pěstování pšenice, ječmene a žita. tyto
- 6. Simplexový algoritmus Splnění podmínek simplexového algoritmu Výchozí bázické řešení Test optima (vstupu) Test přípustnosti báze (výstupu)
- 7. Podmínky simplexového algoritmu Nezápornost složek vektoru pravých stran stačí zkontrolovat; pokud není splněna, lze příslušné omezující
- 8. Rovnicový tvar Nerovnice vyrovnáme na rovnice Doplňkové proměnné značíme d, indexujeme číslem omezující podmínky; přebírají jednotky
- 9. Kanonický tvar Nerovnice vyrovnáme na rovnice (doplňkové proměnné) Zajistíme úplnou jednotkovou submatici Pomocné proměnné značíme p,
- 10. Pomocné proměnné Přidáváme do omezujících podmínek požadavkových; typu určení; vždy s kladným znaménkem. Interpretace kolik jednotek
- 11. Výchozí bázické řešení Sestavení výchozí simplexové tabulky Identifikace bázických a nebázických proměnných Určení hodnot proměnných ve
- 12. Test optimality Existuje bázické řešení s lepší hodnotou ÚF? Záměna proměnných v bázi Koeficient zj –
- 13. Test přípustnosti I nové řešení musí splňovat podmínky SA Nezáporné složky vektoru b Známe klíčový sloupec
- 14. Nové řešení Jeden krok Jordanovy eliminační metody Přesun jednotkového vektoru pod proměnnou, která vstupuje do báze
- 15. Interpretace výsledku Rozdělení proměnných na bázické a nebázické Hodnoty všech proměnných Hodnota účelové funkce Relativní nevýhodnost
- 16. Shrnutí Pojem lineární optimalizační model Konstrukce simplexové tabulky Čtení v simplexové tabulce Optimalizace v simplexové tabulce
- 18. Скачать презентацию















 Система оптического распознавания документа
Система оптического распознавания документа  Организация, группа, коллектив
Организация, группа, коллектив История развития электроники
История развития электроники Типы молодежных субкультур
Типы молодежных субкультур Акулы (4 класс) - презентация для начальной школы_
Акулы (4 класс) - презентация для начальной школы_ Презентация Структурная деформация угольной промышленности
Презентация Структурная деформация угольной промышленности Концепция долгосрочного социально-экономического развития Российской Федерации
Концепция долгосрочного социально-экономического развития Российской Федерации Система права и система законодательства
Система права и система законодательства Презентация "ТЕАТР 17-18 ВЕКОВ" - скачать презентации по МХК
Презентация "ТЕАТР 17-18 ВЕКОВ" - скачать презентации по МХК Имидж Брянской области Концепция позиционирования региона в медийной, деловой и политической среде в 2012 г. Автор: Заровная
Имидж Брянской области Концепция позиционирования региона в медийной, деловой и политической среде в 2012 г. Автор: Заровная  Иисус Христос – реальная личность в истории
Иисус Христос – реальная личность в истории Принципы нанотехнологий
Принципы нанотехнологий Мечети Казани
Мечети Казани Испытательный срок Регламент
Испытательный срок Регламент  Сложение гармонических колебаний
Сложение гармонических колебаний  УРОК МАТЕМАТИКИ В 3 КЛАССЕ УЧИТЕЛЬ НАЧАЛЬНЫХ КЛАССОВ ШИШКАНОВА С.Е. КГБСКОУ СКШИ 8 ВИДА №11 «Подготовка к умножению»
УРОК МАТЕМАТИКИ В 3 КЛАССЕ УЧИТЕЛЬ НАЧАЛЬНЫХ КЛАССОВ ШИШКАНОВА С.Е. КГБСКОУ СКШИ 8 ВИДА №11 «Подготовка к умножению» Поступаем в платное учебное заведение Урок по основам потребительских знаний. Автор: Бабкина Т.Г учитель экономики МОУ Байнов
Поступаем в платное учебное заведение Урок по основам потребительских знаний. Автор: Бабкина Т.Г учитель экономики МОУ Байнов Управление программами и портфелями проектов
Управление программами и портфелями проектов  Михаил Юриевич Лермонтов Живот и творчество в картини Разр а ботил : М. Илиева. - презентация
Михаил Юриевич Лермонтов Живот и творчество в картини Разр а ботил : М. Илиева. - презентация Воскресная школа при Свято-Троицком храме г. Ирпень
Воскресная школа при Свято-Троицком храме г. Ирпень Художественная культура первой половины XIX века
Художественная культура первой половины XIX века Рынок земли
Рынок земли Имидж мастерская
Имидж мастерская Массовые формы культурно-досуговой деятельности
Массовые формы культурно-досуговой деятельности Процессор и память 2
Процессор и память 2 Конструктивні схеми каркасних багатоповерхових будівель
Конструктивні схеми каркасних багатоповерхових будівель Фен. Косметический девичник
Фен. Косметический девичник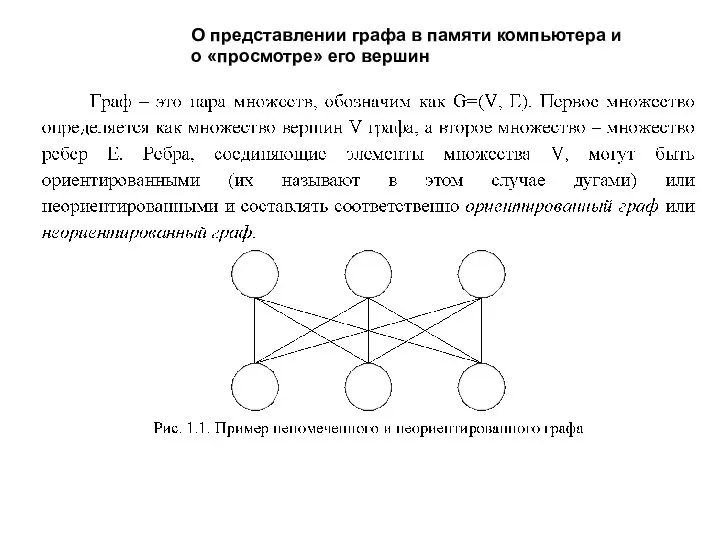 Поиски в графе
Поиски в графе