Содержание
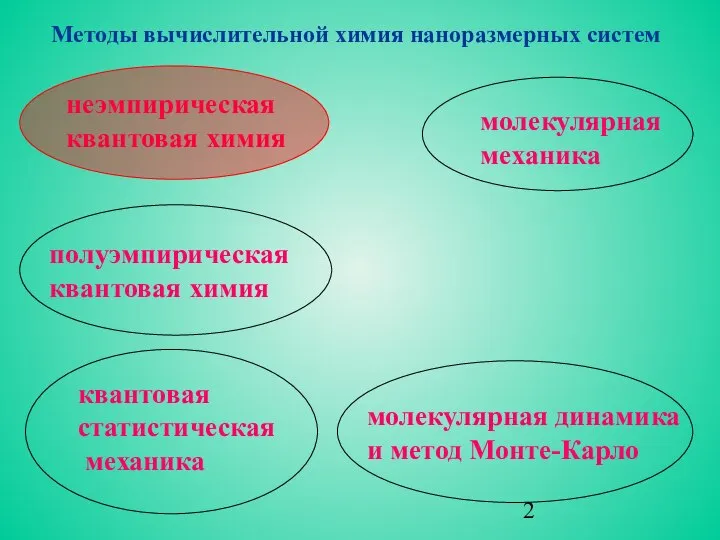
- 2. молекулярная динамика и метод Монте-Карло неэмпирическая квантовая химия полуэмпирическая квантовая химия квантовая статистическая механика молекулярная механика
- 3. Точное решение уравнения Шредингера для систем, имеющих более 2-х электронов невозможно, т.к. энергия взаимного отталкивания электронов
- 4. Гамильтониан атома с зарядом ядра Z|е| (начало координат на ядре): Исключим Vээ одноэлектронный гамильтониан Электрон i
- 5. Гамильтониан атома с зарядом ядра Z|е| (начало координат на ядре): Исключим Vээ одноэлектронный гамильтониан Электрон i
- 6. Полный гамильтониан атома в приближении независимых частиц Собственная функция Н (волновая функция Хартри) Энергия атома
- 7. Метод самосогласованного поля Межэлектронным отталкиванием не пренебрегают, но действие на данный электрон всех остальных электронов заменяют
- 8. Отталкивание между электронами i и j учтено дважды: как среднее по j и среднее по i
- 9. Как это сделать? Вероятность того, что электрон j с волновой функцией χj(rj) находится в бесконечно малом
- 10. Однако, чтобы вычислить этот интеграл, волновые функции должны уже быть известны! Задаются некоторым набором N одноэлектронных
- 11. Приближение центрального поля Потенциал дополнительно усредняют по всем направлениям, интегрируя его по углам θ и ϕ:
- 12. Атомные орбитали и их характеристики Решение радиального уравнения Шредингера конкретный вид которого возник после разделения переменных
- 13. Радиальные нормированные функции водородоподобных атомов Rnl (r)
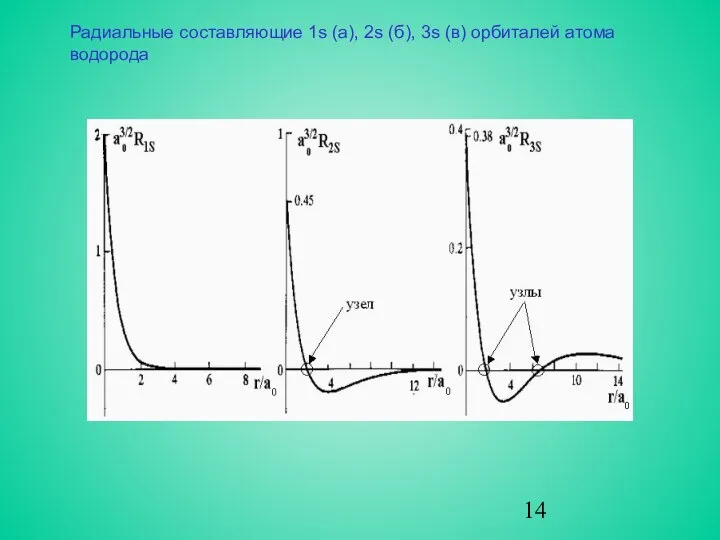
- 14. Радиальные составляющие 1s (а), 2s (б), 3s (в) орбиталей атома водорода
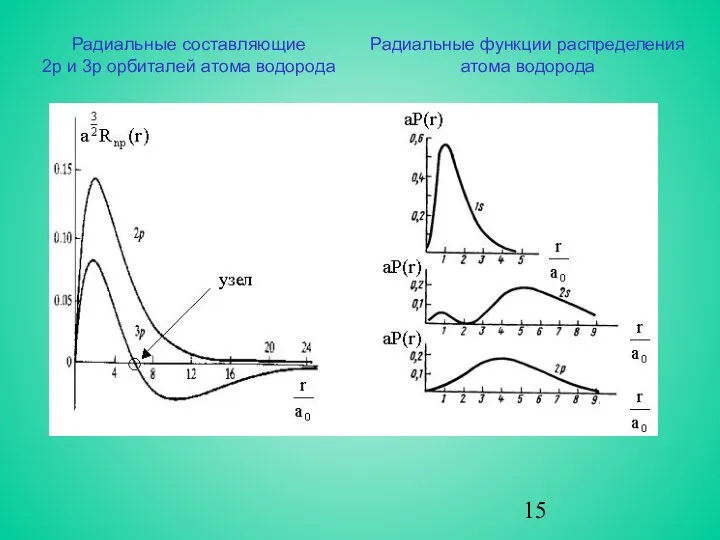
- 16. Основные свойства радиальных функций. 1) Как следствие свойств полиномов Лягерра радиальные функции с различными n и
- 17. Угловые функции Ylm (θ, ϕ) − собственные функции оператора квадрата углового момента L2 − описывают в
- 18. Угловые части волновой функции атома, обладающего центральным полем 1
- 19. Угловые части волновой функции атома, обладающего центральным полем
- 21. Скачать презентацию















 Воспитательная система класса Планета «Дружба»
Воспитательная система класса Планета «Дружба» Организация внеурочной деятельности в контексте требований ФГОС НОО
Организация внеурочной деятельности в контексте требований ФГОС НОО  Применение программного продукта MatLab для решения инженерной задачи
Применение программного продукта MatLab для решения инженерной задачи Личностный подход к лидерству. Теория черт.
Личностный подход к лидерству. Теория черт. Кинотеатр Калевала
Кинотеатр Калевала Lexikologie und Lexikographie
Lexikologie und Lexikographie История и традиции Новруз-байрама
История и традиции Новруз-байрама Правописание парных согласных в корне слова 2 класс
Правописание парных согласных в корне слова 2 класс Каток “Динамо” г. Киров
Каток “Динамо” г. Киров Первая помощь (1)
Первая помощь (1) Презентация Понятие и значение института реабилитации в уголовном судопроизводстве. Основания и условия реабилитации.
Презентация Понятие и значение института реабилитации в уголовном судопроизводстве. Основания и условия реабилитации. Методы культурологических исследований
Методы культурологических исследований Ренессанс и Реформация: в поисках новой личности.
Ренессанс и Реформация: в поисках новой личности. 21 февраля - международный день родного языка
21 февраля - международный день родного языка ВЕРИФИКАЦИЯ ПРОГРАММ ДВС
ВЕРИФИКАЦИЯ ПРОГРАММ ДВС сырым датұлы
сырым датұлы  Программирование циклических алгоритмов
Программирование циклических алгоритмов Лекция: «Экономика здравоохранения»
Лекция: «Экономика здравоохранения» Комбинаторные алгоритмы вычислительной геометрии Рандомизированный алгоритм построения выпуклой оболочки
Комбинаторные алгоритмы вычислительной геометрии Рандомизированный алгоритм построения выпуклой оболочки Соотношение кинетических и термодинамических параметров реакции
Соотношение кинетических и термодинамических параметров реакции  Спартак - презентация для начальной школы
Спартак - презентация для начальной школы Программирование на языке Java. Рекурсия
Программирование на языке Java. Рекурсия Программирование в среде MS Access
Программирование в среде MS Access Система законодательства об охране здоровья в Российской Федерации. Организация медицинской помощи населению
Система законодательства об охране здоровья в Российской Федерации. Организация медицинской помощи населению Сучасні інформаційні технології. Апаратні засоби мультимедіа
Сучасні інформаційні технології. Апаратні засоби мультимедіа Сосудистые заболевания головного мозга: механизмы развития, принципы патогенетической терапии
Сосудистые заболевания головного мозга: механизмы развития, принципы патогенетической терапии Ягоды тундры - презентация для начальной школы_
Ягоды тундры - презентация для начальной школы_ Эпоха возрождения
Эпоха возрождения