Содержание
- 2. молекулярная динамика и метод Монте-Карло неэмпирическая квантовая химия полуэмпирическая квантовая химия квантовая статистическая механика молекулярная механика
- 3. Антисимметричность многоэлектронной волновой функции Электроны обладают собственным моментом количества движения (спином), который в единицах ħ равен
- 4. Ни одна из них не является антисимметричной. Однако связанная с ними функция антисимметрична ( – нормировочный
- 5. Принцип Паули диктует, что две спин-орбитали с одинаковыми пространственными частями (т.е. с одинаковыми квантовыми числами n,
- 6. Заполнение электронами состояний любого атома происходит в порядке возрастания их энергий согласно принципа Паули и каждое
- 7. Детерминант Слейтера Электроны неразличимы, и их перестановка не меняет свойства системы; для волновой функции в виде
- 8. Метод Хартри-Фока Аппроксимация многоэлектронной волновой функции единственным детерминантом Слейтера и использование при ее нахождении ССП метод
- 9. Из условия минимума энергии возникает набор независимых уравнений для каждой одноэлектронной орбитали – уравнений Хартри-Фока: Энергия
- 10. Одноэлектронный интеграл описывает энергию электрона на орбитали в поле ядра без остальных электронов. Двухэлектронный кулоновский интеграл
- 11. Ограниченный и неограниченный методы Хартри-Фока Многоэлектронная волновая функция N-электронной системы должна быть антисимметричной и отвечать определенным
- 12. Собственные значения квадрата спинового момента электронов для разных спиновых состояний Пример - молекулы CH3 в дублетного
- 13. Метод Кона-Шэма Интегрирование проводится по пространственным координатам всех электронов, кроме одного, и по спинам всех электронов;
- 14. Минимизация функционала энергии относительно одноэлектронных функций χi(r) при дополнительном условии их ортонормировки и постоянства числа электронов
- 15. Квантово-химическая трактовка решений одноэлектронных уравнений Физический смысл ХФ энергии орбиталей εi имеют: если удалить с орбитали
- 16. Зависимость потенциалов ионизации элементов от атомного номера В пределах периода с увеличением атомного номера потенциалы ионизации
- 17. Приравнивая нулю дифференциал функционала электронной энергии d{E[ρ] – μN[ρ(r)]}Vяд = const = 0, (N = ∫
- 18. Зависимость энергии атома от числа электронов μ характеризует наклон кривой E = E(N). Производная в конечно-разностном
- 19. Определенная таким образом величина называется абсолютной электроотрицательностью (Parr, R. G. at all. 1978). Пирсон (1983), действуя
- 20. Можно также определить индекс электрофильности (Parr R. G. at all. 1999) = = , величина которого
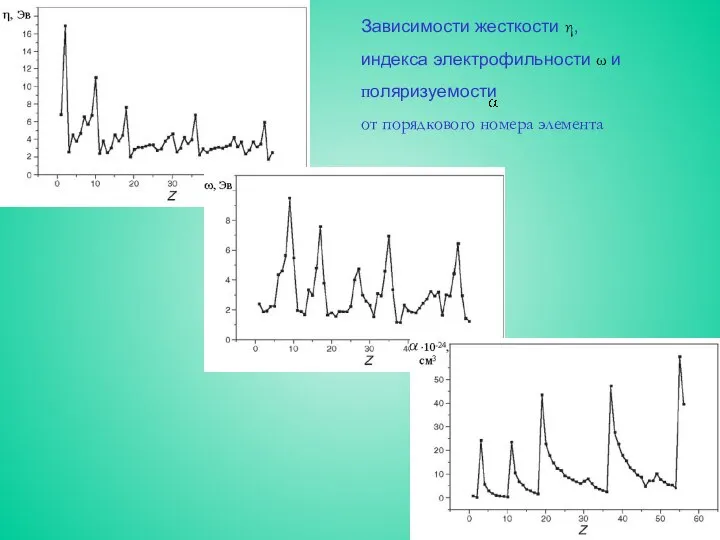
- 21. Зависимости жесткости η, индекса электрофильности ω и поляризуемости от порядкового номера элемента
- 22. Атомы с закрытыми оболочками или подоболочками имеют большую жесткость и малую поляризуемость . В каждом периоде
- 24. Скачать презентацию
молекулярная динамика
и метод Монте-Карло
неэмпирическая
квантовая химия
полуэмпирическая
квантовая химия
молекулярная динамика
и метод Монте-Карло
неэмпирическая
квантовая химия
полуэмпирическая
квантовая химия
квантовая
статистическая
механика
молекулярная
механика
Методы вычислительной химия наноразмерных систем
Антисимметричность многоэлектронной волновой функции
Электроны обладают собственным моментом количества движения (спином), который
Антисимметричность многоэлектронной волновой функции
Электроны обладают собственным моментом количества движения (спином), который
Наличие спина приводит к специальным ограничениям на электронную волновую функцию, известным как принцип Паули.
1.Электронная волновая функция системы из нескольких электронов должна быть антисимметричной (менять знак) относительно обмена положениями и спинами пары из любых двух электронов i и j:
2. Никакие два электрона не могут быть в одном и том же квантовом состоянии (принцип исключения).
(58)
.
Пример: атом гелия (2 электрона). Две эквивалентных волновых функции Хартри для этой системы имеют вид:
Ни одна из них не является антисимметричной. Однако связанная с ними
Ни одна из них не является антисимметричной. Однако связанная с ними
антисимметрична ( – нормировочный коэффициент).
Если мы попытаемся поместить электроны 1 и 2 на одну и ту же спин-орбиталь χi, то получим:
.
Значит, волновая функция в этом виде удовлетворяет принципу исключения Паули. С математической точки зрения волновая функция есть детерминант из спин-орбиталей χi(х):
.
Важным свойством детерминанта является то, что он меняет знак при перестановке двух любых его столбцов или строк; величина его при этом остается неизменной. Это эквивалентно перемене мест двух электронов: электрон 1 перемещается с орбитали i на орбиталь j, а электрон 2 – с орбитали j на орбиталь i. Если же два столбца или две строки детерминанта одинаковы (что эквивалентно занятию двумя электронами одной и той же орбитали), то детерминант равен нулю.
Принцип Паули диктует, что две спин-орбитали с одинаковыми пространственными частями (т.е.
Принцип Паули диктует, что две спин-орбитали с одинаковыми пространственными частями (т.е.
χi(x) = χi(r)η(s)
Рассмотрим атом Не. Из возможных вариантов распределения электронов по 1s и 2s АО атома Не основному состоянию соответствует схема а.
Волновая функция основного состояния:
где функция
Функция имеет симметричную пространственную часть и антисимметричную спиновую. Полный спин системы равен нулю, это состояние принято называть синглетным.
Заполнение электронами состояний любого атома происходит в порядке возрастания их энергий
Заполнение электронами состояний любого атома происходит в порядке возрастания их энергий
Состояния и соответствующие им АО с одинаковыми квантовыми числами n и l заполняются так, чтобы суммарный спин электронов был максимален (правило Хунда); сначала заполняется максимальное число АО с разными m.
Последовательность заполнения АО для нейтральных атомов в основном состоянии:
1s < 2s < 2p < 3s < 3p < 4s ~ 3d < 4p < 5s ~ 4d < 5p < 6s ~5d ~ 4f < 6p < 7s …
(aufbau-принцип, который служит обоснованием таблицы Менделеева.)
Порядок заполнения атомных орбиталей обусловлен не отношением их энергий, а требованием минимума полной энергии атома, которая отлична от суммы одноэлектронных энергий. Также играют роль спин-орбитальные и другие эффекты. Именно поэтому, в частности, 4s AO заполняются электронами в атомах K и Ca раньше, чем 3d АО.
Электроны с одним и тем же значением главного квантового числа n образуют электронные слои. Эти слои, в свою очередь, построены из оболочек (nl), заполненных электронами с одинаковым значением орбитального квантового числа l. Слои с n = 1,2,3,4,... обозначают буквами K, L, M, N,...
Детерминант Слейтера
Электроны неразличимы, и их перестановка не меняет свойства системы;
Детерминант Слейтера
Электроны неразличимы, и их перестановка не меняет свойства системы;
.
Детерминант Слейтера - единственная функция, обеспечивающая антисимметричность волновой функции, записанной через орбитали (орбитальное приближение). Следовательно, он дает только одно решение соответствующих одноэлектронных уравнений. Каждый электрон описывается "своей" волновой функцией.
Системы, в которых все электроны занимают орбитали попарно, называются системами с закрытыми (замкнутыми) электронными оболочками. Для таких систем детерминант Слейтера состоит из дважды занятых электронами орбиталей, число которых равно половине числа электронов. Системы с нечетным числом электронов называются системами с открытыми (незамкнутыми) оболочками.
Метод Хартри-Фока
Аппроксимация многоэлектронной волновой функции единственным детерминантом Слейтера и использование при
Метод Хартри-Фока
Аппроксимация многоэлектронной волновой функции единственным детерминантом Слейтера и использование при
Fi = + .
Здесь и далее мы используем принятую в квантовой химии атомную систему единиц: множитель опускается, m = 1, e = 1, ħ =1.
Различие между F и H состоит в том, что оператор кулоновского электронного взаимодействия заменен оператором в квадратных скобках, описывающим взаимодействие каждого электрона со средним полем всех остальных электронов с учетом требований принципа Паули.
Из условия минимума энергии возникает набор независимых уравнений для каждой одноэлектронной
Из условия минимума энергии возникает набор независимых уравнений для каждой одноэлектронной
Энергия электрона, находящегося на орбитали :
где
Полная энергия атома с замкнутыми электронными оболочками (по 2 электрона на каждой орбитали) в методе ХФ вычисляется следующим образом:
Одноэлектронный интеграл описывает энергию электрона на орбитали в поле ядра без
Одноэлектронный интеграл описывает энергию электрона на орбитали в поле ядра без
Оператор Фока сам зависит от полного набора одноэлектронных волновых функций и его решение ищется самосогласованно.
Наличие обменного члена в операторе Фока эквивалентно учету корреляции в движении электронов с одинаковыми спинами, связанных с разными орбиталями (обменной корреляции). Кулоновская корреляция, вызванная взаимным отталкиванием электронов независимо от их спинов, в методе ХФ не учитывается: это является следствием приближения независимых частиц и представляет собой существенный недостаток метода. Кроме того, в противоположность точной волновой функции однодетерминантная функция ХФ вследствие самосогласования не имеет сингулярности при ⎢ri – rj ⎢→ 0, следующей из вида потенциальной энергии межэлектронного взаимодействия. Уравнения ХФ могут в принципе быть решены численно любым стандартным методом решения интегрально-дифференциальных уравнений.
Ограниченный и неограниченный методы Хартри-Фока
Многоэлектронная волновая функция N-электронной системы должна
Ограниченный и неограниченный методы Хартри-Фока
Многоэлектронная волновая функция N-электронной системы должна
Когда волновая функция аппроксимируется единственным детерминантом Слейтера, состоящим из таких спин-орбиталей, метод называется ограниченным (по спину) методом Хартри-Фока (ОХФ).
Если же требование быть собственной функцией S2 на волновую функцию не накладывается, метод называется неограниченным методом ХФ (НХФ),
Волновая функция атома Li в ограниченном и неограниченном методе Хартри-Фока
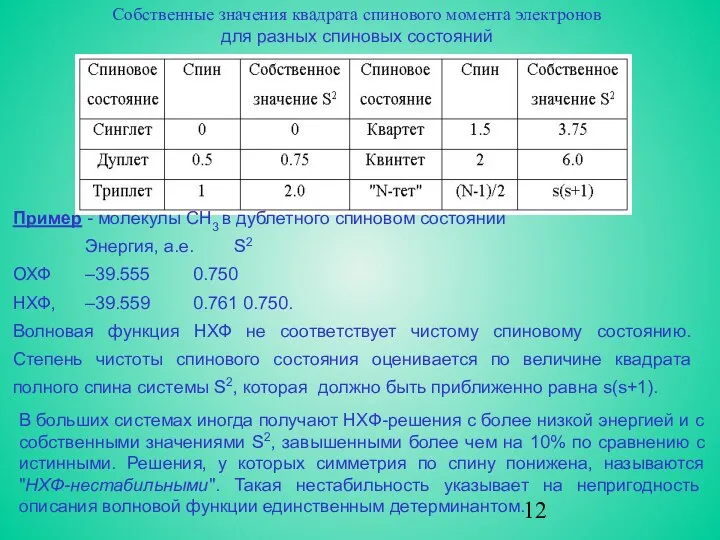
Собственные значения квадрата спинового момента электронов
для разных спиновых состояний
Пример -
Собственные значения квадрата спинового момента электронов
для разных спиновых состояний
Пример -
Энергия, а.е. S2
ОХФ –39.555 0.750
НХФ, –39.559 0.761 0.750.
Волновая функция НХФ не соответствует чистому спиновому состоянию. Степень чистоты спинового состояния оценивается по величине квадрата полного спина системы S2, которая должно быть приближенно равна s(s+1).
В больших системах иногда получают НХФ-решения с более низкой энергией и с собственными значениями S2, завышенными более чем на 10% по сравнению с истинными. Решения, у которых симметрия по спину понижена, называются "НХФ-нестабильными". Такая нестабильность указывает на непригодность описания волновой функции единственным детерминантом.
Метод Кона-Шэма
Интегрирование проводится по пространственным координатам всех электронов, кроме одного,
Метод Кона-Шэма
Интегрирование проводится по пространственным координатам всех электронов, кроме одного,
Электронная энергия системы зависит от ρ(r) следующим образом:
Многоэлектронная волновая функция Ψ({x}) связана с электронной плотностью (ЭП)
основного состояния :
ρ(r=r1) = Ψ*({x})Ψ({x})dr2dr3…ds1ds2ds3…
где – потенциал ядер, а G[ρ] – функционал ЭП, представляющий собой сумму кинетической энергии и неклассической энергии электрон-электронного взаимодействия, связанной с обменом и корреляцией электронов. Теорема Хоэнберга-Кона утверждает, что G[ρ] – одинаковый для всех многоэлектронных систем (универсальный) функционал электронной плотности, причем, точная ЭП основного состояния обеспечивает минимум функционала. Теория, которая изучает способы расчета электронной структуры молекул и кристаллов, основываясь на минимизации этого функционала, называется теорией функционала плотности (ТФП).
Минимизация функционала энергии относительно одноэлектронных функций χi(r) при дополнительном условии их
Минимизация функционала энергии относительно одноэлектронных функций χi(r) при дополнительном условии их
, i=1,2,3,…
где ρ = χi 2, – электростатический потенциал, создаваемый ядрами,
– обменно-корреляционный потенциал, Exc[ρ] – зависящая от электронной плотности обменно-корреляционная энергия.
Эта система уравнений решается методом ССП и заменяет в ТФП одноэлектронные уравнения Хартри-Фока. Все приближения связаны со способами аппроксимации обменно–корреляционного потенциала .
Энергии одноэлектронных состояний:
εi(ТФП) = ,
(ni – электронная заселенность состояния i); в методе Хартри-Фока они равны разности энергий двух состояний с числом электронов, отличающимся на единицу:
εi(ХФ) = EХФ[ni = 1] – EХФ[ni = 0].
Квантово-химическая трактовка решений
одноэлектронных уравнений
Физический смысл ХФ энергии орбиталей εi имеют: если
Квантово-химическая трактовка решений
одноэлектронных уравнений
Физический смысл ХФ энергии орбиталей εi имеют: если
Этот результат называется теоремой Купманса. Обитальные ХФ-энергии дают оценку потенциалов ионизации I - энергий, которые необходимо сообщить системе, чтобы удалить какой-либо из ее электронов, она характеризует прочности связи электрона данной орбитали с атомным остовом.
Первый потенциал ионизации I1 описывает энергию отрыва электрона с высшей занятой атомной орбитали. При этом и исходный атом, и образовавшийся ион находятся в основных (невозбужденных) состояниях. Потенциалы ионизации I2, I3, I4 и т.д. отвечают дальнейшим последовательным отрывам электронов от ионов,
I1 < I2 < I3
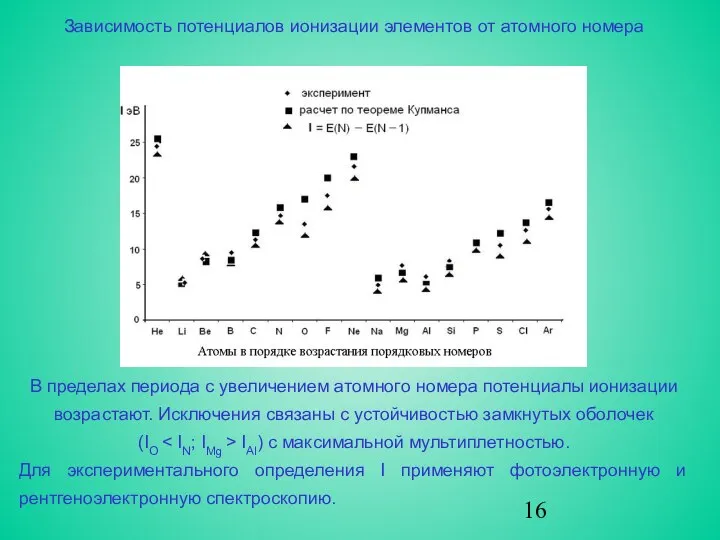
Зависимость потенциалов ионизации элементов от атомного номера
В пределах периода с
Зависимость потенциалов ионизации элементов от атомного номера
В пределах периода с
(IО < IN; IMg > IAl) с максимальной мультиплетностью.
Для экспериментального определения I применяют фотоэлектронную и рентгеноэлектронную спектроскопию.
Приравнивая нулю дифференциал функционала электронной энергии d{E[ρ] – μN[ρ(r)]}Vяд = const
Приравнивая нулю дифференциал функционала электронной энергии d{E[ρ] – μN[ρ(r)]}Vяд = const
(N = ∫ ρ(r) dv), можно определить электронный химический потенциал μ:
При образовании химической системы из атомов химический потенциал выравнивается, при этом происходит переток электронов к атому с большим значением μ. По смыслу это совпадает с введенной Полингом электроотрицательностью.
Использование теоремы Купманса оправдано для молекул с жесткой структурой (для сопряженных углеводородов и др.), не изменяющих свою геометрию при ионизации. Более точно потенциал ионизации следует вычислять как разность ХФ энергий атома (молекулы) с замкнутой оболочкой и образующегося иона:
I1 = E(N) – E(N–1)
Сродством к электрону Ax называют энергию, которая высвобождается при присоединении к нейтральному атому одного электрона.
A1 = E(N+1) – E(N),
Cродство к электрону можно приближенно охарактеризовать энергией низшей свободной (виртуальной) АО.
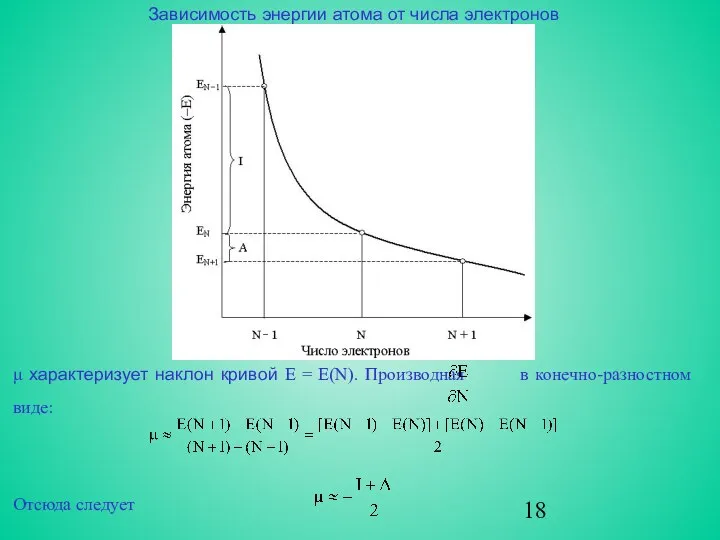
Зависимость энергии атома от числа электронов
μ характеризует наклон кривой E =
Зависимость энергии атома от числа электронов
μ характеризует наклон кривой E =
Отсюда следует
Определенная таким образом величина
называется абсолютной электроотрицательностью (Parr, R. G. at all.
Определенная таким образом величина
называется абсолютной электроотрицательностью (Parr, R. G. at all.
Пирсон (1983), действуя аналогичным образом, показал, что скорость изменения химического потенциала μ при изменении числа электронов N есть абсолютная химическая жесткость
В рамках метода Хартри-Фока атомная жесткость есть
η = (ЕНСАО – ЕВЗАО),
где ЕНСАО – энергия нижней свободной атомной орбитали; ЕВЗАО – энергия высшей занятой атомной орбитали.
Можно также определить индекс электрофильности (Parr R. G. at all. 1999)
Можно также определить индекс электрофильности (Parr R. G. at all. 1999)
величина которого может использоваться как индекс склонности атома (молекулы) к атаке электрофила. Другой важный индекс – поляризуемость , которая представляет собой меру линейного отклика электронной плотности в присутствии бесконечно малого электрического поля F и представляет собой вторую производную от энергии:
Экспериментально наблюдаемое значение поляризуемости является усредненным по координатам:
Величины , , ω и α являются характеристиками для атомов, ионов, молекул, других многоэлектронных многоядерных систем. Они лежат в основе концепций принципа жестких и мягких кислот и оснований, принципа максимальной жесткости, предложенного Пирсоном, и принципа минимальной поляризуемости, предложенным Chattaraj, P. K.; Poddar, A. J., 1998.
Зависимости жесткости η,
индекса электрофильности ω и
поляризуемости
от порядкового номера элемента
Зависимости жесткости η,
индекса электрофильности ω и
поляризуемости
от порядкового номера элемента
Атомы с закрытыми оболочками или подоболочками имеют большую жесткость и малую
Атомы с закрытыми оболочками или подоболочками имеют большую жесткость и малую
Наиболее электроотрицательные элементы обладают максимальной электрофильностью ω, и наоборот.
Для легких атомов главных подгрупп отношение приблизительно постоянно и для них электроотрицательность может рассматриваться как хорошая мера относительной электрофильности в пределах группы. Отметим ωF > ωCl и χF > χCl, однако F < Cl.
В общем случае поляризуемость уменьшается по периоду и увеличивается в группе с ростом Z. Для η и ω наблюдается обратная тенденция. В зависимостях η и ω от Z, структура электронных подоболочек проявляется более отчетливо.












![Приравнивая нулю дифференциал функционала электронной энергии d{E[ρ] – μN[ρ(r)]}Vяд = const](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1297931/slide-16.jpg)



 Основы технологии оклейки стен обоями
Основы технологии оклейки стен обоями По статистике* женщины с маленькой грудью 18 раз в день думают, что большая грудь позволит им найти любимого. - презентация
По статистике* женщины с маленькой грудью 18 раз в день думают, что большая грудь позволит им найти любимого. - презентация Литературная викторина Автор презентации Клюквина В А
Литературная викторина Автор презентации Клюквина В А Свойства некоторых аналоговых фильтров
Свойства некоторых аналоговых фильтров  Types of houses
Types of houses Визуальная система программирования Delphi. Язык программирования Object Pascal
Визуальная система программирования Delphi. Язык программирования Object Pascal СМИ в избирательных процессах
СМИ в избирательных процессах Как выбрать подрядчика по контекстной рекламе: преимущества и недостатки самостоятельного ведения
Как выбрать подрядчика по контекстной рекламе: преимущества и недостатки самостоятельного ведения  Грех и его трактовка в разных религиях
Грех и его трактовка в разных религиях Взаимное положение прямых
Взаимное положение прямых Презентация Жизнь и творчество И.С, Баха
Презентация Жизнь и творчество И.С, Баха А. Т. Аверченко 1881-1925
А. Т. Аверченко 1881-1925 Личное и групповое туристское снаряжение и уход за ним. Индивидуальный и групповой ремонтный набор
Личное и групповое туристское снаряжение и уход за ним. Индивидуальный и групповой ремонтный набор Экскурсия по Афинам
Экскурсия по Афинам INTEL - INTegrated circuits and ELectronics
INTEL - INTegrated circuits and ELectronics Расчет системы охлаждения
Расчет системы охлаждения  Периодизация развития художественной культуры. Стили эпохи
Периодизация развития художественной культуры. Стили эпохи Беседа по картине В.М. Васнецова «Богатыри» Автор: Сосновцева Валентина Николаевна – учитель начальных классов МОУ «СОШ с. Елшанк
Беседа по картине В.М. Васнецова «Богатыри» Автор: Сосновцева Валентина Николаевна – учитель начальных классов МОУ «СОШ с. Елшанк «Роль характера взаимоотношений между родителями и детьми в развитии личности ребенка»
«Роль характера взаимоотношений между родителями и детьми в развитии личности ребенка» Разработка сетевых приложений
Разработка сетевых приложений Исследование развития скоростных способностей у школьников 13-14 лет на уроках баскетбола
Исследование развития скоростных способностей у школьников 13-14 лет на уроках баскетбола Построение топографического плана по результатам нивелирования по квадратам
Построение топографического плана по результатам нивелирования по квадратам УЧЕТ РАСХОДОВ ПО СТРОИТЕЛЬНЫМ МАШИНАМ И МЕХАНИЗМАМ
УЧЕТ РАСХОДОВ ПО СТРОИТЕЛЬНЫМ МАШИНАМ И МЕХАНИЗМАМ Личность педагога в современной школе Личность воспитателя значит все в деле воспитания К.Д Уш
Личность педагога в современной школе Личность воспитателя значит все в деле воспитания К.Д Уш Презентация "1 ВВЕДЕНИЕ В МАКРОЭКОНОМИКУ" - скачать презентации по Экономике
Презентация "1 ВВЕДЕНИЕ В МАКРОЭКОНОМИКУ" - скачать презентации по Экономике Семейное увлечение хоккей
Семейное увлечение хоккей Traditions and holidays of Great Britain
Traditions and holidays of Great Britain Полезные ископаемые Презентацию подготовила Сковородина Елена Павловна, учитель начальны
Полезные ископаемые Презентацию подготовила Сковородина Елена Павловна, учитель начальны