Содержание
- 2. Берман Г.Н. Сборник задач по курсу математического анализа: учеб пособие. СПб.: Лань, 2007. – 448 с.
- 3. §1. Непрерывность функции 1.1. Непрерывность функции в точке и на множестве 1.2. Точки разрыва функции и
- 4. §1. Непрерывность функции 1.1. Непрерывность функции в точке и на множестве
- 5. §1. Непрерывность функции (продолжение)
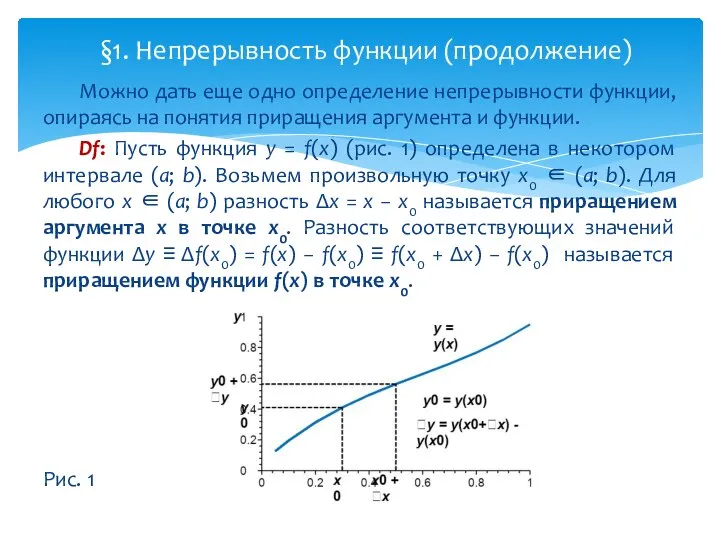
- 6. Можно дать еще одно определение непрерывности функции, опираясь на понятия приращения аргумента и функции. Df: Пусть
- 7. §1. Непрерывность функции (продолжение)
- 8. §1. Непрерывность функции (продолжение)
- 9. §1. Непрерывность функции (продолжение)
- 10. 1.2. Точки разрыва функции и их классификация
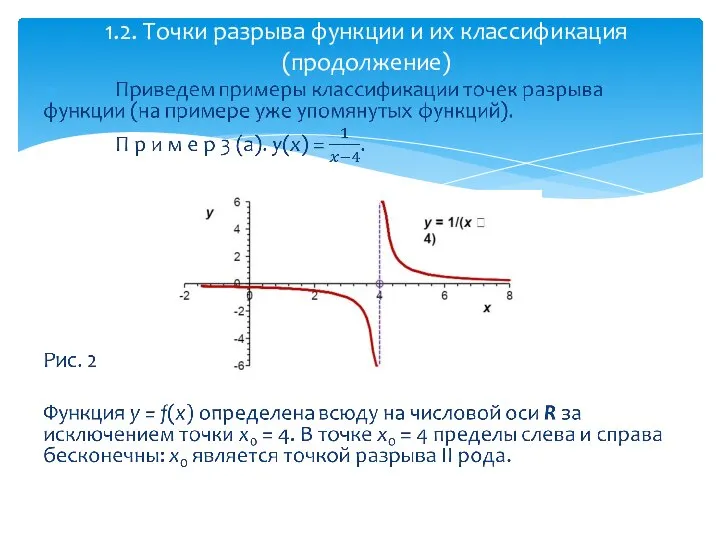
- 11. 1.2. Точки разрыва функции и их классификация (продолжение)
- 12. 1.2. Точки разрыва функции и их классификация (продолжение)
- 13. П р и м е р 3 (б). y(x) = sgn(x). Рис. 3 Функция y =
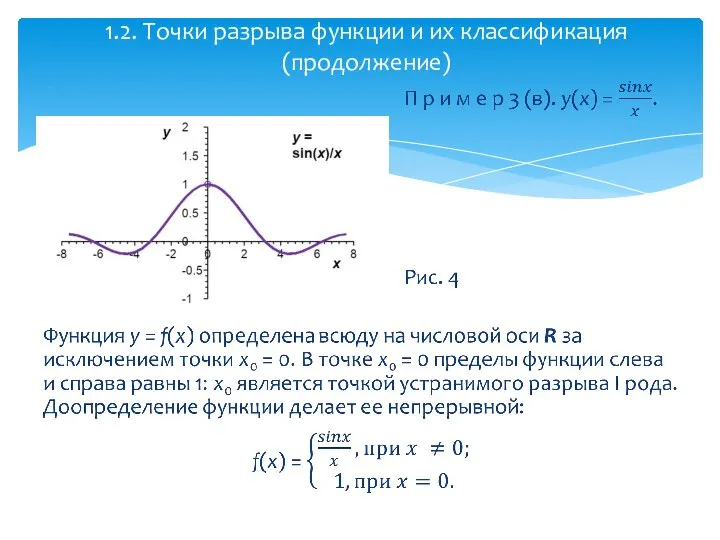
- 14. 1.2. Точки разрыва функции и их классификация (продолжение)
- 15. §2. Непрерывные функции и их свойства 2.1. Основные теоремы о непрерывных функциях
- 16. 2.1. Основные теоремы о непрерывных функциях (продолжение)
- 17. Т е о р е м а 3. Функция, обратная к непрерывной функции, есть функция непрерывная.
- 18. Df: Элементарной функцией называется такая функция, которую можно задать одной формулой, содержащей конечное число арифметических действий
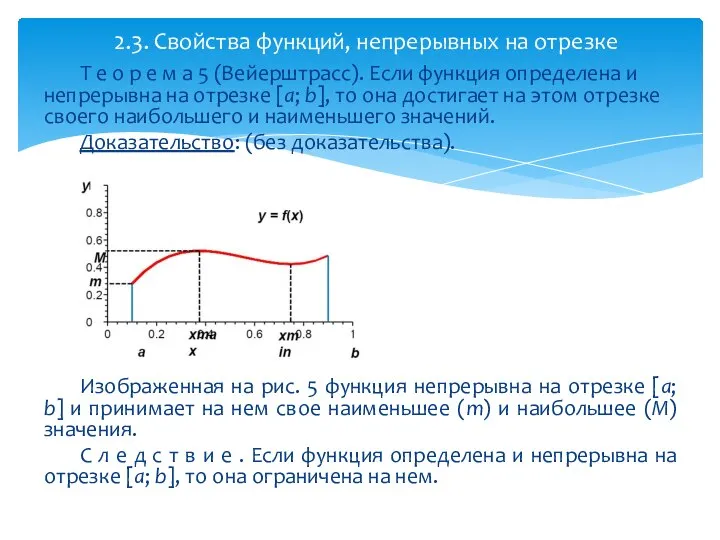
- 19. Т е о р е м а 5 (Вейерштрасс). Если функция определена и непрерывна на отрезке
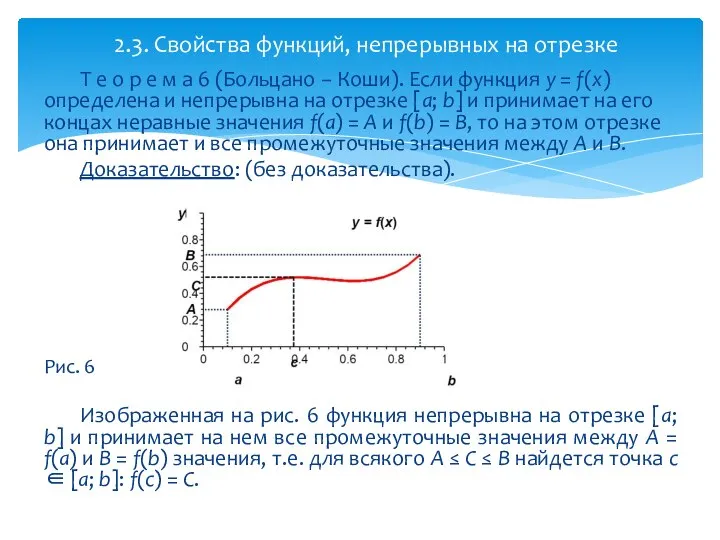
- 20. Т е о р е м а 6 (Больцано − Коши). Если функция y = f(x)
- 21. С л е д с т в и е из теоремы 6. Если функция y =
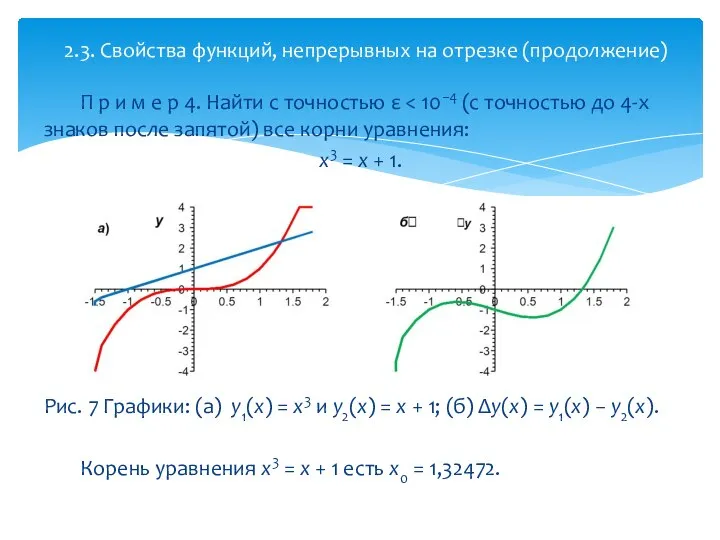
- 22. П р и м е р 4. Найти с точностью ε x3 = x + 1.
- 24. Скачать презентацию















 Введение в профессию. Тест-драйв профессии веб дизайнер
Введение в профессию. Тест-драйв профессии веб дизайнер Кәсіпкерлік қызмет субъектілерінің жауапкершілігі. (Тақырып 9)
Кәсіпкерлік қызмет субъектілерінің жауапкершілігі. (Тақырып 9) Рецепт. Структура рецепта. Обозначение лекарственных веществ и их количества (пропись). Правила прописи. Союзы в рецепте
Рецепт. Структура рецепта. Обозначение лекарственных веществ и их количества (пропись). Правила прописи. Союзы в рецепте (« Один дома »)Все стихи из этой книжки Для девчонок и мальчишек, Книжку эту прочитай Да на ус себе мотай: Как вести, когда ты дома, Ка
(« Один дома »)Все стихи из этой книжки Для девчонок и мальчишек, Книжку эту прочитай Да на ус себе мотай: Как вести, когда ты дома, Ка Решение задач
Решение задач  Информационно-измерительная система пирометрического типа для малоразмерного беспилотного летательного аппарата (бпла)
Информационно-измерительная система пирометрического типа для малоразмерного беспилотного летательного аппарата (бпла) Патологически привычные действия
Патологически привычные действия Научно-исследовательская работа по теме: «Фальсификация алкогольной продукции» Выполнили: студенты 2 курса очной формы обучени
Научно-исследовательская работа по теме: «Фальсификация алкогольной продукции» Выполнили: студенты 2 курса очной формы обучени Инфраструктура обеспечения бизнеса Выполнили: Хропина Ольга и Фунтикова Виктория
Инфраструктура обеспечения бизнеса Выполнили: Хропина Ольга и Фунтикова Виктория Обобщение знаний о глаголе_
Обобщение знаний о глаголе_ Презентация Процессуальные ошибки прокурора
Презентация Процессуальные ошибки прокурора Выполнила: студентка 3-го курса ФТД группы Т-083 Восколович Юля _
Выполнила: студентка 3-го курса ФТД группы Т-083 Восколович Юля _ Система психологической и коррекционной работы тренера как условие адаптации к спортивной жизни
Система психологической и коррекционной работы тренера как условие адаптации к спортивной жизни Грамматикалық категориялар
Грамматикалық категориялар Эссенциальная гипертензия
Эссенциальная гипертензия  Субкультуры или кто во что горазд «Каждому – свое» Надпись на воротах Бухенвальда Бухенвальд — немецкий концентрационный лаге
Субкультуры или кто во что горазд «Каждому – свое» Надпись на воротах Бухенвальда Бухенвальд — немецкий концентрационный лаге TianDe (ТианДе)
TianDe (ТианДе) Теория Эдварда Холла о контекстах культуры. Теория культурных измерений Герта Хофстеде
Теория Эдварда Холла о контекстах культуры. Теория культурных измерений Герта Хофстеде Основные понятия и определения теории телетрафика
Основные понятия и определения теории телетрафика Проблема апраксий
Проблема апраксий  Особенности работы с КД в электронной форме
Особенности работы с КД в электронной форме  Резные кружева. Русская домовая резьба
Резные кружева. Русская домовая резьба Задание: реализовать класс валидации (Java)
Задание: реализовать класс валидации (Java) Zahlen
Zahlen Актуальные вопросы кардиопрофилактики
Актуальные вопросы кардиопрофилактики Балуан Шолаќтыѕ 150 жылдыќ мерейтойына арналєан
Балуан Шолаќтыѕ 150 жылдыќ мерейтойына арналєан Мониторинг окружающей среды
Мониторинг окружающей среды Роль родителя в жизни школы “Чтобы узнать ребенка, надо хорошо знать его семью” В.А.Сухомлинский
Роль родителя в жизни школы “Чтобы узнать ребенка, надо хорошо знать его семью” В.А.Сухомлинский