Содержание
- 2. Неравенства Неравенство Маркова. Для любой случайной величины ξ и для любого ε > 0
- 3. Доказательство.
- 4. Неравенство Чебышёва Для любой случайной величины ξ и для любого ε >0
- 5. Доказательство В неравенстве Маркова (1) подставим вместо ξ ξ –Mξ и возьмем k=2.
- 6. Пример применения неравенства Чебышёва Оценить вероятность того, что сл.в. отклонится от своего матожидания на величину ≥
- 7. Неравенства Неравенство Коши – Буняковского – Шварца.
- 8. Сходимость по вероятности Определение. Последовательность случайных величин ξ1, ξ2 ,…, ξn сходится по вероятности к сл.
- 9. Сходимость по вероятности Обозначение: Замечание: «p» есть сокращение от «probability»
- 10. Пример Последовательность случайных величин ξ1, ξ2 ,…, ξn задана законом:
- 11. Закон больших чисел (ЗБЧ) Определение. Говорят, что к последовательности случайных величин ξ1, ξ2 ,…, ξn с
- 12. Смысл: среднее значение случайных величин стремится по вероятности к среднему их матожиданий (то есть, к постоянной
- 13. ЗБЧ в форме Чебышёва Теорема. Если для последовательности случайных величин {ξn} с математическими ожиданиями Mξi=ai и
- 14. Доказательство основано на неравенстве Чебышёва. Надо показать, что выполняется определение сходимости по вероятности.
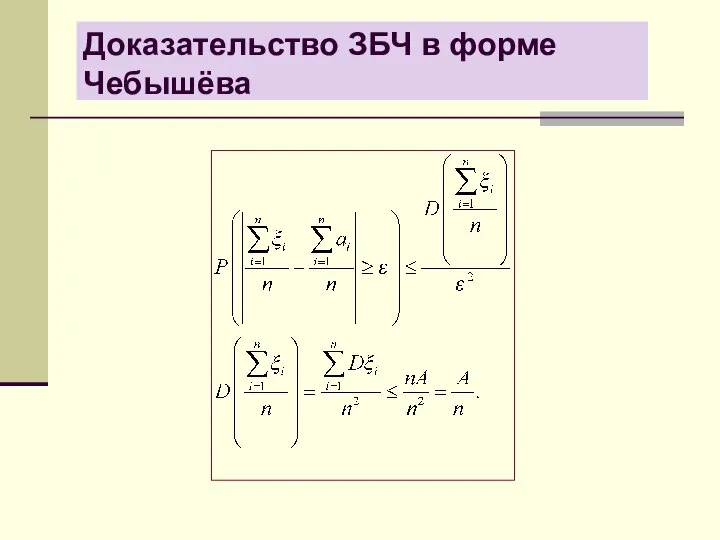
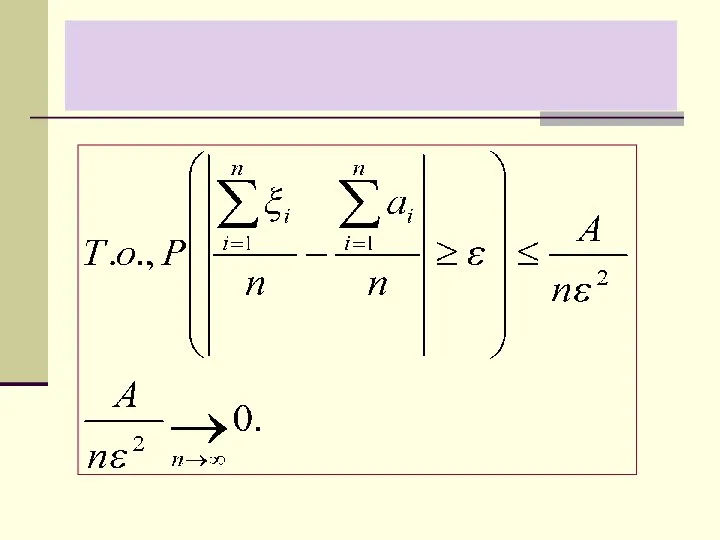
- 15. Доказательство ЗБЧ в форме Чебышёва
- 17. ЗБЧ в форме Бернулли Теорема. Пусть осуществляется серия из n независимых опытов, проводимых по схеме Бернулли
- 18. Доказательство ЗБЧ в форме Бернулли Рассмотрим случайную величину ξi, равную числу успехов в i –ом испытании,
- 19. ai = Mξi = p. Таким образом, (*) можно записать в виде (**), что представляет из
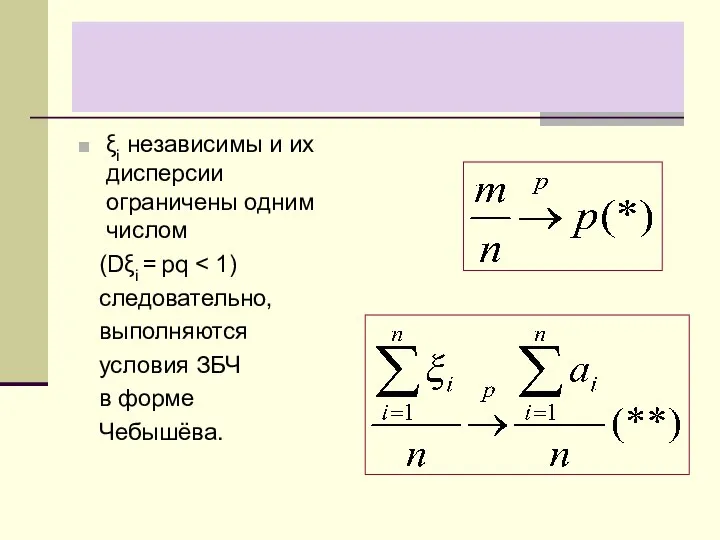
- 20. ξi независимы и их дисперсии ограничены одним числом (Dξi = pq следовательно, выполняются условия ЗБЧ в
- 21. ЗБЧ в форме Пуассона Теорема. Пусть осуществляется серия из n независимых опытов, причем вероятность успеха в
- 22. Доказательство ЗБЧ в форме Пуассона Рассмотрим случайную величину ξi, равную числу успехов в i–м испытании, i
- 23. ЗБЧ в форме Хинчина Теорема. Для того, чтобы к последовательности случайных величин {ξn} был применим ЗБЧ,
- 24. Центральная предельная теорема (ЦПТ) В теоремах этой группы выясняются условия, при которых возникает нормальное распределение. Общим
- 25. Центральная предельная теорема для независимых одинаково распределенных сл. в. Если случайные величины {ξn} независимы, одинаково распределены
- 26. Смысл ЦПТ для н.о.р.сл.в. Закон распределения суммы достаточно большого числа независимых одинаково распределенных случайных величин приближается
- 27. ЦПТ Теорема Ляпунова. Если случайная величина ξ представляет собой сумму большого числа независимых случайных величин ξ1,
- 28. Смысл ЦПТ в форме Ляпунова Закон распределения суммы достаточно большого числа независимых случайных величин, каждая из
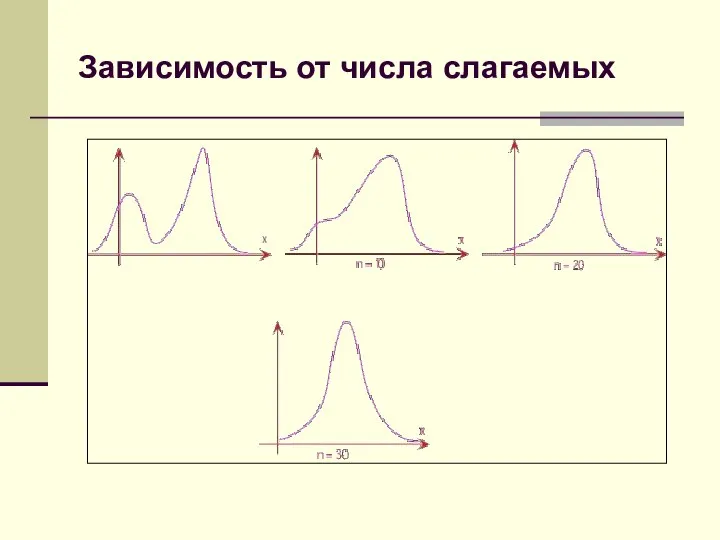
- 29. Зависимость от числа слагаемых
- 30. Практическое значение ЦПТ Многие случайные величины можно рассматривать как сумму отдельных независимых слагаемых. Например: ошибки различных
- 32. Скачать презентацию

























 Презентация Показания
Презентация Показания Презентация "Архитектурный облик религиозных центров Магнитогорска" - скачать презентации по МХК
Презентация "Архитектурный облик религиозных центров Магнитогорска" - скачать презентации по МХК Вирустар
Вирустар Образовательная технология «Портфолио»
Образовательная технология «Портфолио» ЭПОХА ВОЗРОЖДЕНИЯ
ЭПОХА ВОЗРОЖДЕНИЯ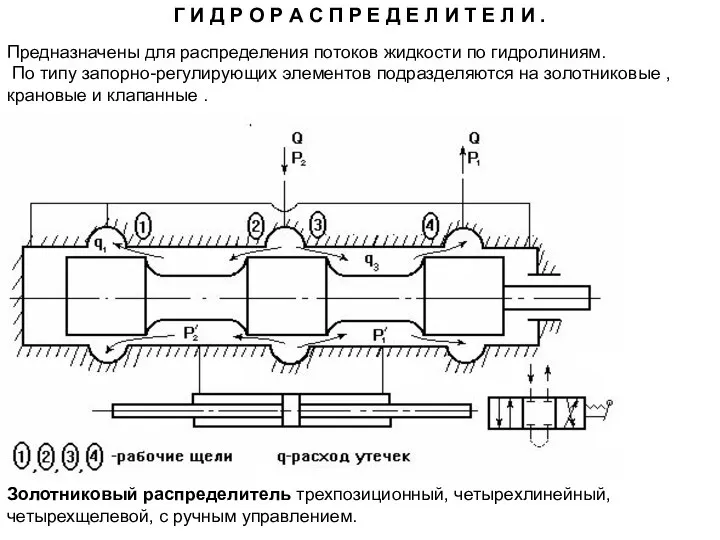 Гидрораспределители
Гидрораспределители  ДЕНЬГИ И ИХ РОЛЬ В ЭКОНОМИКЕ
ДЕНЬГИ И ИХ РОЛЬ В ЭКОНОМИКЕ  Определители и способы их вычисления
Определители и способы их вычисления  Велоклуб #велоннгасу
Велоклуб #велоннгасу Схемы электрооборудования автомобилей
Схемы электрооборудования автомобилей Построение дерева целей
Построение дерева целей УЗКИЙ ТАЗ в современном акушерстве
УЗКИЙ ТАЗ в современном акушерстве  Добро пожаловать в ознакомительный курс для соискателей компании «Smarter». Презентации вакансии
Добро пожаловать в ознакомительный курс для соискателей компании «Smarter». Презентации вакансии Морфология, репродукция, методы культивирования и индикации вирусов
Морфология, репродукция, методы культивирования и индикации вирусов Личность и политика
Личность и политика Юсуповы в истории России
Юсуповы в истории России Презентация по экономике Тема: НАЦИОНАЛЬНАЯ ЭКОНОМИКА
Презентация по экономике Тема: НАЦИОНАЛЬНАЯ ЭКОНОМИКА  Политическая идеология
Политическая идеология Формирование грамматических навыков
Формирование грамматических навыков  Иерархия потребностей по Маслоу
Иерархия потребностей по Маслоу Условия соревнований по виду «Спортивное ориентирование» (ориентирование по выбору)
Условия соревнований по виду «Спортивное ориентирование» (ориентирование по выбору) Отношения и пропорции - презентация по Алгебре
Отношения и пропорции - презентация по Алгебре Мезолит. Наскальная живопись из грота Ла Аранья. Сбор меда
Мезолит. Наскальная живопись из грота Ла Аранья. Сбор меда Соединение и выделение уголовных дел. Понятие и сущность.
Соединение и выделение уголовных дел. Понятие и сущность. Экспозиция — количество света попадающего на матрицу фотоаппарата в единицу времени
Экспозиция — количество света попадающего на матрицу фотоаппарата в единицу времени Общая характеристика философии Возрождения
Общая характеристика философии Возрождения Оснащение ВСП Московского банка кнопками вызова для маломобильных групп населения
Оснащение ВСП Московского банка кнопками вызова для маломобильных групп населения Презентация "Грим, визажистика и прическа в современной жизни" - скачать презентации по МХК
Презентация "Грим, визажистика и прическа в современной жизни" - скачать презентации по МХК