Содержание
- 2. Математическая статистика – это раздел математики который занимается разработкой методов сбора, описания и анализа экспериментальных результатов
- 3. В МС предполагается, что вероятность Р в модели наблюдаемого случайного явления не известна полностью. Известно только,
- 4. Задача математической статистики уменьшить неопределенность модели, используя информацию полученную из наблюдаемых исходов эксперимента. Итак, о математической
- 5. Основные понятия Исходным материалом всякого статистического исследования является совокупность результатов наблюдений. В большинстве случаев исходные статистические
- 6. Основные понятия Совокупность наблюдаемых случайных величин Х = (Х1, ..., Хn) называется выборкой, сами величины Xi
- 7. Пусть X = {х} – множество всех возможных значений выборки X, которое называется выборочным пространством. Статистической
- 8. Обычно рассматривают ситуации, когда компоненты выборки независимы и распределены так же, как некоторая случайная величина ξ
- 9. Таким образом, мы рассматриваем генеральную совокупность как случайную величину ξ, а выборку – как n –
- 10. Порядковые статистики Упорядочим выборку x = (x1, ..., xn) (реализацию) по возрастанию, получим последовательность x* =
- 11. Порядковые статистики Очевидно, что порядковые статистики удовлетворяют неравенствам X1*≤ X2* ≤ … ≤ Xn* X1* и
- 12. Способы представления выборки Вариационным рядом выборки называется способ ее записи, при котором элементы упорядочиваются по величине,
- 13. Способы представления выборки Статистическим рядом называется последовательность пар (xj,nj). Здесь xj – значения, а nj –
- 14. Группированный статистический ряд
- 15. Эмпирическая функция распределения Пусть Х=(X1, ..., Хn) – выборка из генеральной совокупности наблюдаемой случайной величины. Эмпирической
- 16. Пример Выборка: X = {1, 2, 2, 3}
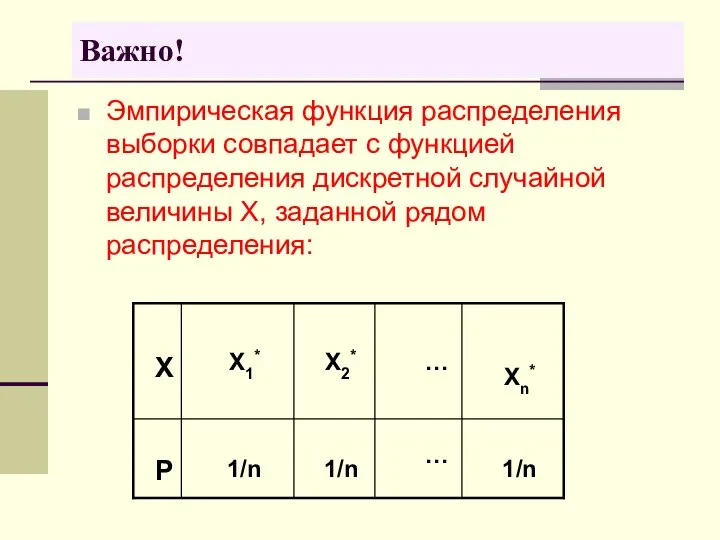
- 17. Эмпирическая функция распределения выборки совпадает с функцией распределения дискретной случайной величины X, заданной рядом распределения: Важно!
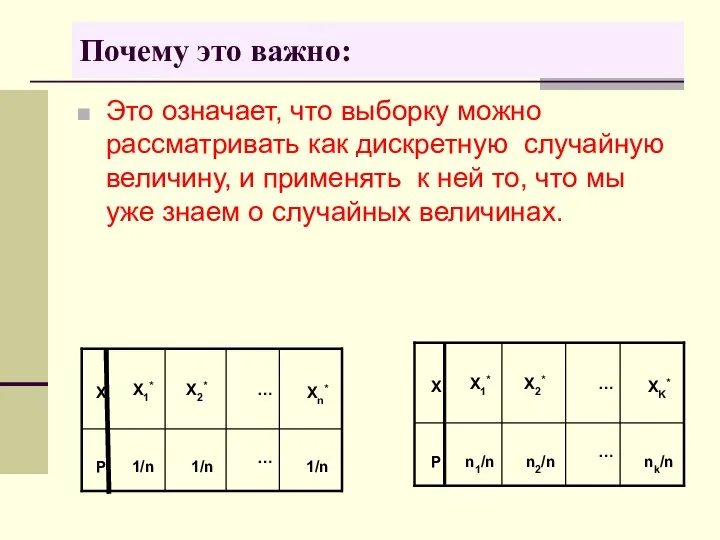
- 18. Почему это важно: Это означает, что выборку можно рассматривать как дискретную случайную величину, и применять к
- 19. Еще один пример
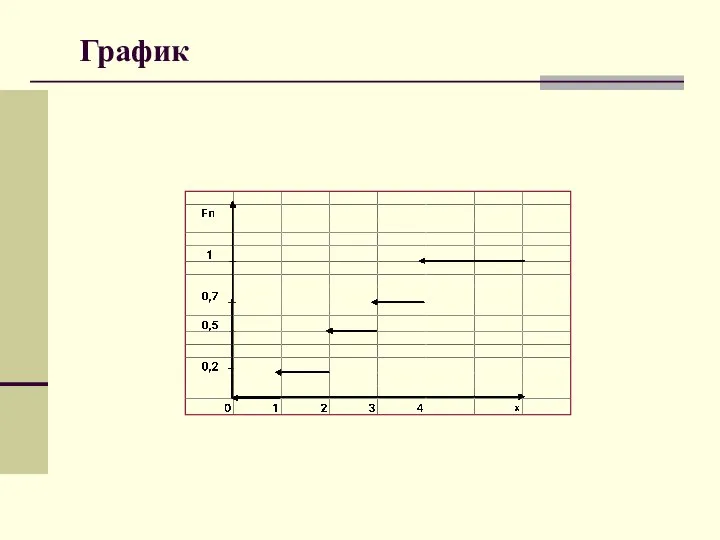
- 20. График
- 21. Общая запись эмпирической функции распределения
- 22. Замечание По эмпирической функции распределения легко построить другие способы представления выборки, например, статистический или вариационный ряд.
- 23. Пример
- 24. Этой эмпирической функции распределения Fn(x) соответствует выборка, заданная статистическим рядом: Пример
- 25. Задача. Дана Fn(x) из предыдущего примера. Сколько в выборке значений: а) равных 15, б) не больших
- 26. Свойства эмпирической функции распределения Эмпирическая функция распределения – сжатая характеристика выборки. Для каждой реализации х =
- 27. Свойства эмпирической функции распределения Пусть Fn(x) – эмпирическая функция распределения, построенная по выборке Х из распределения
- 28. Теорема 1 Пусть Fn(x) – эмпирическая функция распределения, построенная по выборке Х из распределения ξ, и
- 29. Теорема 2 (теорема Колмогорова) Если функция F(x) непрерывна, то при любом фиксированном t > 0 где
- 30. Теорема Колмогорова Теорема справедлива для любой непрерывной функции и позволяет найти границы, в которых с заданной
- 31. Частота элемента выборки При большом объеме выборки ее элементы объединяют в группы, представляя результаты опытов в
- 32. Группированный статистический ряд Вспомним вид этого ряда. Чтобы его построить, надо найти число интервалов k и
- 33. Группировка выборки Разность между максимальным и минимальным элементами выборки называется размахом выборки R. Число интервалов k
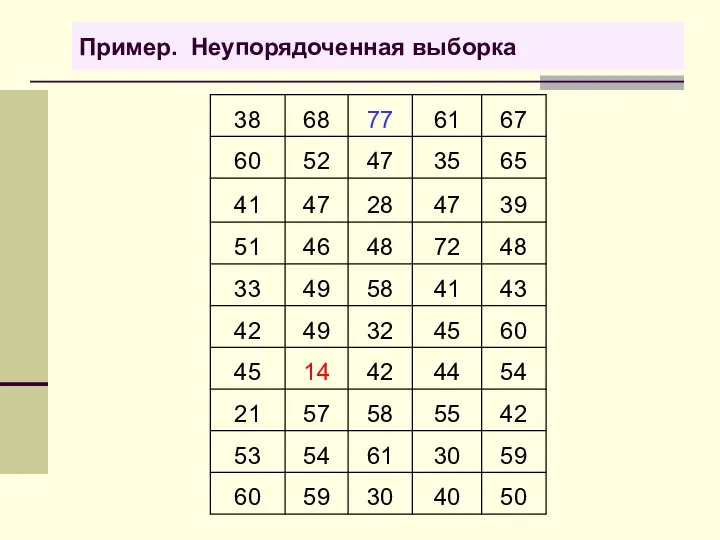
- 34. Пример. Неупорядоченная выборка
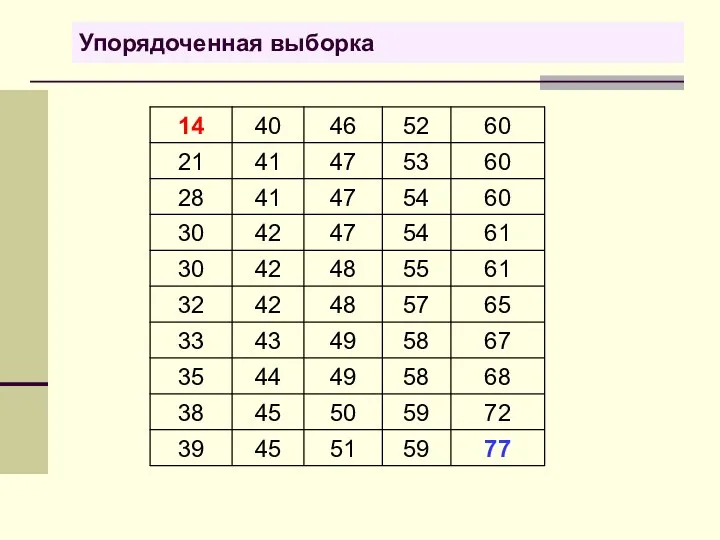
- 35. Упорядоченная выборка
- 36. Нахождение числа интервалов k и длины интервала h
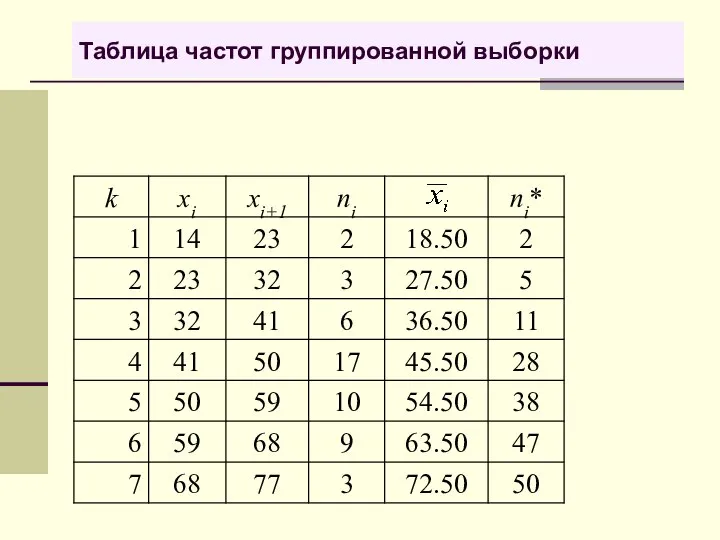
- 37. Таблица частот группированной выборки
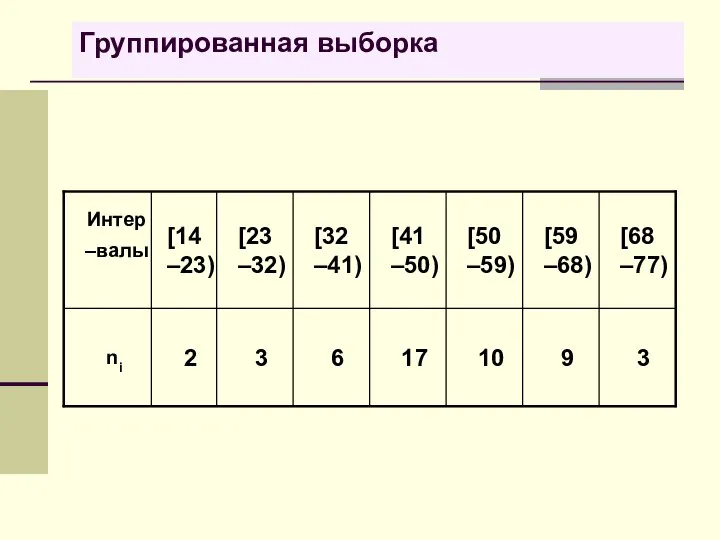
- 38. Группированная выборка
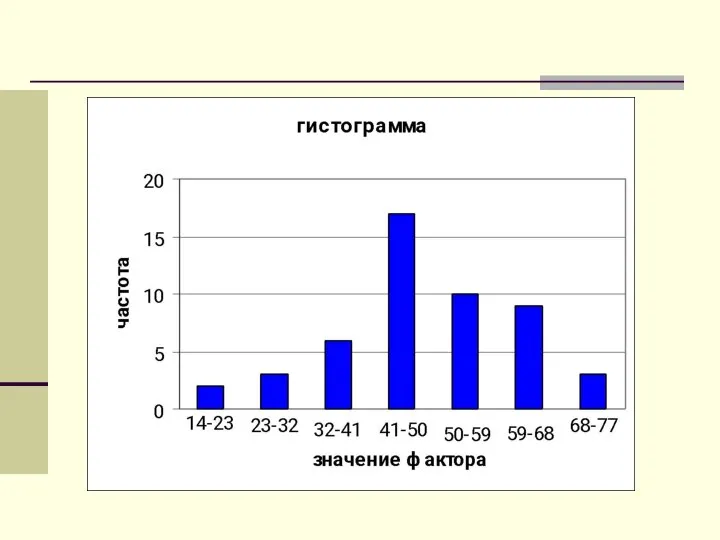
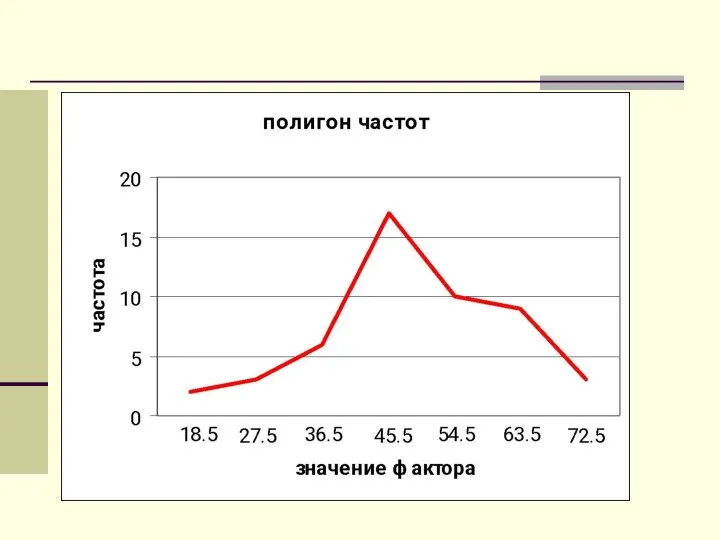
- 39. Графические характеристики выборки Если на каждом интервале построить прямоугольник с высотой ni/h, получим гистограмму. Кривая, соединяющая
- 40. Замечание Если по оси ординат откладываются высоты ni/h, то площадь ступенчатой фигуры под графиком гистограммы равна
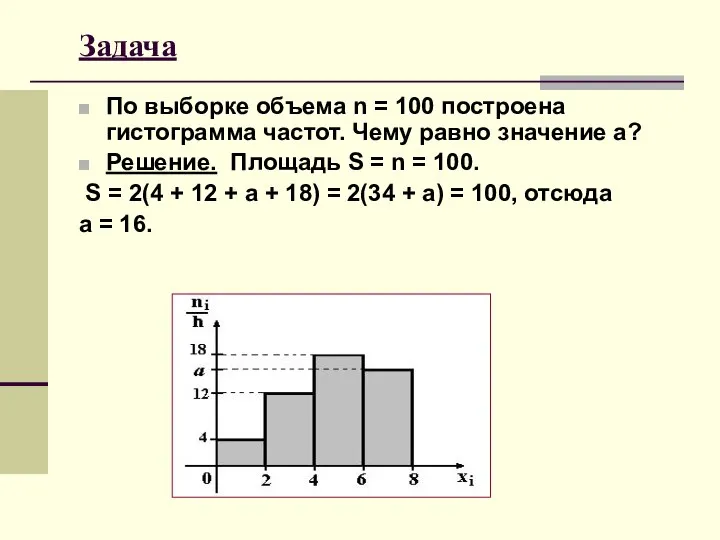
- 41. Задача По выборке объема n = 100 построена гистограмма частот. Чему равно значение а? Решение. Площадь
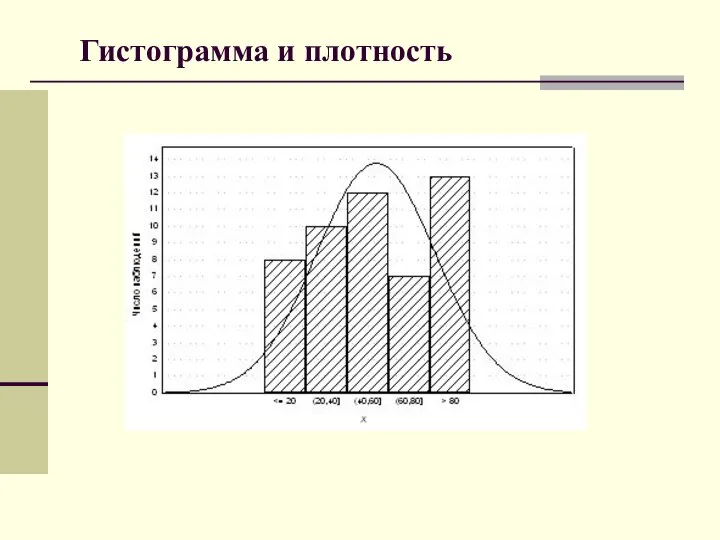
- 42. Смысл гистограммы и полигона При увеличении объема выборки и уменьшении интервала группировки гистограмма относительных частот является
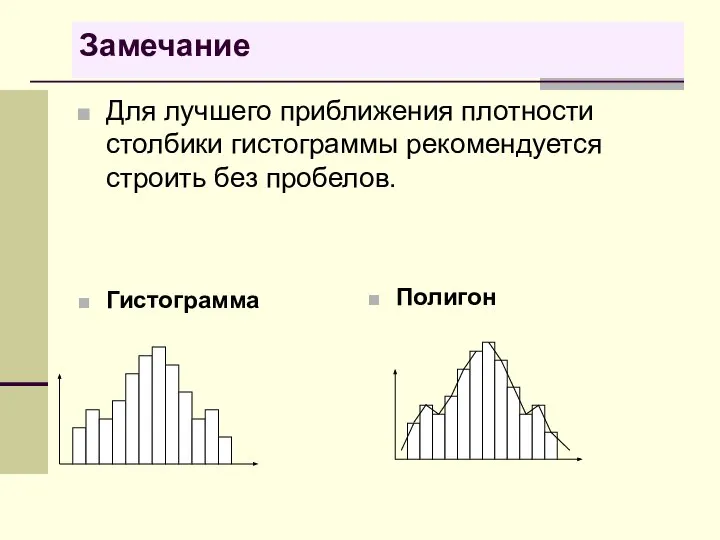
- 45. Замечание Для лучшего приближения плотности столбики гистограммы рекомендуется строить без пробелов. Гистограмма Полигон
- 46. Гистограмма и плотность
- 47. Кумулята Кумулята относительных частот – это ломаная, соединяющая точки с координатами (xi, ni*/n). Кумулята частот соединяет
- 49. Скачать презентацию


































 Траскрипция и трансляция
Траскрипция и трансляция ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АККРЕДИТАЦИИ
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АККРЕДИТАЦИИ Возникновение и развитие физической культуры
Возникновение и развитие физической культуры Классификация поверхностей
Классификация поверхностей Коммуникационная программа. Единое информационное пространство
Коммуникационная программа. Единое информационное пространство Презентация без названия
Презентация без названия МУНИЦИПАЛЬНОЕ ДОШКОЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ДЕТСКИЙ САД № 5 “РЯБИНКА” КОМБИНИРОВАННОГО ВИДА ГОРОДА КЫЗЫЛА Система контроля в ДОУ Составила старший воспитатель:
МУНИЦИПАЛЬНОЕ ДОШКОЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ДЕТСКИЙ САД № 5 “РЯБИНКА” КОМБИНИРОВАННОГО ВИДА ГОРОДА КЫЗЫЛА Система контроля в ДОУ Составила старший воспитатель:  Искусство кукольного театра
Искусство кукольного театра Приемка и хранение семечковых плодов
Приемка и хранение семечковых плодов  Некоторые популярные статистические критерии
Некоторые популярные статистические критерии Алгебра Алгебра Тема: «Свойства степени с натуральным показателем» Учитель Попова Ольга Николаевна
Алгебра Алгебра Тема: «Свойства степени с натуральным показателем» Учитель Попова Ольга Николаевна  Технология обслуживания проводником вагона бытовых узлов пассажирского вагона, связанных с системой водоснабжения
Технология обслуживания проводником вагона бытовых узлов пассажирского вагона, связанных с системой водоснабжения Анализ рисков
Анализ рисков Модернизация электропривода швейной машины челночной строчки
Модернизация электропривода швейной машины челночной строчки Soft Power Мягкая сила
Soft Power Мягкая сила Особенности выбора электрооборудования напряжением до 1000 В
Особенности выбора электрооборудования напряжением до 1000 В История развития прыжков в воду
История развития прыжков в воду Презентация____
Презентация____ Царствование Василия Шуйского
Царствование Василия Шуйского Самое-самое интересное о железной дороге
Самое-самое интересное о железной дороге Основы информационного права
Основы информационного права Разработка и моделирование неложных систем автоматизации с учетом специфики
Разработка и моделирование неложных систем автоматизации с учетом специфики Презентация Мониторинг отношений между сотрудниками таможенных органов как объект социльно-психологического мониторинга
Презентация Мониторинг отношений между сотрудниками таможенных органов как объект социльно-психологического мониторинга  Презентация по МХК Барельеф Изобразительное искусство.
Презентация по МХК Барельеф Изобразительное искусство. Аппаратные средства визуализации
Аппаратные средства визуализации Рецепт врача
Рецепт врача LXE10E Piping diagram
LXE10E Piping diagram Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений