Содержание
- 2. Постулаты квантовой физики Квантово-механические операторы Волновая функция Ψ(r,t) Уравнение Шредингера СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013
- 3. Постулат 1 -Существует некоторая комплексная функция Ψ(r,t)(1), наз. функцией состояния или волновой функцией механической системы, такая,
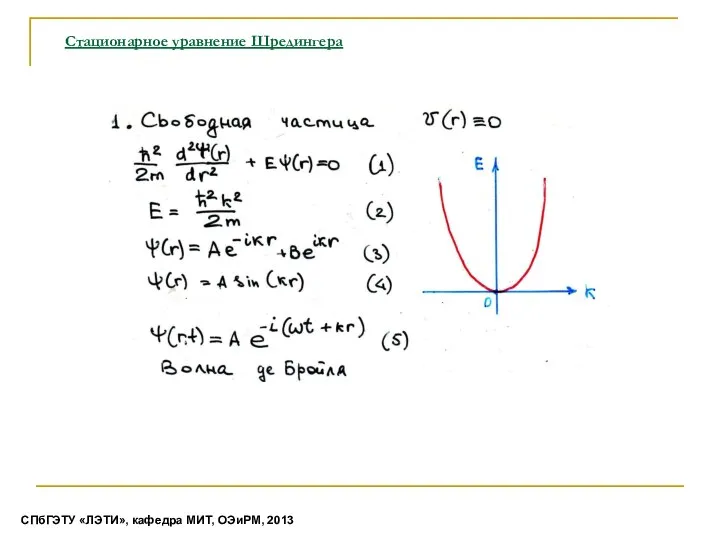
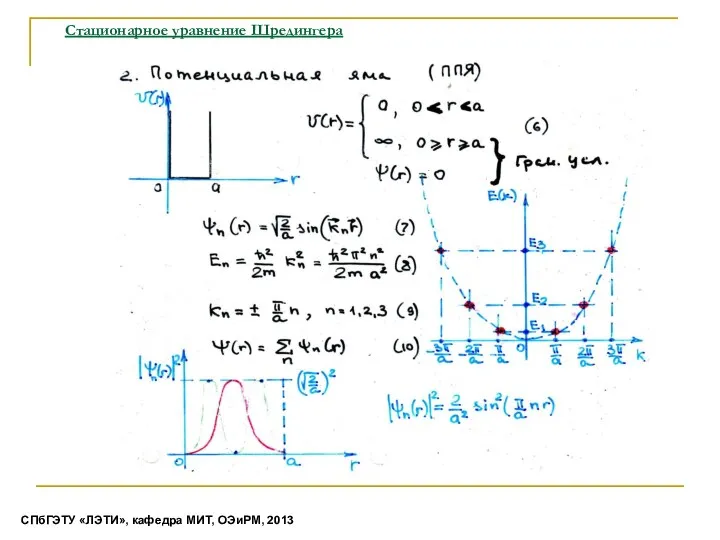
- 4. Стационарное уравнение Шредингера СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013
- 5. Стационарное уравнение Шредингера СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013
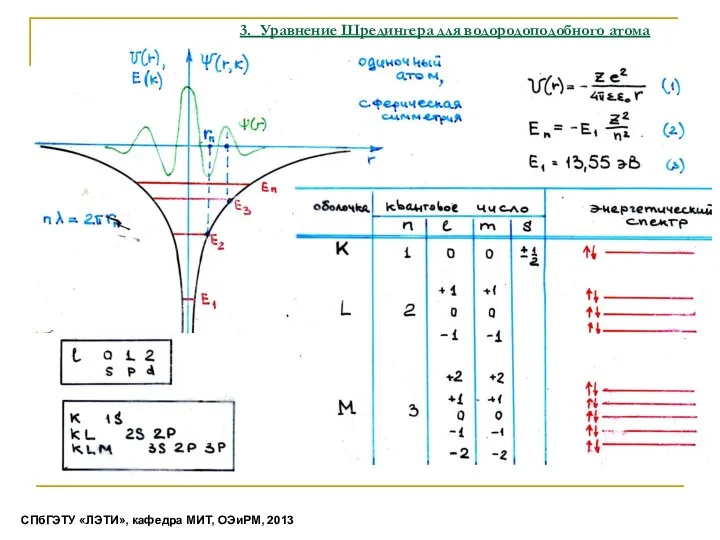
- 6. 3. Уравнение Шредингера для водородоподобного атома СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013
- 7. Тунне́льный эффект, туннели́рование — преодоление микрочастицей— преодоление микрочастицей потенциального барьера в случае, когда её полная энергия
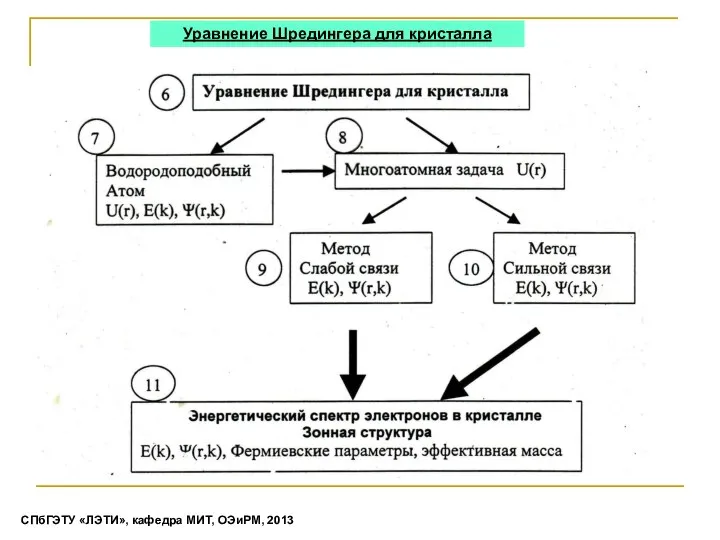
- 8. Уравнение Шредингера для кристалла СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013
- 9. Уравнение Шредингера для кристалла (постановка задачи) Методы решения: СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013
- 10. Методы решения: Уравнение Шредингера для кристалла (прдолжение) СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013
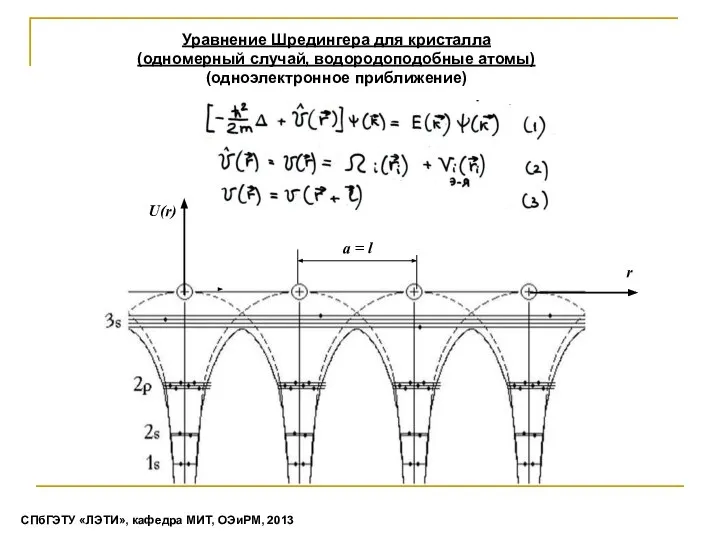
- 11. Уравнение Шредингера для кристалла (одномерный случай, водородоподобные атомы) (одноэлектронное приближение) СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013
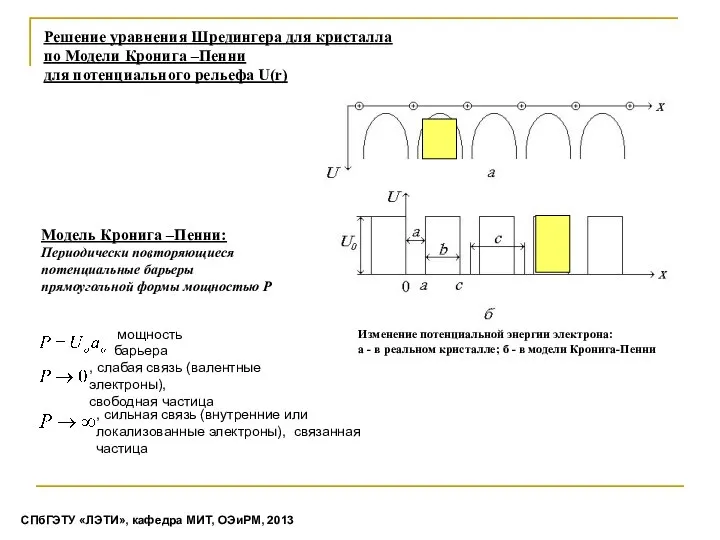
- 12. Модель Кронига –Пенни: Периодически повторяющиеся потенциальные барьеры прямоугольной формы мощностью Р Решение уравнения Шредингера для кристалла
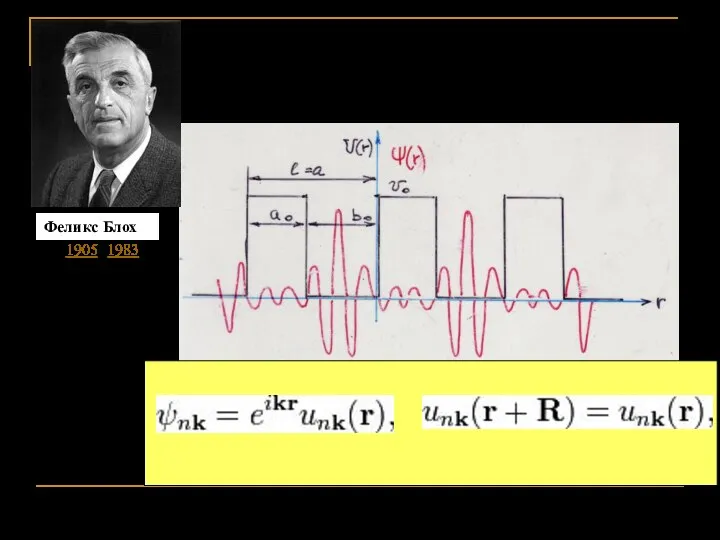
- 13. Теорема Блόха Нобелевская премия по физике 1952 г. СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013
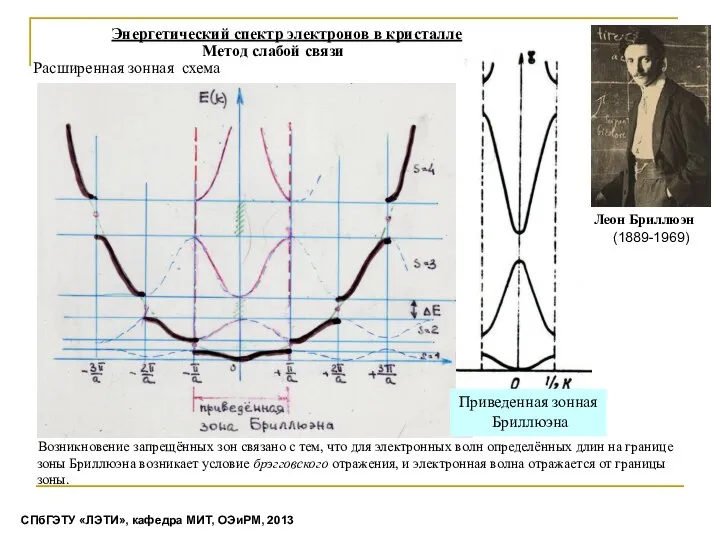
- 14. Расширенная зонная схема СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013 Приведенная зонная Бриллюэна (1889-1969) Леон Бриллюэн Возникновение
- 15. СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013
- 16. Влияние ограниченного размера кристалла Граничные условия Борна-Кармана: Ψ(x,y,z) = Ψ(x + a , y +b, z
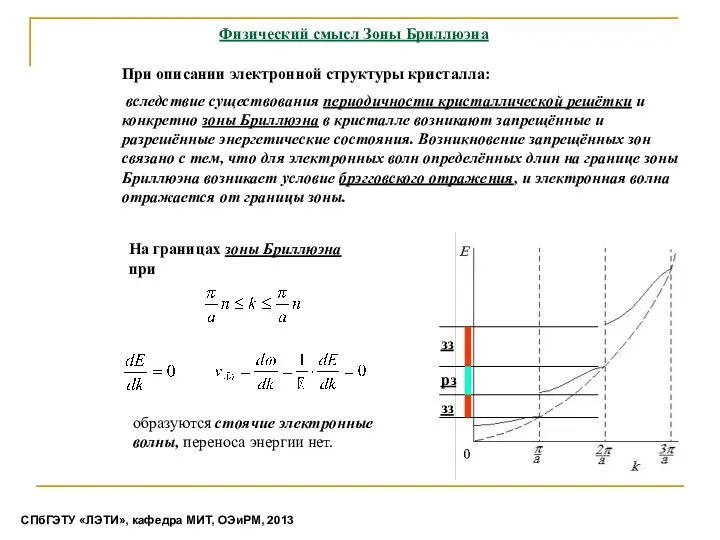
- 17. Физический смысл Зоны Бриллюэна При описании электронной структуры кристалла: вследствие существования периодичности кристаллической решётки и конкретно
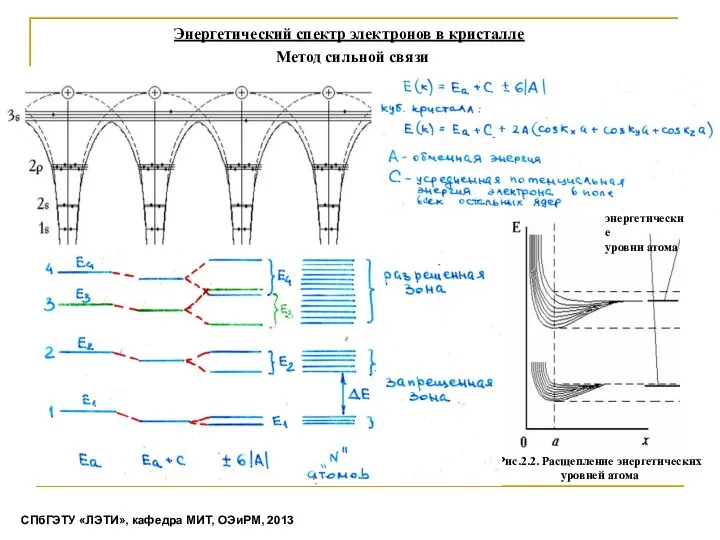
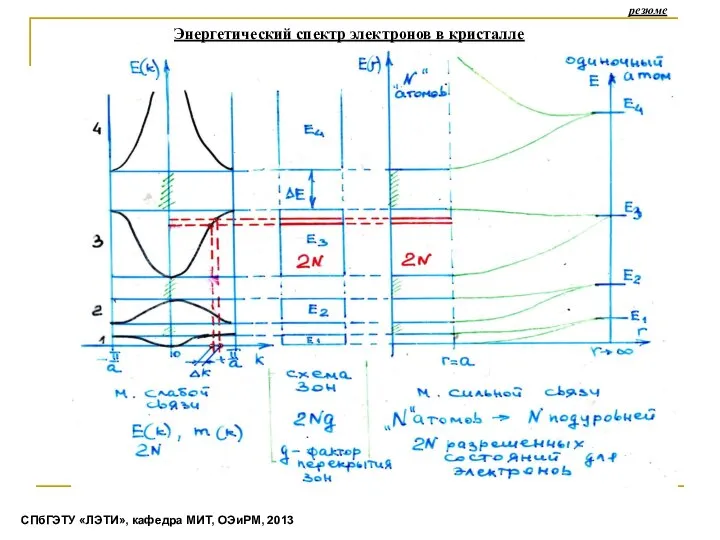
- 18. Энергетический спектр электронов в кристалле резюме СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013
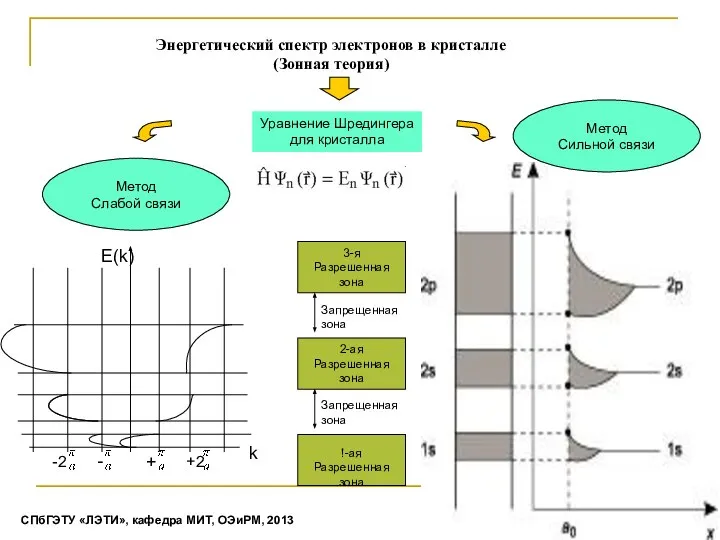
- 19. Уравнение Шредингера для кристалла Метод Слабой связи Метод Сильной связи Энергетический спектр электронов в кристалле (Зонная
- 20. Прямое пространство Конфигурационное [м] Обратное пространство Волновое [1/м] СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2013 Базисные вектора
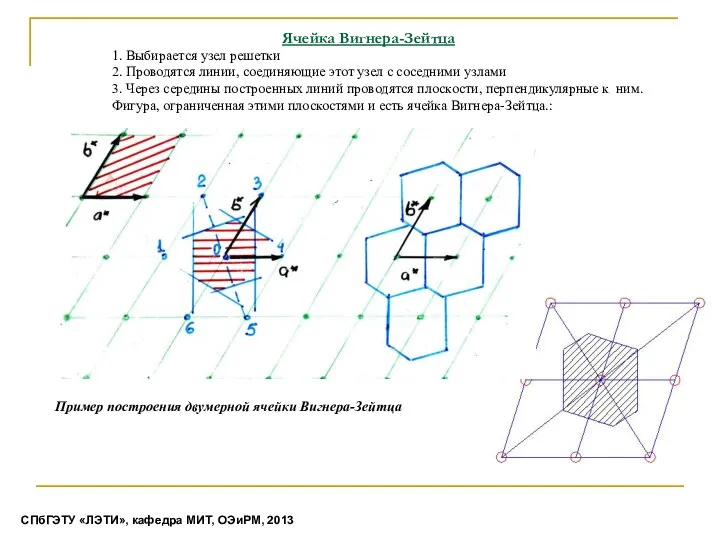
- 21. Ячейка Вигнера-Зейтца 1. Выбирается узел решетки 2. Проводятся линии, соединяющие этот узел с соседними узлами 3.
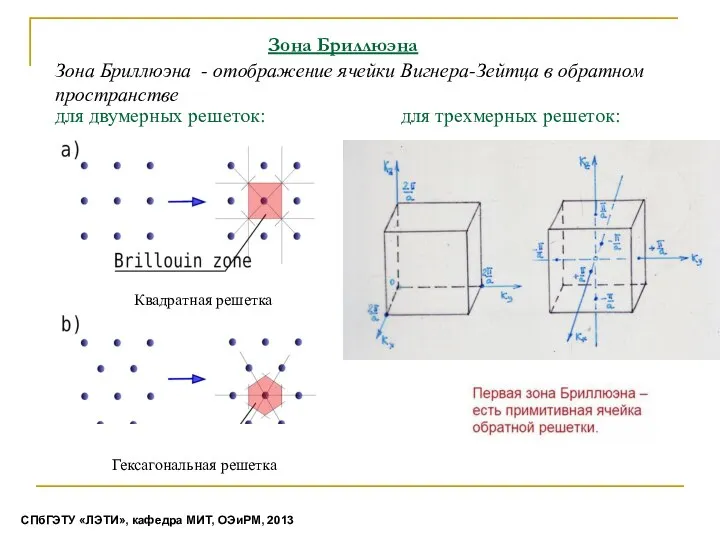
- 22. Зона Бриллюэна Квадратная решетка Гексагональная решетка для двумерных решеток: Зона Бриллюэна - отображение ячейки Вигнера-Зейтца в
- 23. Условие Вульфа — Брэгга определяет направление максимумов дифракции упруго рассеянного на кристалле рентгеновского излучения. Выведено в
- 24. Практическое использование концепции зон Броиллюэна В дифракции : на кристаллической решётке дифрагируют только те лучи, волновой
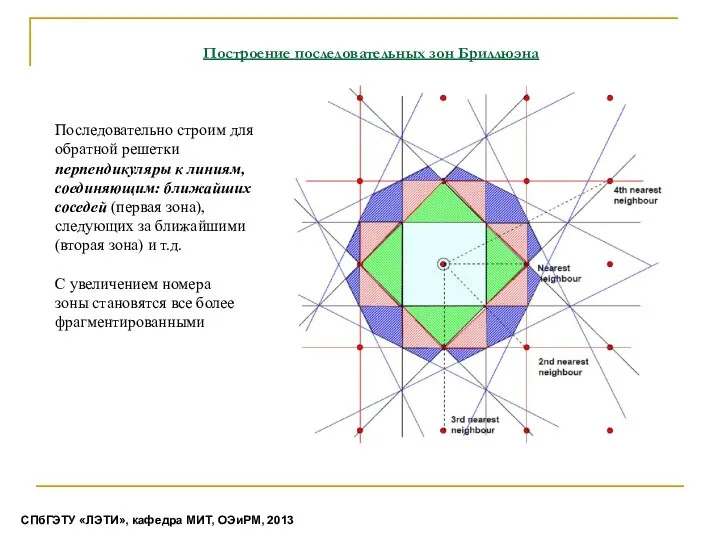
- 25. Построение последовательных зон Бриллюэна Последовательно строим для обратной решетки перпендикуляры к линиям, соединяющим: ближайших соседей (первая
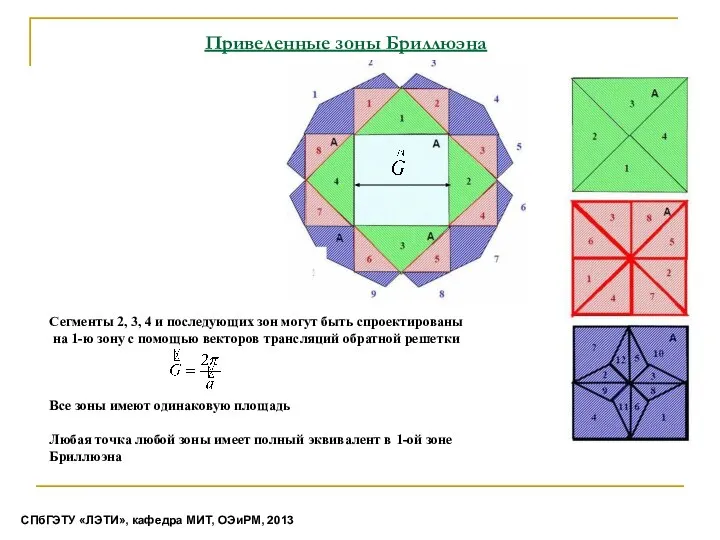
- 26. Приведенные зоны Бриллюэна СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013
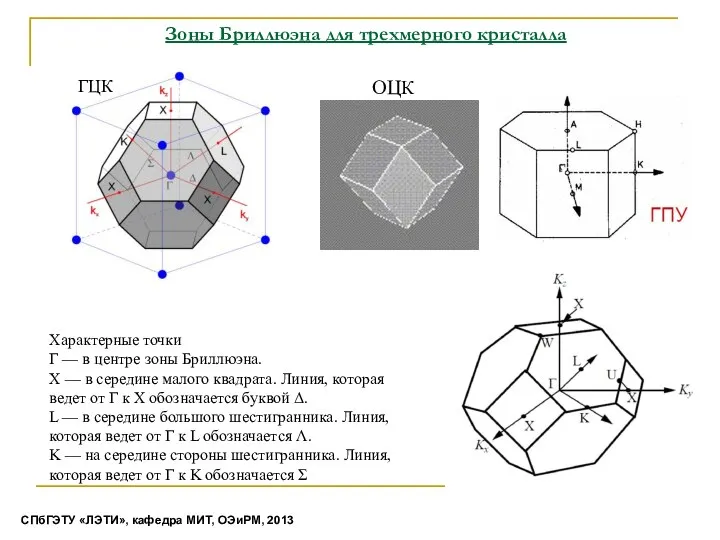
- 27. Зоны Бриллюэна для трехмерного кристалла Характерные точки Γ — в центре зоны Бриллюэна. X — в
- 29. Скачать презентацию






![Прямое пространство Конфигурационное [м] Обратное пространство Волновое [1/м] СПбГЭТУ «ЛЭТИ», кафедра](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301922/slide-19.jpg)


 Типовые критерии отнесения товаров к группам риска и применяемые формы таможенного контроля Подготовили: Студентки 5 курса, Груп
Типовые критерии отнесения товаров к группам риска и применяемые формы таможенного контроля Подготовили: Студентки 5 курса, Груп Системы документации
Системы документации Кадровая политика организации
Кадровая политика организации Профессиональная культура учителя
Профессиональная культура учителя Гражданское общество: основные параметры и характеристики Выполнила: Рассолова Олеся группа: Т082
Гражданское общество: основные параметры и характеристики Выполнила: Рассолова Олеся группа: Т082 Европейский Союз Мировая экономика
Европейский Союз Мировая экономика МБОУ СОШ №16 г.Балаково Саратовской области.
МБОУ СОШ №16 г.Балаково Саратовской области. Критерии успешности учителя, воспитателя
Критерии успешности учителя, воспитателя Көшбасшы және көшбасшылық
Көшбасшы және көшбасшылық Поражение СОПР
Поражение СОПР HTML и CSS. CSS. (Лекция 5)
HTML и CSS. CSS. (Лекция 5) Понятие потоков ввода/вывода
Понятие потоков ввода/вывода СТО с участком диагностики двигателя
СТО с участком диагностики двигателя Как стать бухгалтером с нуля. Программа вебинара
Как стать бухгалтером с нуля. Программа вебинара Церковь Великого Устюга Спасо-Преображенская
Церковь Великого Устюга Спасо-Преображенская Чистый подход для тренеров
Чистый подход для тренеров Турфирма «Невская Ривьера». Романтические отношения в разных странах
Турфирма «Невская Ривьера». Романтические отношения в разных странах Автоматические трансмиссии
Автоматические трансмиссии Группа разработки финансовых мер по борьбе с отмыванием денег
Группа разработки финансовых мер по борьбе с отмыванием денег Господь - Пастырь мой
Господь - Пастырь мой Выпуклый анализ. Пространство подмножеств. Лекция 2
Выпуклый анализ. Пространство подмножеств. Лекция 2 Совершенствование государственной политики в сфере дорожного хозяйства Кемеровской области
Совершенствование государственной политики в сфере дорожного хозяйства Кемеровской области Язык SMS. Специфика письменного печатного общения
Язык SMS. Специфика письменного печатного общения НЕПОСЕДА – ВЕТЕРОК (учимся образовывать относительные прилагательные) Составила: учитель-логопед д/с 56 ОАО «РЖД» Власенкова
НЕПОСЕДА – ВЕТЕРОК (учимся образовывать относительные прилагательные) Составила: учитель-логопед д/с 56 ОАО «РЖД» Власенкова  5 основных стилей в одежде - от авангарда до классики
5 основных стилей в одежде - от авангарда до классики Об утверждении положения о порядке реализации правотворческой инициативы граждан в муниципальном образовании "Северодвинск&quo
Об утверждении положения о порядке реализации правотворческой инициативы граждан в муниципальном образовании "Северодвинск&quo Алгоритмы на тему «Графы»
Алгоритмы на тему «Графы» №1.Какие права принадлежат собственнику? 1) владение; 2) пользование; 3) распоряжение; 4) все перечисленные права;
№1.Какие права принадлежат собственнику? 1) владение; 2) пользование; 3) распоряжение; 4) все перечисленные права;