Содержание
- 2. Поверхность – это совокупность всех последовательных положений некоторой перемещающейся в пространстве линии Красовская Н.И.
- 3. Способы образования и задания поверхностей. Каркас поверхности. Определитель поверхности Красовская Н.И.
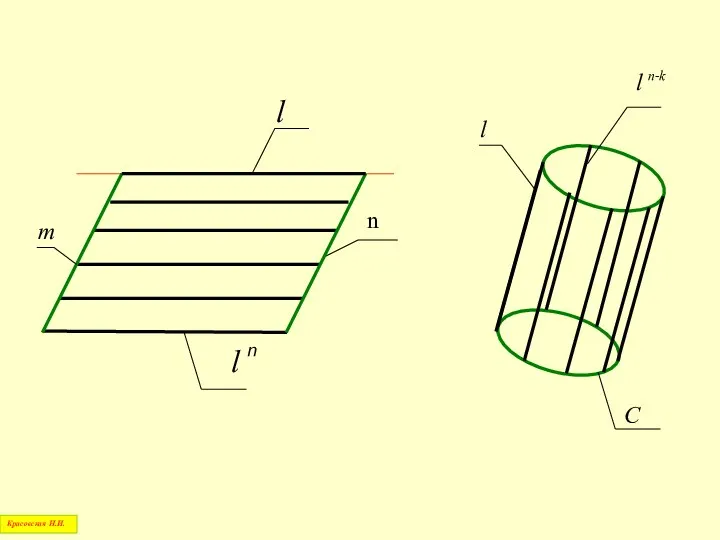
- 4. Движущаяся в процессе образования поверхности линия называется образующей Линия, по которой скользит образующая, называется направляющей Красовская
- 5. l m n C l n Красовская Н.И.
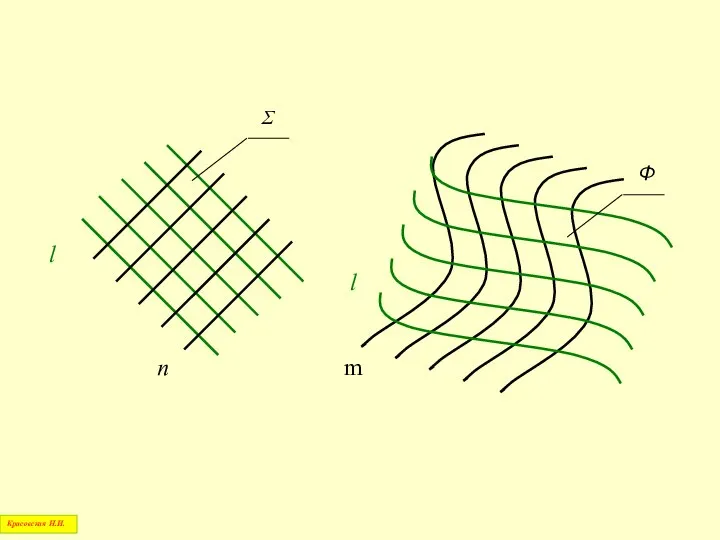
- 6. Совокупность намеченных на поверхности образующих и направляющих линий называется линейным каркасом поверхности Красовская Н.И.
- 7. l l n m Красовская Н.И.
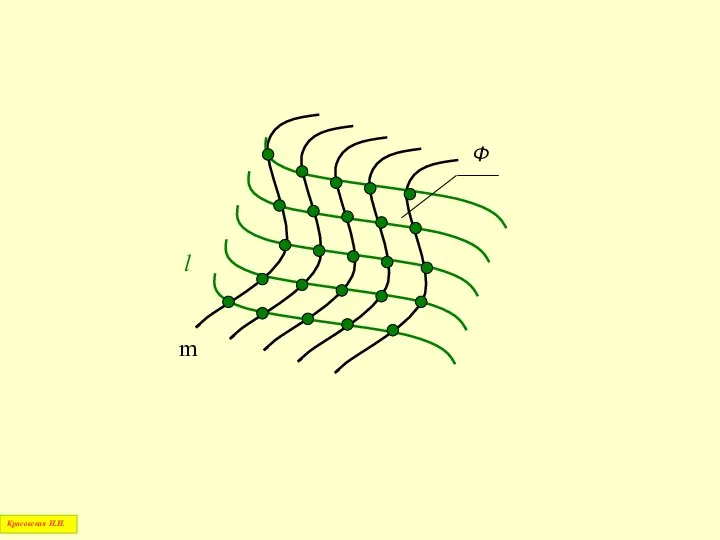
- 8. Совокупность точек на поверхности, выбранных таким образом, чтобы, ориентируясь по ним, можно достаточно полно представить форму
- 9. l m Красовская Н.И.
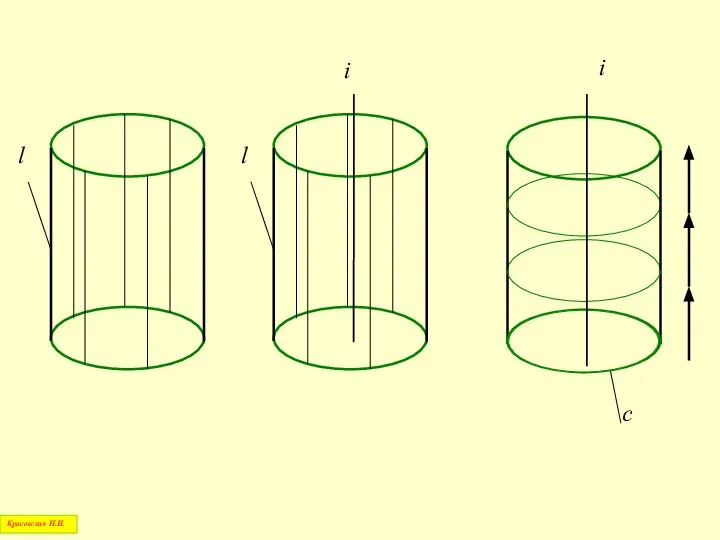
- 10. i i c l l Красовская Н.И.
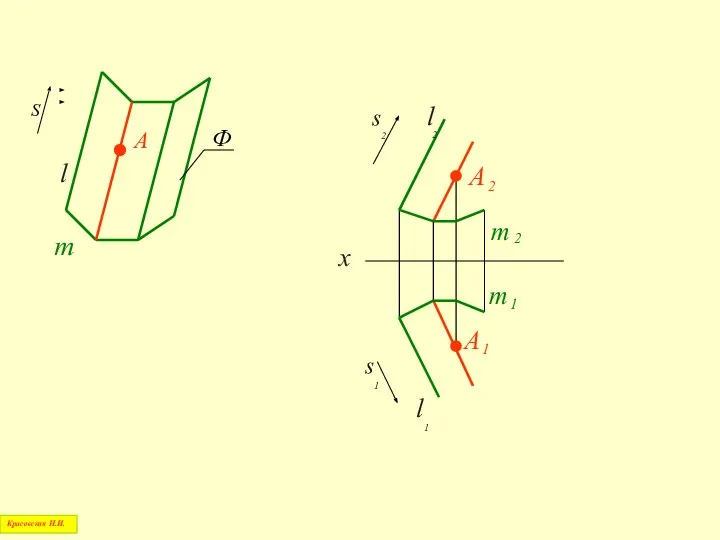
- 11. Совокупность независимых условий, однозначно задающих поверхность, называется её определителем Ф(l,i)[A] Красовская Н.И.
- 12. s m S l m l а) б) Красовская Н.И. Ф(l,m)[A] Ф(l,m)[A]
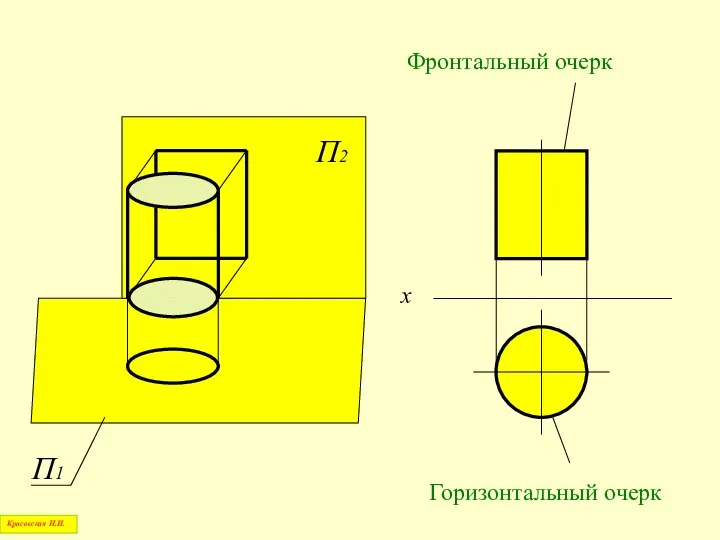
- 13. Очерк поверхности Красовская Н.И.
- 14. Очерк поверхности при ортогональном проецировании – это линия, ограничивающая проекцию поверхности на плоскостях проекций Красовская Н.И.
- 15. П1 П2 х Красовская Н.И.
- 16. Классификация поверхностей Красовская Н.И.
- 17. По виду образующей все поверхности можно разделить на линейчатые и нелинейчатые Красовская Н.И.
- 18. У линейчатых поверхностей образующей является прямая линия, у нелинейчатых – кривая линия Красовская Н.И.
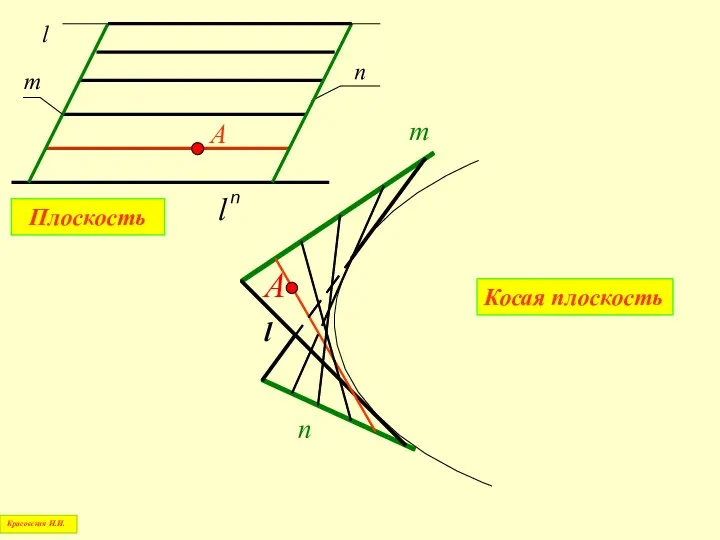
- 19. Линейчатые поверхности Красовская Н.И.
- 20. Плоскость l m n n А Красовская Н.И. Косая плоскость m n А l
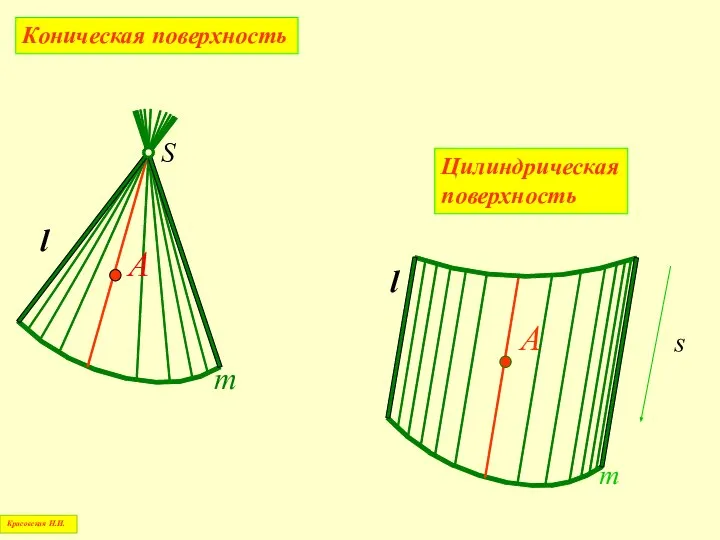
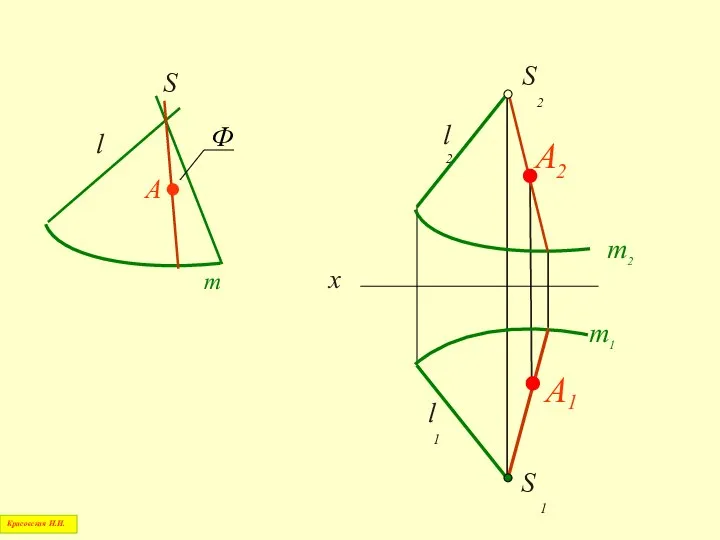
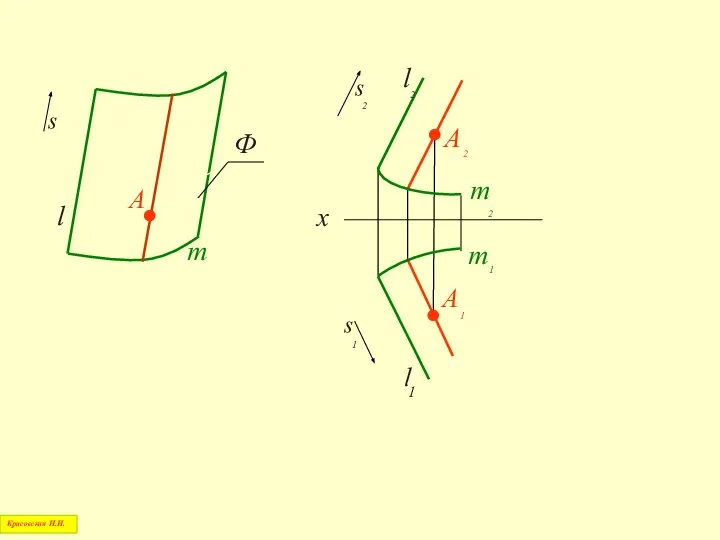
- 21. Коническая поверхность m S А l Красовская Н.И. Цилиндрическая поверхность m А l s
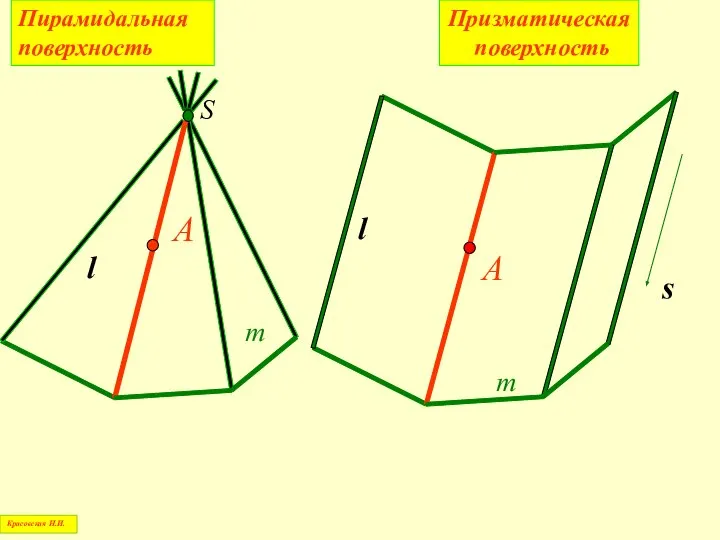
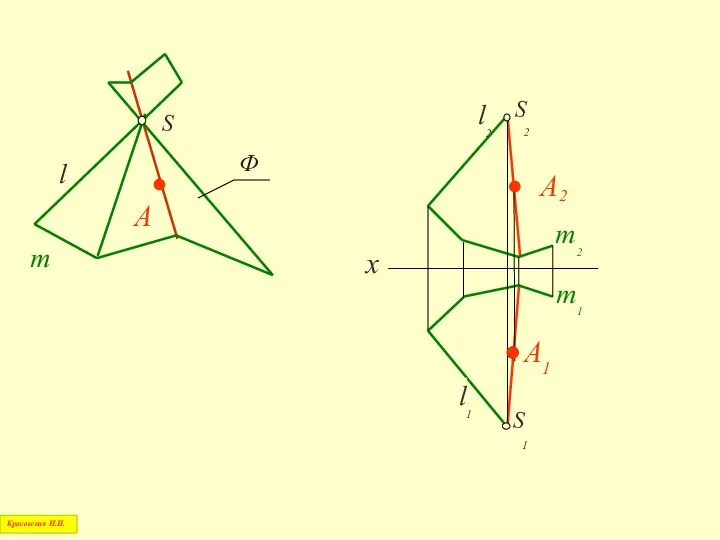
- 22. Пирамидальная поверхность m S А l Красовская Н.И. Призматическая поверхность m А l s
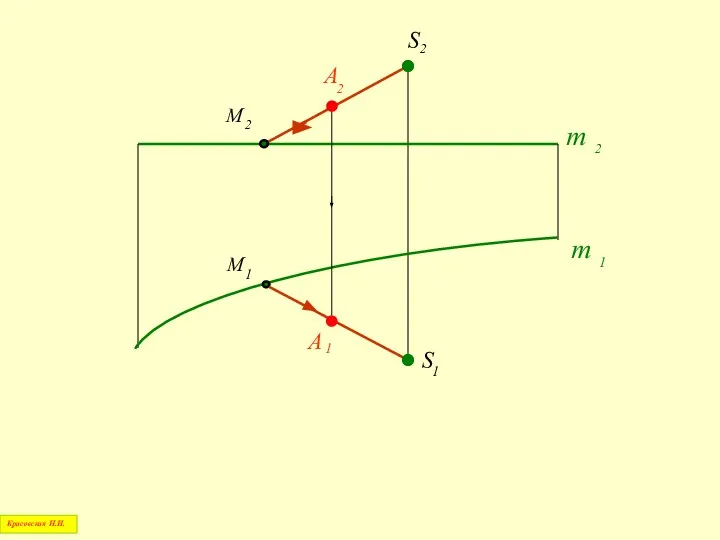
- 23. Точка принадлежит поверхности, если она лежит на какой – нибудь линии этой поверхности Красовская Н.И. Линия
- 24. Красовская Н.И.
- 25. 1. Через заданную проекцию точки, лежащей на поверхности, проводится проекция простейшей линии, принадлежащей этой поверхности 3.
- 26. S S 1 2 x m2 m1 m l S А Красовская Н.И.
- 27. s s m m x 2 1 1 2 s l A m Красовская Н.И.
- 28. S m x m S 1 2 1 2 l A m S Красовская Н.И.
- 29. S Ф s x 1 m l А Красовская Н.И.
- 30. Таким образом, через каждую точку линейчатой поверхности можно всегда провести прямую линию Красовская Н.И.
- 31. Многогранники Красовская Н.И.
- 32. Многогранник – замкнутая пространственная фигура, ограниченная плоскими многоугольниками Красовская Н.И.
- 33. Если все вершины и ребра многогранника находятся по одну сторону плоскости любой его грани, то многогранник
- 34. Правильные многогранники – это фигуры, у которых все грани являются правильными и конгруэнтными многоугольниками, а многогранные
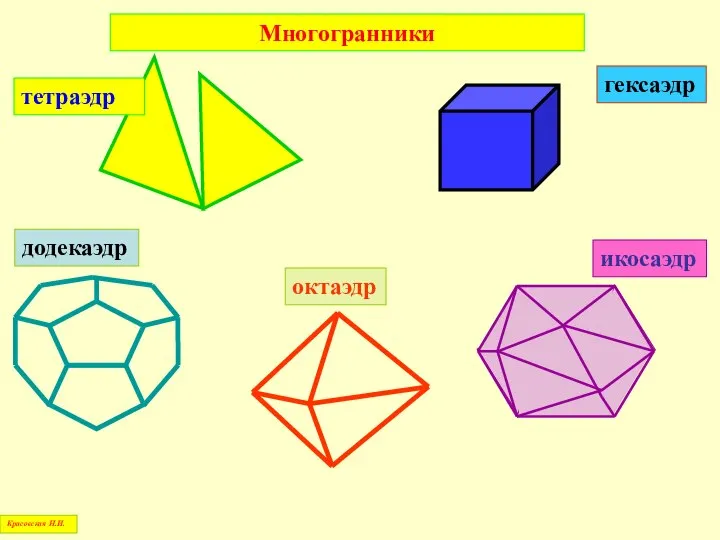
- 35. Правильными многогранниками являются: тетраэдр – правильный четырехгранник, гексаэдр – правильный шестигранник, октаэдр – правильный восьмигранник, додекаэдр
- 36. тетраэдр гексаэдр октаэдр додекаэдр икосаэдр Многогранники Красовская Н.И.
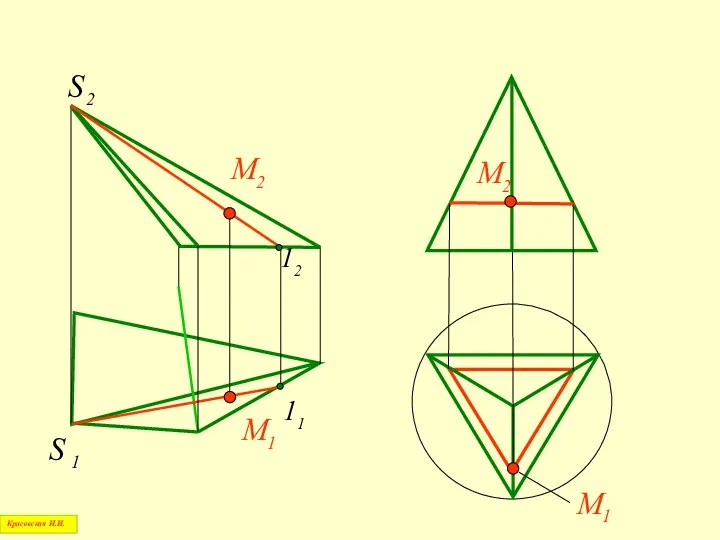
- 37. Пирамида – это многогранник, одна грань которого – многоугольник, а остальные – треугольники с общей вершиной
- 38. Правильная пирамида – это пирамида, у которой основание является правильным многоугольником, а высота проходит через центр
- 39. 12 11 Красовская Н.И.
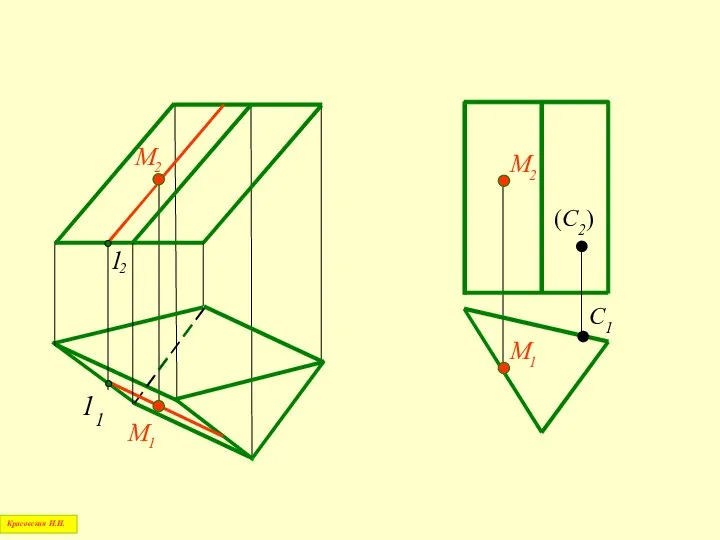
- 40. Призма – это многогранник, две грани которого представляют собой равные многоугольники с взаимно параллельными сторонами, а
- 41. Прямая призма – призма, ребра которой перпендикулярны к плоским основаниям Красовская Н.И.
- 42. 11 (С2) С1 Красовская Н.И.
- 43. Поверхности вращения Красовская Н.И.
- 44. У поверхности вращения геометрическая часть определителя состоит из образующей l и оси вращения i: Ф (l,i)[A]
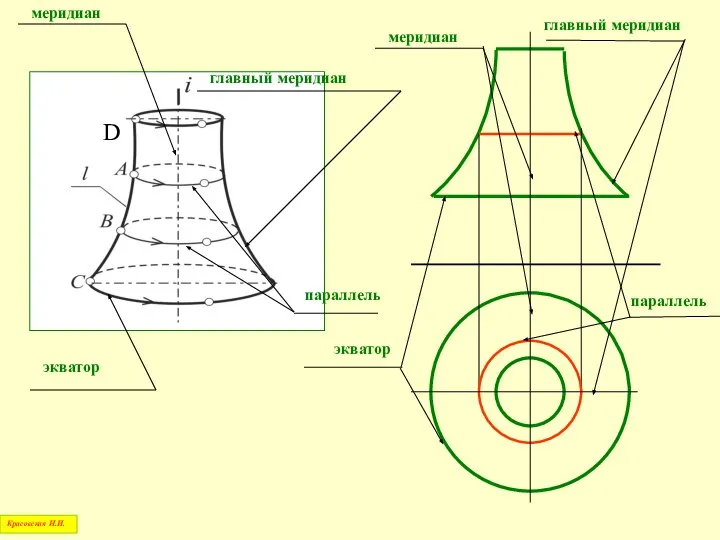
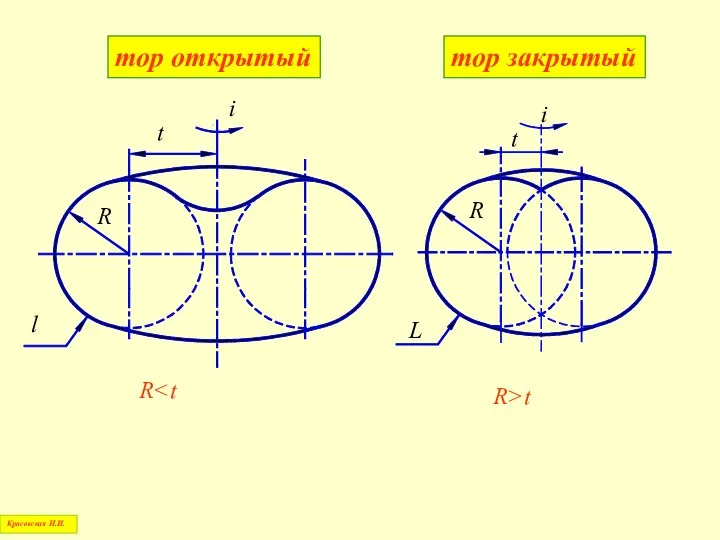
- 45. Плоскости, перпендикулярные к оси вращения, пересекают поверхность по окружностям, которые называются параллелями Радиус каждой параллели измеряется
- 46. Наибольшую из параллелей называют экватором, наименьшую – горлом Красовская Н.И.
- 47. Плоскость, проходящая через ось поверхности вращения, называется меридиональной, а линия пересечения поверхности с этой плоскостью называется
- 48. Если меридиональная плоскость параллельна фронтальной плоскости проекций П2, то в сечении получается меридиан, который называется главным
- 49. D Красовская Н.И.
- 51. Примеры поверхностей вращения Красовская Н.И.
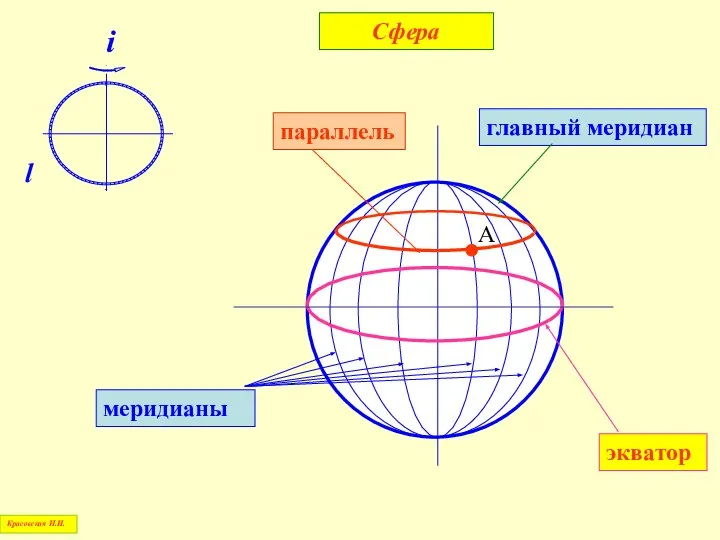
- 52. A главный меридиан экватор параллель меридианы Сфера i l Красовская Н.И.
- 53. видео
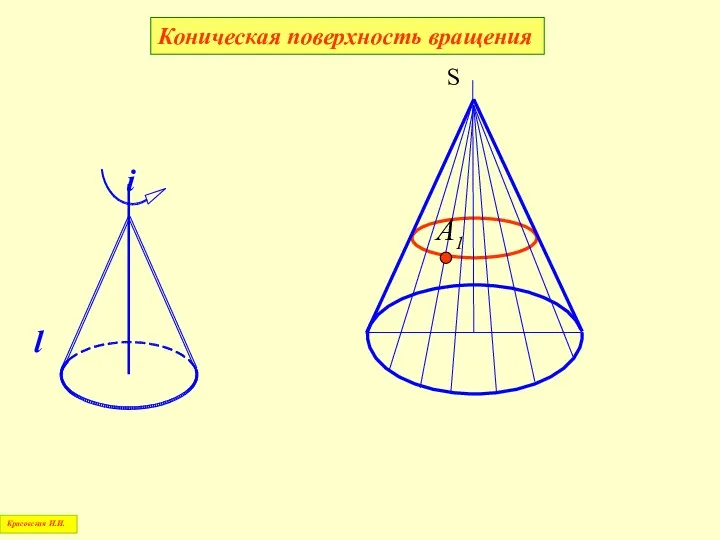
- 54. S Коническая поверхность вращения l Красовская Н.И.
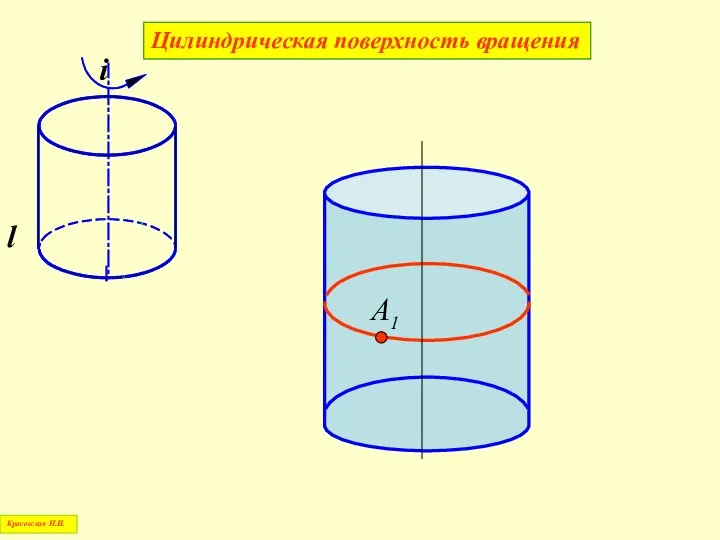
- 56. А 1 Цилиндрическая поверхность вращения Красовская Н.И.
- 58. Красовская Н.И.
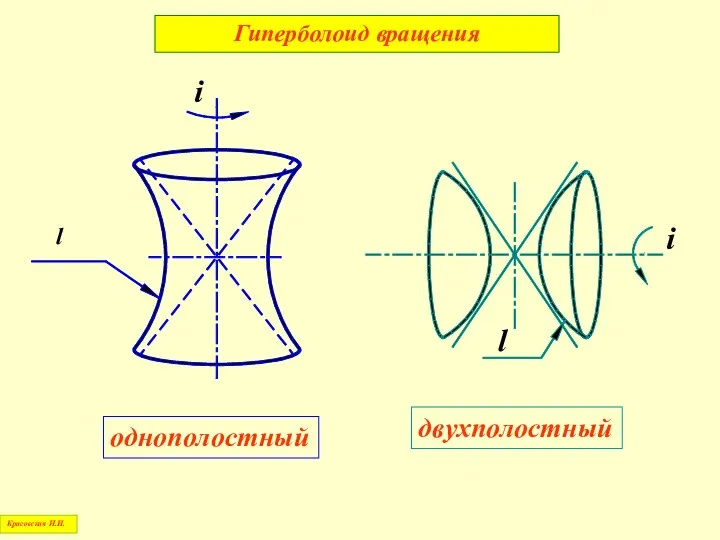
- 61. Гиперболоид вращения Красовская Н.И.
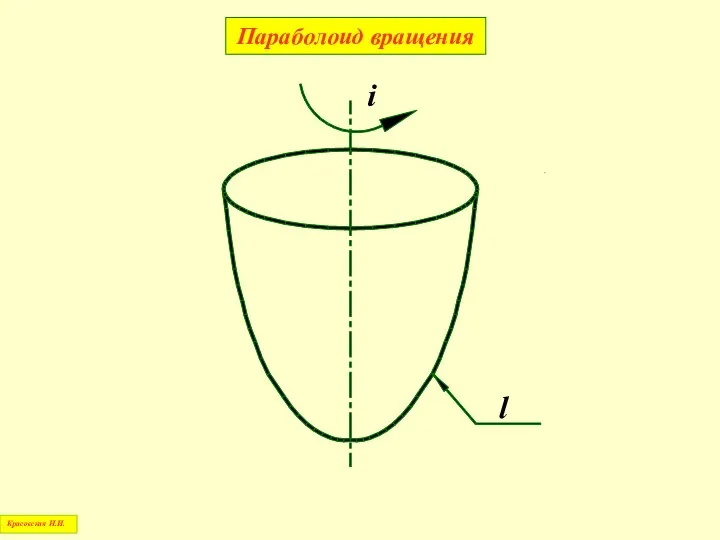
- 62. Параболоид вращения Красовская Н.И.
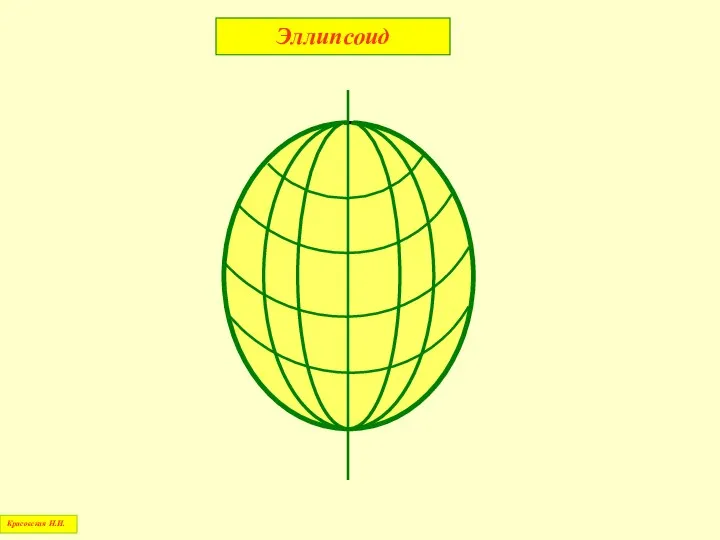
- 63. Эллипсоид Красовская Н.И.
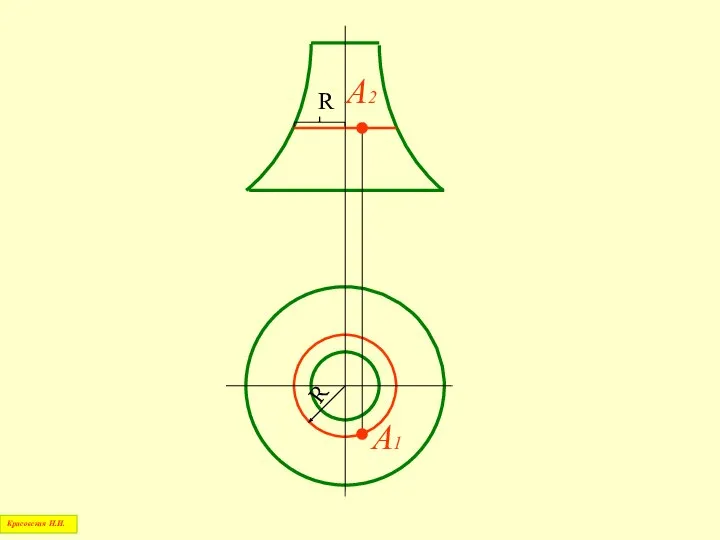
- 64. R R A1 A2 Красовская Н.И.
- 65. 3. По линии проекционной связи на построенной проекции параллели находят недостающую проекцию точки с учетом ее
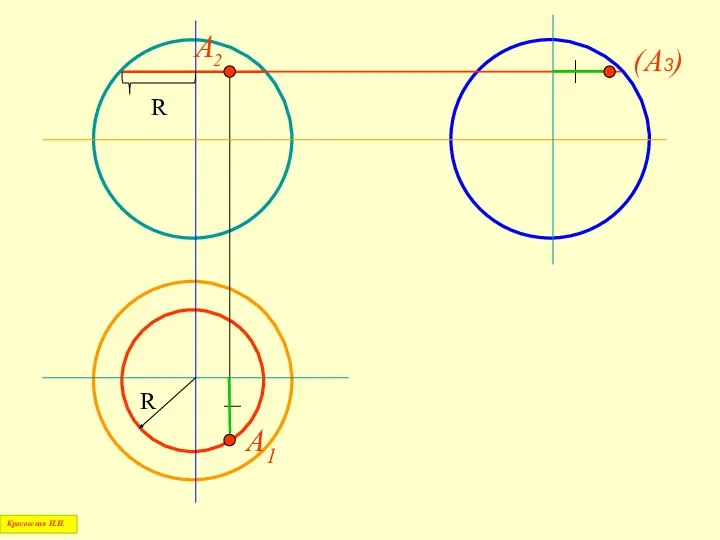
- 66. Построение точки на поверхности сферы Красовская Н.И.
- 67. А1 (А3) Красовская Н.И.
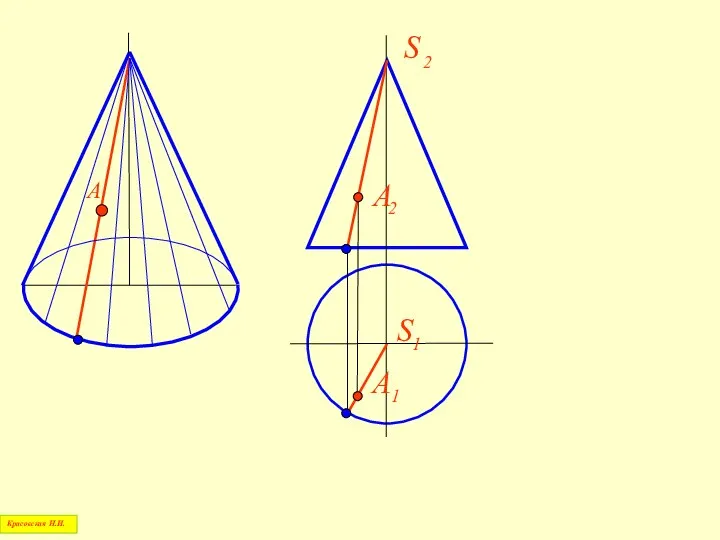
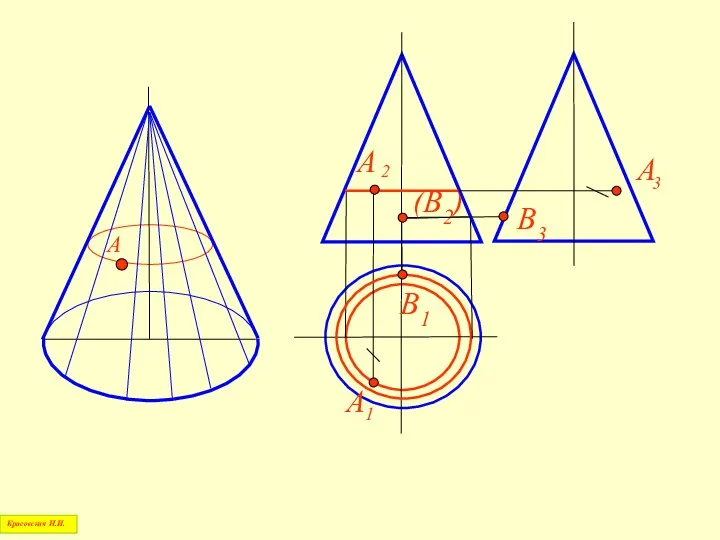
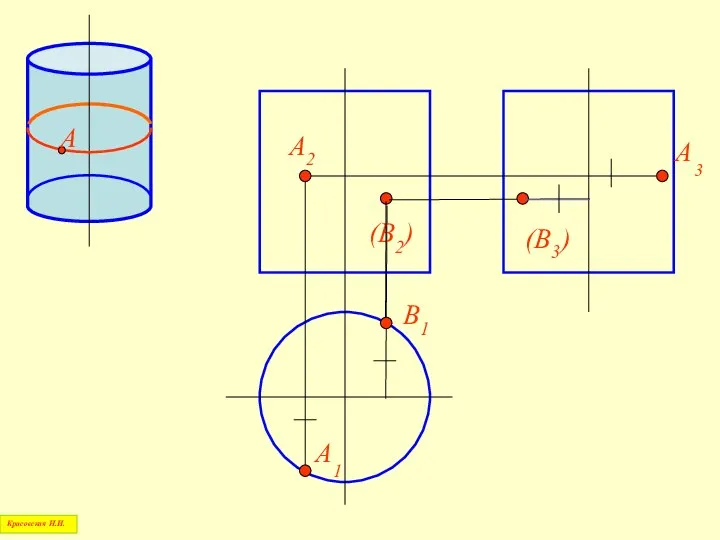
- 68. Построение точки на поверхности прямого кругового конуса Красовская Н.И.
- 69. А Красовская Н.И.
- 70. А Красовская Н.И. (В2) В1 В3
- 71. Построение точки на поверхности прямого кругового цилиндра Красовская Н.И.
- 72. А2 Красовская Н.И. (В2) В1 (В3)
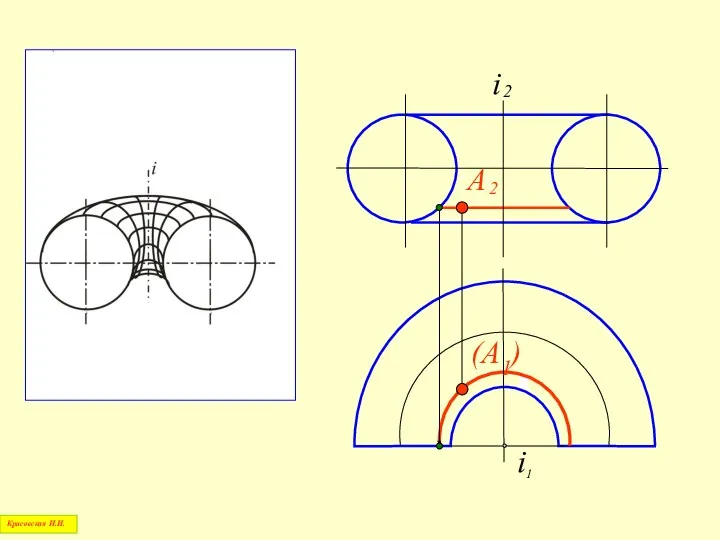
- 73. Т О Р Красовская Н.И.
- 74. i 2 i 1 (А1) Красовская Н.И.
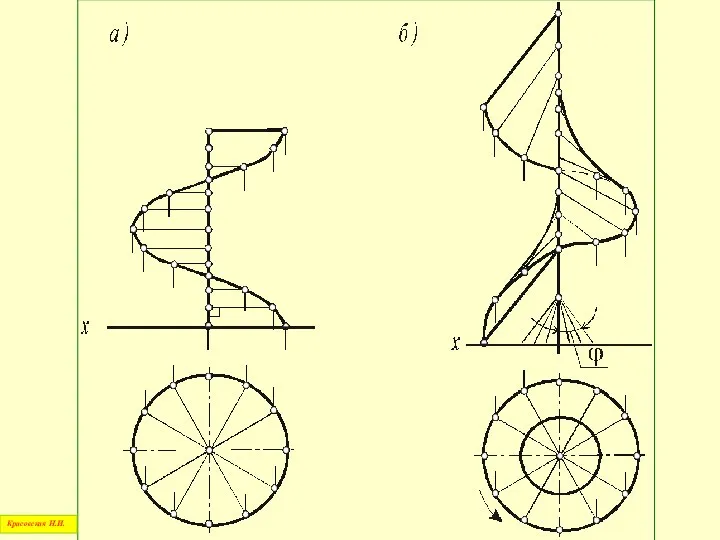
- 75. Винтовые поверхности Красовская Н.И.
- 76. Все точки винтовой поверхности совершают винтовые движения, описывая винтовые линии – гелисы, а поверхности называются геликоидами
- 77. Прямые геликоиды, если угол наклона образующей равен 90° Наклонные - если угол не равен 90° Красовская
- 78. Красовская Н.И.
- 79. - поверхность может быть получена вращением некоторой образующей вокруг оси или движением ее по направляющей -
- 81. Скачать презентацию





![Совокупность независимых условий, однозначно задающих поверхность, называется её определителем Ф(l,i)[A] Красовская Н.И.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1313395/slide-10.jpg)
![s m S l m l а) б) Красовская Н.И. Ф(l,m)[A] Ф(l,m)[A]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1313395/slide-11.jpg)








































 Грибы Магаданской области - презентация для начальной школы_
Грибы Магаданской области - презентация для начальной школы_ АВС инфузионной терапии
АВС инфузионной терапии  Биохимия гормонов Механизм действия гормонов белковой и пептидной природы
Биохимия гормонов Механизм действия гормонов белковой и пептидной природы Червячная передача
Червячная передача Презентация "Создание интернет магазина" - скачать презентации по Экономике
Презентация "Создание интернет магазина" - скачать презентации по Экономике Презентация "Покупательское поведение на рынках" - скачать презентации по Экономике
Презентация "Покупательское поведение на рынках" - скачать презентации по Экономике My Idol Ronaldinho
My Idol Ronaldinho Разминка по теме: Правление Петра I Работу выполнил: студент 1-го курса группы ЮБ 02/1402 Куликов Андрей
Разминка по теме: Правление Петра I Работу выполнил: студент 1-го курса группы ЮБ 02/1402 Куликов Андрей  Презентация На тему : « Рынок труда, его особенности и механизм функционирования» Цель: Раскрыть понятие Рынок труда, описать его
Презентация На тему : « Рынок труда, его особенности и механизм функционирования» Цель: Раскрыть понятие Рынок труда, описать его  В.Г.Короленко. Слово о писателе. «В дурном обществе»
В.Г.Короленко. Слово о писателе. «В дурном обществе» Проект воспитательной системы 12 – летнего образования в школе
Проект воспитательной системы 12 – летнего образования в школе Принцип работы асинхронных вентильных каскадов
Принцип работы асинхронных вентильных каскадов Бизнес-идея. Шаблон
Бизнес-идея. Шаблон Дисциплина профессионального цикла для студентов, обучающихся по магистерским программам
Дисциплина профессионального цикла для студентов, обучающихся по магистерским программам  Кривошипно-шатунный механизм двигателя
Кривошипно-шатунный механизм двигателя Обработка списков в программах на языке Пролог. Множества
Обработка списков в программах на языке Пролог. Множества Основные положения по проектированию механосборочного производства (часть 2)
Основные положения по проектированию механосборочного производства (часть 2) Тема 10. Управление основным капиталом предприятия.
Тема 10. Управление основным капиталом предприятия.  Методы очистки природных и сточных вод
Методы очистки природных и сточных вод ВКР. Методика развития координационных способностей у синхронисток 13-15 лет
ВКР. Методика развития координационных способностей у синхронисток 13-15 лет Дружба крепкая не сломается…
Дружба крепкая не сломается… Релігія Давнього Китаю конфуціанство
Релігія Давнього Китаю конфуціанство Физика среды и ограждающие конструкции
Физика среды и ограждающие конструкции Программируемое реле ПР 110
Программируемое реле ПР 110 Кривые спроса и общего дохода для отдельной фирмы в условиях совершенной конкуренции
Кривые спроса и общего дохода для отдельной фирмы в условиях совершенной конкуренции Национальный исследовательский Томский политехнический университет Институт инженерного предпринимательства Управление пе
Национальный исследовательский Томский политехнический университет Институт инженерного предпринимательства Управление пе 11_UP_Kouch.pptx
11_UP_Kouch.pptx С головы до пят мужчины
С головы до пят мужчины